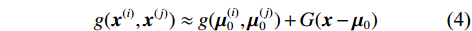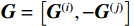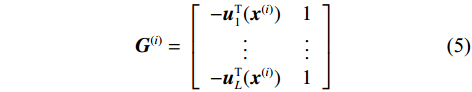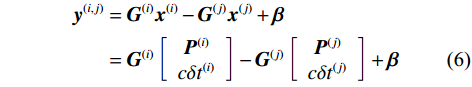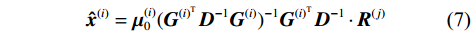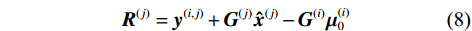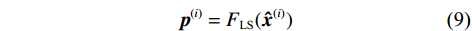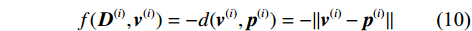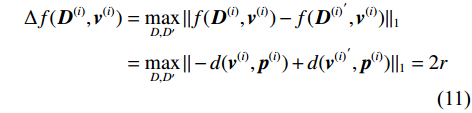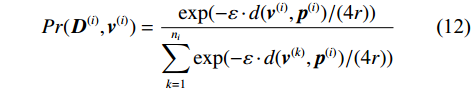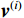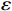Differential privacy-based cooperative positioning for satellite internet
-
摘要: 卫星互联网基于GNSS为用户提供定位、导航和定时服务,但GNSS协同定位过程会泄露包含用户位置信息的数据从而对用户隐私安全造成威胁. 针对当前GNSS协同定位隐私保护方面存在的问题,本文提出了一种基于差分隐私的卫星导航系统协同定位方法. 该方法首先生成扰动位置,并在满足隐私预算的前提下随机选择扰动位置计算定位协同数据,防止用户位置信息在协作过程中泄露. 实验结果表明:所提出的方法可以在保障定位准确率和实时性的前提下有效保护用户位置隐私,可为卫星互联网协同定位信息安全研究提供理论参考.Abstract: Satellite internet provides positioning, navigation and timing services for the whole world based on the Global Navigation Satellite System (GNSS), but the data containing users’ location information will be leaked during GNSS cooperative positioning process, which poses a threat to users’ privacy security. To address the current privacy-protection challenges in GNSS cooperative positioning systems, this paper proposes a differential privacy-based cooperative positioning method for GNSS systems. The method first generates the perturbed position and randomly selects one to calculate the positioning collaboration data under the premise of satisfying the privacy budget, so as to prevent the user’s location from being leaked during the collaboration process. The experimental results show that the proposed method can effectively protect user location privacy while guaranteeing real-time and accurate positioning service, which provides a theoretical reference for the research of GNSS cooperative positioning information security.
-
0. 引 言
卫星互联网通过多个互联互通的卫星系统为用户提供通信、定位、遥感等服务,在低轨巨型卫星互联网星座陆续开展建设、卫星导航相关技术持续提升的背景下,GNSS逐渐成为卫星互联网向用户提供时空信息的重要空间基础设施[1]. 尽管当前GNSS已为用户提供较高的定位准确率和较好的实时性,但卫星信号接收机仍易受到自然或人为干扰导致定位偏差. 随着对全球卫星导航定位技术的深入研究,一些民用专业领域(如智慧城市、电网监控等)对卫星导航抗干扰能力和定位精度提出了更高要求,GNSS协同定位技术因此受到日益广泛的关注. 协同定位是指通过将距离估计数据在多个邻近协作卫星信号接收机(如用户手机、车辆等)之间共享,联合多设备观测信息最小化各自或其中部分协作设备的定位信号干扰并提升定位准确率[2]. 相比单点定位的GNSS,协同GNSS定位更有利于消除观测误差提升卫星定位系统的整体精度.
尽管GNSS协同定位可以提升多卫星互联网用户定位准确率,但是隐含用户位置的距离估计信息在共享过程中泄露可能会对用户隐私安全造成威胁. 为了提升GNSS协同定位系统的可靠性,需要设计合适的用户位置隐私保护机制. 近年来,针对位置信息的隐私保护方案得到了广泛的研究. 文献[3]针对移动社交网络中用户位置隐私安全和效率问题,提出一种基于k-匿名批认证的用户位置隐私保护方案. 该方案先后通过假位置生成,位置熵筛选和真实用户位置合并来形成k-匿名以保障用户位置隐私. 为了保障车联网导航系统交换实时交通位置信息过程的安全性,文献[4]提出了一种基于椭圆曲线同态加密算法的轻量级签名聚合模型来实现高效的用户位置隐私保护,但是该方案难以适应高速车联网场景. 为了在保障车联网用户位置隐私的基础上进一步保护查询隐私,文献[5]提出了一种基于虚拟序列的位置隐私和查询隐私联合保护机制,通过将联合保护转化为虚拟序列的选择问题并建立保护优化模型来防止攻击者获得真实查询. 然而,当前关于位置隐私保护的工作主要针对移动社交网络和车联网进行设计,无法直接应用到卫星互联网和GNSS协同定位的场景中.
然而当前卫星互联网GNSS协同定位工作主要聚焦于提升定位准确率,忽视了协作过程隐私保护. 文献[6]研究了以Android智能手机作为卫星信号接收机场景下的GNSS协同定位准确度,该工作提出了一种基于网络移动用户距离估计的协同定位方法,并在真实的GNSS定位数据集上验证了方案在定位精度提升方面的有效性. 文献[7]提出了一种基于三维映射和因子图优化(factor graph optimization,FGO)的GNSS协同定位方法,缓解了卫星导航定位中多径和非可视径效应带来的随机误差并消除了大气延迟和卫星轨道偏差带来的系统误差. 在GNSS辅助的基础上,文献[8]进一步提出车载雷达测距与GNSS信息融合的协同定位方法,采用极大似然估计(maximum likelihood estimate,MLE)将定位问题构建为非线性优化模型,并通过半正定松弛和特征值分解求近似解,实现高精度实时定位. 总体来说,当前GNSS协同定位缺乏对设备共享定位数据的隐私保护,导致用户位置信息易被网络攻击者窃取,威胁用户隐私安全.
为了在确保卫星互联网协同定位准确率的前提下增强系统对于用户位置数据的隐私保护,本文提出基于差分隐私的GNSS协同定位方案. 差分隐私是一种保障用户数据可用性的同时提供数据隐私保护的有效方案[9],与传统的隐私保护方法(如加密算法)相比,差分隐私不仅能够提供较好的安全性,而且同时具有更低的计算复杂度,这契合卫星互联网对于协同定位实时性的需求. 结合差分隐私,本文首先对GNSS协同系统的定位估计模型进行描述,然后说明如何将差分隐私与协同定位过程有机结合,最后通过实验验证所提出方案的有效性,为卫星互联网协同定位信息安全研究提供理论参考.
1. GNSS协同定位系统
本文采用差分全球导航卫星系统 (Differential Global Navigation Satellite System,DGNSS)作为协同定位的基准模型[10],首先介绍DGNSS的定位原理,然后对基于加权最小二乘(weighted least squares,WLS)的协同定位估计算法进行介绍.
1.1 DGNSS协同定位模型
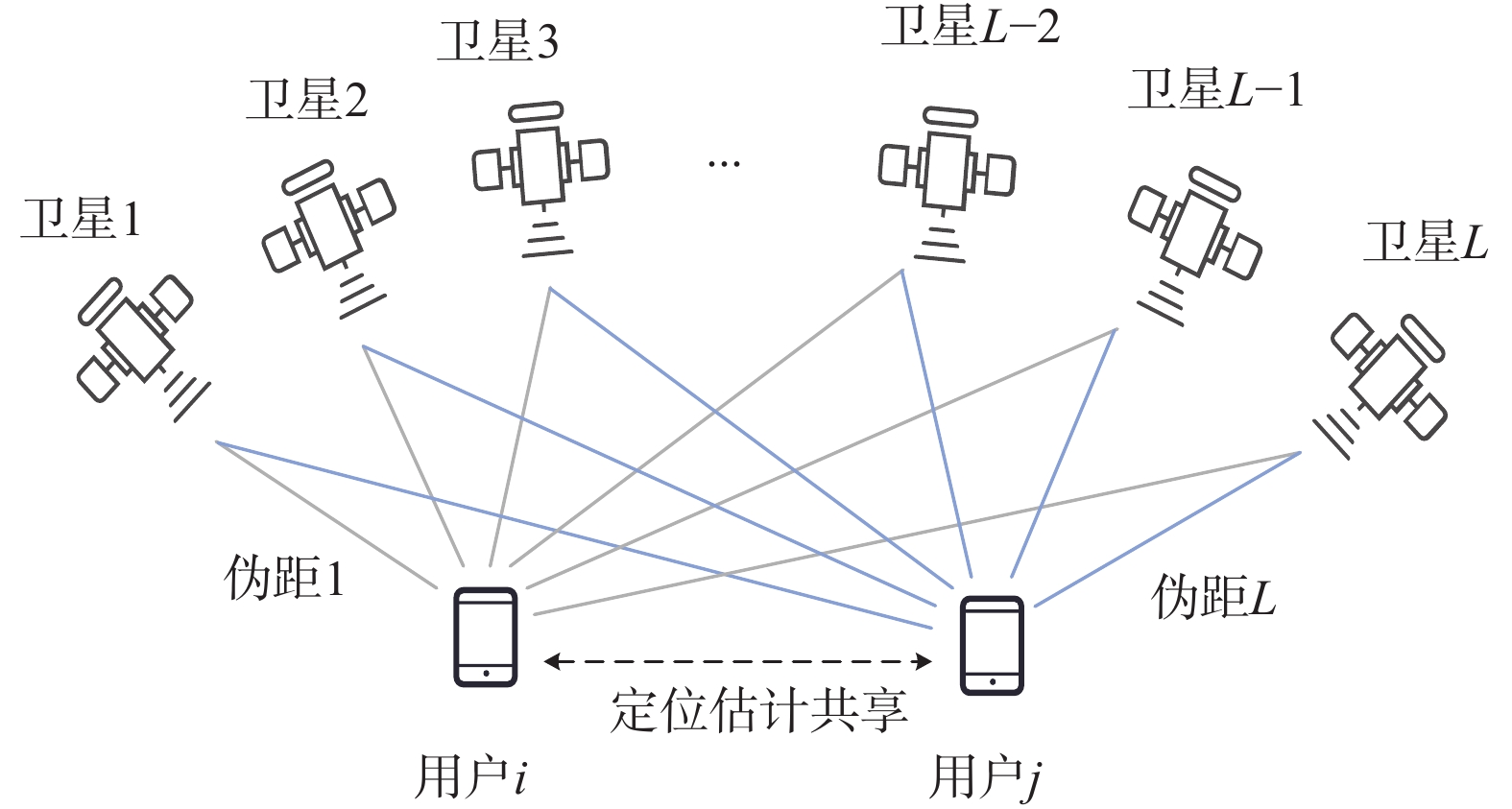
基于DGNSS的协同定位模型如图1所示,每一个GNSS接收机需要根据接收到的信号计算
$ L $ 个可视卫星的伪距和载波相位. 假设考虑的场景中有两个邻近的GNSS接收机,分别标记为$ i $ 和$ j $ ,这两个GNSS接收机可以从相同的卫星集合中接收到各自的导航信号并计算伪距观测变量. 该场景下第$ i $ 个接收机接收到来自第$ k $ 个卫星的伪距观测变量计算方式为$$ \rho _k^{(i)} = ||{{\boldsymbol{p}}^{(i)}} - {{\boldsymbol{p}}_k}|| + c(\delta {t^{(i)}} - \delta {t_k}) + {T_k} + {I_k} + \lambda _k^{(i)} $$ (1) 式中:
$ {{\boldsymbol{p}}^{(i)}} $ 为第$ i $ 个接收机的位置向量;$ {{\boldsymbol{p}}_{{k}}} $ 为第$ k(0 < k < L + 1) $ 个卫星的位置;$ \delta {t^{(i)}} $ 和$ \delta {t_k} $ 分别为未知的接收机时钟偏移和已知的卫星时钟偏移;$ c $ 为真空中的光速;$ {T_k} $ 和$ {I_k} $ 分别代表由对流层和电离层引起的时延误差;$ \lambda _k^{(i)}\sim {\mathrm{N}}(0,\sigma _{i,k}^2) $ 是用于表示包括伪距估计误差和其他未表示系统误差的随机变量,遵循正态分布. 基于此,第$ i $ 个接收机来自全部$ L $ 个卫星的伪距观测向量表示为$ {{\boldsymbol{\rho }}^{(i)}} = {\left[ {\rho _1^{(i)}, \cdots ,\rho _L^{(i)}} \right]^{\text{T}}} $ . 通过计算两个协作GNSS接收机的伪距差分可以消除对流层和电离层造成的大气时延,表示为$$ \begin{split} \Delta \rho _k^{(i,j)} =& \rho _k^{(i)} - \rho _k^{(j)} = ||{{\boldsymbol{p}}^{(i)}} - {{\boldsymbol{p}}_k}|| - ||{{\boldsymbol{p}}^{(j)}} - {{\boldsymbol{p}}_k}|| \\ &+ c(\delta {t^{(i)}} - \delta {t^{(j)}}) + \lambda _k^{(i,j)} \end{split} $$ (2) 其中,
$ \lambda _k^{(i,j)}\sim {\mathrm{N}}(0,\sigma _{i,k}^2 + \sigma _{j,k}^2) $ 为伪距差分过程中被放大的噪声. 类似地,L个卫星的伪距差分向量表示为$ {{\Delta }}{{\boldsymbol{\rho }}^{(i,j)}} = {\left[ {\Delta \rho _1^{(i,j)}, \cdots ,\Delta \rho _L^{(i,j)}} \right]^{\text{T}}} $ . 为了方便数学表示,使用$ {\boldsymbol{\lambda }} = {\left[ {\lambda _1^{(i,j)}, \cdots ,\lambda _L^{(i,j)}} \right]^{\text{T}}} $ 表示误差向量,使用非线性函数$ g({{\boldsymbol{x}}^{(i)}},{{\boldsymbol{x}}^{(j)}}):{\mathbb{R}^4} \times {\mathbb{R}^4} \mapsto {\mathbb{R}^L} $ 表示伪距差分向量中除误差之外的部分,从而伪距差分向量可重新表示为$$ \Delta {{\boldsymbol{\rho }}^{(i,j)}} = g({{\boldsymbol{x}}^{(i)}},{{\boldsymbol{x}}^{(j)}}) + {\boldsymbol{\lambda }} $$ (3) 1.2 基于WLS的定位估计方法
为了利用多个协同接收机的伪距差分向量对位置信息进行增强估计,首先使用
$ G = {\nabla _x}g( \cdot ) $ 表示$ g( \cdot ) $ 关于$ x $ 的全导,数并将函数$ g({{\boldsymbol{x}}^{(i)}},{{\boldsymbol{x}}^{(j)}}) $ 关于任意点$ {\boldsymbol{\mu }}_0^{(i)} $ 和$ {\boldsymbol{\mu }}_0^{(j)} $ 进行一阶泰勒级数线性展开,可得$$ g({{\boldsymbol{x}}^{(i)}},{{\boldsymbol{x}}^{(j)}}) \approx g({\boldsymbol{\mu }}_0^{(i)},{\boldsymbol{\mu }}_0^{(j)}) + G({\boldsymbol{x}} - {{\boldsymbol{\mu }}_{0}}) $$ (4) 式中:
$ {\boldsymbol{x}} $ 包含$ {{\boldsymbol{x}}^{(i)}} $ 和$ {{\boldsymbol{x}}^{(j)}} $ ;$ {\boldsymbol{G}} = \left[ {{{\boldsymbol{G}}^{(i)}}, - {{\boldsymbol{G}}^{(j)}}} \right] $ ,且$ {{\boldsymbol{G}}^{(i)}} $ 表示为$$ {{\boldsymbol{G}}}^{({i})}=\left[\begin{array}{cc}-{{\boldsymbol{u}}}_{1}^{\text{T}}({{\boldsymbol{x}}}^{(i)})& 1\\ \vdots &\vdots\\ -{{\boldsymbol{u}}}_{L}^{\text{T}}({{\boldsymbol{x}}}^{(i)})& 1\end{array}\right] $$ (5) 基于上述线性化操作,对
$ {{\boldsymbol{x}}^{(i)}} $ 和$ {{\boldsymbol{x}}^{(j)}} $ 的协同估计问题可以通过WLS算法迭代求解,首先依据式(4)构造线性方程$$ \begin{split} {{\boldsymbol{y}}^{(i,j)}} &= {{\boldsymbol{G}}^{(i)}}{{\boldsymbol{x}}^{(i)}} - {{\boldsymbol{G}}^{(j)}}{{\boldsymbol{x}}^{(j)}} + {\boldsymbol{\beta }} \\ &= {{\boldsymbol{G}}^{(i)}}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{P}}^{(i)}}} \\ {c\delta {t^{(i)}}} \end{array}} \right] - {{\boldsymbol{G}}^{(j)}}\left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{P}}^{(j)}}} \\ {c\delta {t^{(j)}}} \end{array}} \right] + {\boldsymbol{\beta }} \end{split} $$ (6) 式中,
$ {{\boldsymbol{P}}^{(i)}} = {\left[ {||{{\boldsymbol{p}}^{(i)}} - {{\boldsymbol{p}}_1}||, \cdots ,||{{\boldsymbol{p}}^{(i)}} - {{\boldsymbol{p}}_L}||} \right]^{\text{T}}} $ . 接着,在假定第$ i $ 个接收机可以收到第$ j $ 个接收机的距离估计值$ {{\boldsymbol{\hat x}}^{(j)}} $ 的前提下,对$ {{\boldsymbol{x}}^{(i)}} $ 进行估计$$ {{\boldsymbol{\hat x}}^{(i)}} = {\boldsymbol{\mu }}_0^{(i)}{({{\boldsymbol{G}}^{{{(i)}^{\text{T}}}}}{{\boldsymbol{D}}^{ - 1}}{{\boldsymbol{G}}^{(i)}})^{ - 1}}{{\boldsymbol{G}}^{{{(i)}^{\text{T}}}}}{{\boldsymbol{D}}^{ - 1}} \cdot {{\boldsymbol{R}}^{(j)}} $$ (7) 式中,
$ {{\boldsymbol{D}}^{(i)}} $ 为对角矩阵$ {\mathrm{diag}}(\sigma _{i,1}^2, \cdots, \sigma _{i,L}^2) $ ,$ {{\boldsymbol{R}}^{(j)}} $ 需依据接收机$ j $ 发送距离估计数据的通过下式计算:$$ {{\boldsymbol{R}}^{(j)}} = {{\boldsymbol{y}}^{(i,j)}} + {{\boldsymbol{G}}^{(j)}}{{\boldsymbol{\hat x}}^{(j)}} - {{\boldsymbol{G}}^{(i)}}{\boldsymbol{\mu }}_0^{(i)} $$ (8) 类似地,接收机
$ j $ 在收到$ {{\boldsymbol{\hat x}}^{(i)}} $ 后可更新估计值$ {{\boldsymbol{\hat x}}^{(j)}} $ . 由此可见,采用WLS算法进行协同定位要求协作接收机共享本地包含接收机与卫星之间距离估计信息的敏感数据,攻击者可通过单点定位估计破解用户位置,造成隐私安全威胁.2. 基于差分隐私的定位隐私保护机制
为了防止协同定位造成的数据泄露对用户隐私安全造成威胁,在DGNSS的基础上进一步引入
$ \varepsilon $ -差分隐私保护机制. 本节首先分析DGNSS中存在的威胁模型,然后介绍所提出的基于$ \varepsilon $ -差分隐私的协同定位算法.2.1 威胁模型
本文假定GNSS协同定位系统是不可信的,将GNSS接收机传递的定位估计信息视为敏感数据,并认为攻击者有兴趣暗中推理出接收机的位置,但是仍然保证系统正常运转. 在该系统中,攻击者可能来自系统外部或内部恶意节点,其通过被动方式采集系统广播信息但是不妨碍信息的传递.
对于第
$ i $ 个接收机,其广播的距离估计信息$ {{\boldsymbol{\hat x}}^{(i)}} $ 包括接收机$ i $ 和$ L $ 个卫星之间的距离,以及接收机的时钟偏移. 攻击者获得该信息后可简单地通过最小二乘法(least squares,LS)求解单点定位方程获得接收机坐标位置和时钟偏移(需满足$ L > 4 $ ),表示为$$ {{\boldsymbol{p}}^{(i)}} = {F_{{\text{LS}}}}({{\boldsymbol{\hat x}}^{(i)}}) $$ (9) 式中,
$ {F_{{\text{LS}}}}( \cdot ) $ 表示最小二乘映射函数. 为了避免接收机位置信息泄露,距离估计信息$ {{\boldsymbol{\hat x}}^{(i)}} $ 应当在发送前被混淆以使攻击者难以获得用户真实位置信息.2.2 基于
$ \varepsilon $ -差分隐私的协同定位算法对于第
$ i $ 个接收机,其真实位置$ {{\boldsymbol{p}}^{(i)}} $ 可以在广播至协作节点前通过式(9)进行单点估计. 接着定义关于接收机$ i $ 的位置集合$ {{\boldsymbol{D}}^{(i)}} $ ,其中的元素$ {{\boldsymbol{v}}^{(i)}} \in {{\boldsymbol{D}}^{(i)}} $ 满足$ ||{{\boldsymbol{v}}^{(i)}} - {{\boldsymbol{p}}^{(i)}}|| \leqslant r $ ,敏感因子$ r $ 表示定位扰动程度,扰动越大则隐私保护效果越好. 接收机$ i $ 附近的区域首先被划分为若干离散网格,并以网格的中心点作为干扰位置$ {{\boldsymbol{v}}^{(i)}} $ 的候选值. 接收机$ i $ 的评价函数被定义为$$ f({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) = - d({{\boldsymbol{v}}^{(i)}},{{\boldsymbol{p}}^{(i)}}) = - ||{{\boldsymbol{v}}^{(i)}} - {{\boldsymbol{p}}^{(i)}}|| $$ (10) 该评价函数的敏感度表示为
$$ \begin{split} \Delta f({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) &= \mathop {{\mathrm{max}}}\limits_{D,{D{'}}} ||f({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) - f({{\boldsymbol{D}}^{(i)}}^{'},{{\boldsymbol{v}}^{(i)}})|{|_1} \\ &= \mathop {{\mathrm{max}}}\limits_{D,{D{'}}} || - d({{\boldsymbol{v}}^{(i)}},{{\boldsymbol{p}}^{(i)}}) + d({{\boldsymbol{v}}^{(i)}}^{'},{{\boldsymbol{p}}^{(i)}})|{|_1} = 2r \end{split} $$ (11) 式中,
$ {{\boldsymbol{D}}^{(i)}} $ 和$ {{\boldsymbol{D}}^{(i)}}^{'} $ 是仅相差一条记录的邻接集合. 协作接收机在传递协同定位信息的过程,并不直接传递原始估计信息$ {{\boldsymbol{p}}^{(i)}} $ ,而是传递经差分隐私保护后的干扰位置$ {{\boldsymbol{v}}^{(i)}} $ . 根据差分隐私保护原理,为了保障接收机$ i $ 广播包含其真实位置$ {{\boldsymbol{p}}^{(i)}} $ 的$ \varepsilon $ -差分隐私,对于其给定的隐私预算$ \varepsilon $ ,选择$ \forall {{\boldsymbol{v}}^{(i)}} \in {{\boldsymbol{D}}^{(i)}} $ 作为干扰位置的概率为$$ Pr({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) = \frac{{\exp ( - \varepsilon \cdot d({{\boldsymbol{v}}^{(i)}},{{\boldsymbol{p}}^{(i)}})/(4r))}}{{\displaystyle\sum_{k = 1}^{{n_i}} {\exp ( - \varepsilon \cdot d({{\boldsymbol{v}}^{(k)}},{{\boldsymbol{p}}^{(i)}})/(4r))} }} $$ (12) 式中,
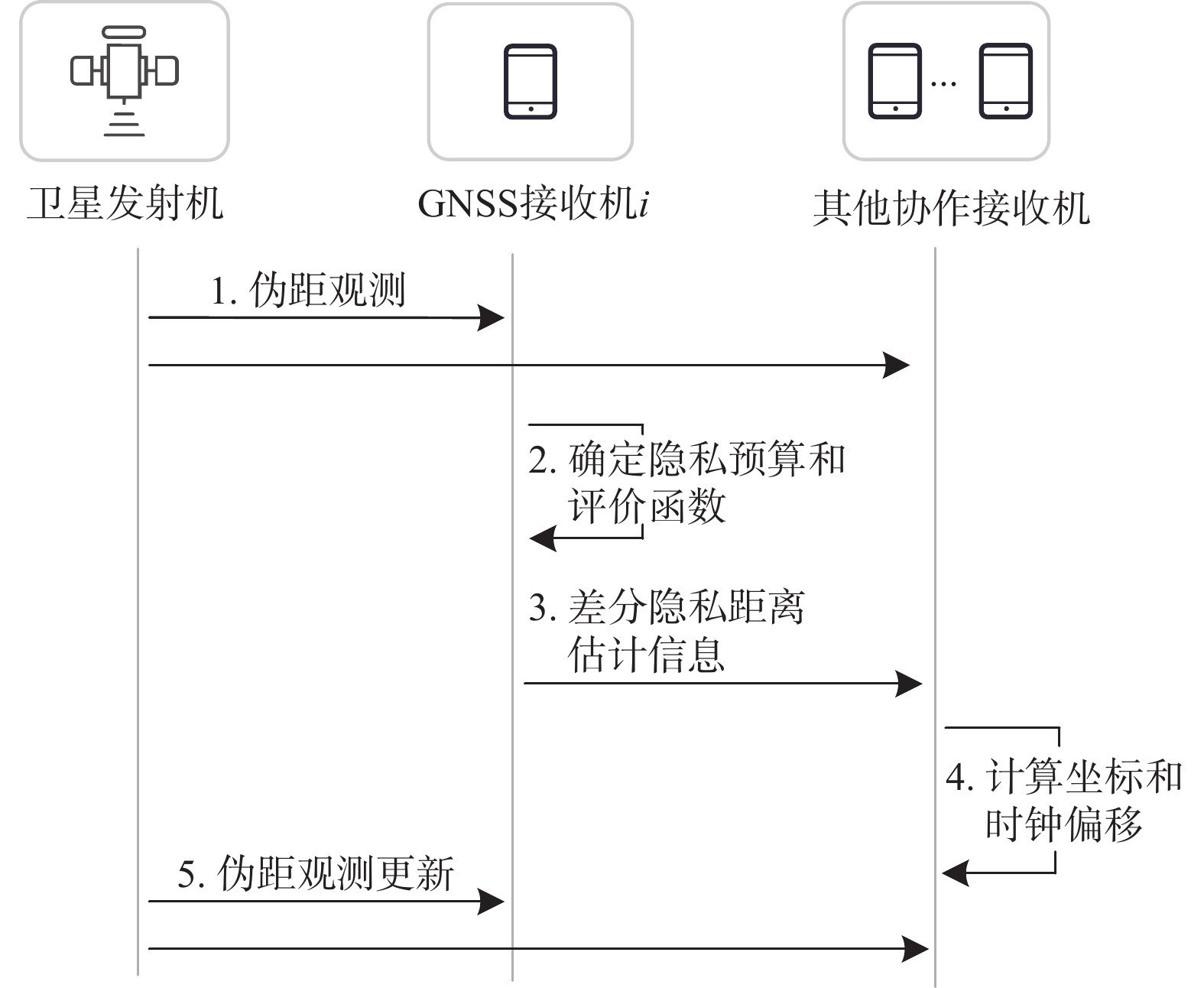
$ {n_i} $ 表示集合$ {{\boldsymbol{D}}^{(i)}} $ 的大小. 当接收机$ i $ 按照式(12)选择干扰位置$ {{\boldsymbol{v}}^{(i)}} $ 之后,代替$ {{\boldsymbol{p}}^{(i)}} $ 重新计算和$ L $ 个卫星之间的距离并得到混淆后的广播信息$ {{\boldsymbol{\tilde x}}^{(i)}} = \left\{ {{{{\boldsymbol{\tilde P}}}^{(i)}},c\delta {t^{(i)}}} \right\} $ . 隐私预算表征了接收机对差分隐私保护程度的需求,隐私预算越小则隐私保护效果越好. 基于$ \varepsilon $ -差分隐私的协同定位算法流程如图2所示,可以概括为四个阶段:1) 阶段1:所有协作GNSS接收机获得相对
$ L $ 个卫星的伪距观测,确定其隐私预算$ \varepsilon $ ,以及相关隐私参数$ r $ . 根据参数进一步确定具体的评价函数$ f({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) $ 和敏感度$ \Delta f({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) $ .2) 阶段2:确定概率
$ Pr({{\boldsymbol{D}}^{(i)}},{{\boldsymbol{v}}^{(i)}}) $ 并为所有协作接收机选取扰动位置$ {{\boldsymbol{v}}^{(i)}} \in {{\boldsymbol{D}}^{(i)}} $ . 依据所选取的扰动位置,进一步计算隐私保护后的距离估计信息$ {{\boldsymbol{\tilde x}}^{(i)}} $ .3) 阶段3:协作GNSS接收机接收到其他节点发送的距离估计信息
$ {{\boldsymbol{\tilde x}}^{(i)}} $ ,联合本地距离估计信息WLS算法更新估计值$ {{\boldsymbol{\tilde x}}^{(j)}} $ .4) 阶段4:协作GNSS接收机根据
$ {{\boldsymbol{\tilde x}}^{(j)}} $ 通过LS算法求解其定位坐标$ {{\boldsymbol{p}}^{(j)}} $ 及时钟偏移.3. 实验结果与分析
本节将所提出的基于
$ \varepsilon $ -差分隐私的协同定位方案和其他隐私保护方案进行比较,在不同隐私参数设置下测试其对时间开销和系统定位误差的影响. 本节首先介绍实验环境和参数设置,然后对实验结果进行展示和分析.3.1 实验设置
本实验在一台拥有16 GB内存,NVIDIA GeForce RTX 2060显卡,AMD Ryzen 4800H 8核心处理器的计算机上基于MATLAB R2023b软件模拟GNSS协同定位系统,该系统由6台全球定位卫星和直线距离约450 m的2台GNSS接收机组成,其绝对经纬度坐标分别为(31°01'47.2"N, 121°26'26.4"E)和(31°01'33.0"N, 121°26'30.2"E). 实验涉及的关键仿真参数设置如表1所示.
表 1 关键仿真参数设置参数 数值 参数 数值 卫星数 (L) 6 伪距误差方差 ($ \sigma _{i,k}^2 $) 10 敏感因子 ($ r $) 10 隐私预算 ($ \varepsilon $) 10 作为对比,除了所提出的基于差分隐私的协同定位方法,本文还比较了其他两种方案,分别是不采取隐私保护的方案和基于RSA加密[11]的隐私保护方案. 其中基于RSA加密的方案要求协作接收机双方首先共享公钥,在发送距离估计信息时需首先使用对方的公钥进行加密. RSA算法关键参数可以表示为三元组
$ (n,e,d) $ ,其中$ n = p \times q $ 是两个质数的乘积,$ p $ 与$ q $ 分别从前150个质数中随机选取,且满足$ e $ 与$ Q = (p - 1) \times (q - 1) $ 互质,$ d \times e = 1\text{mod} Q $ .3.2 时间开销测试
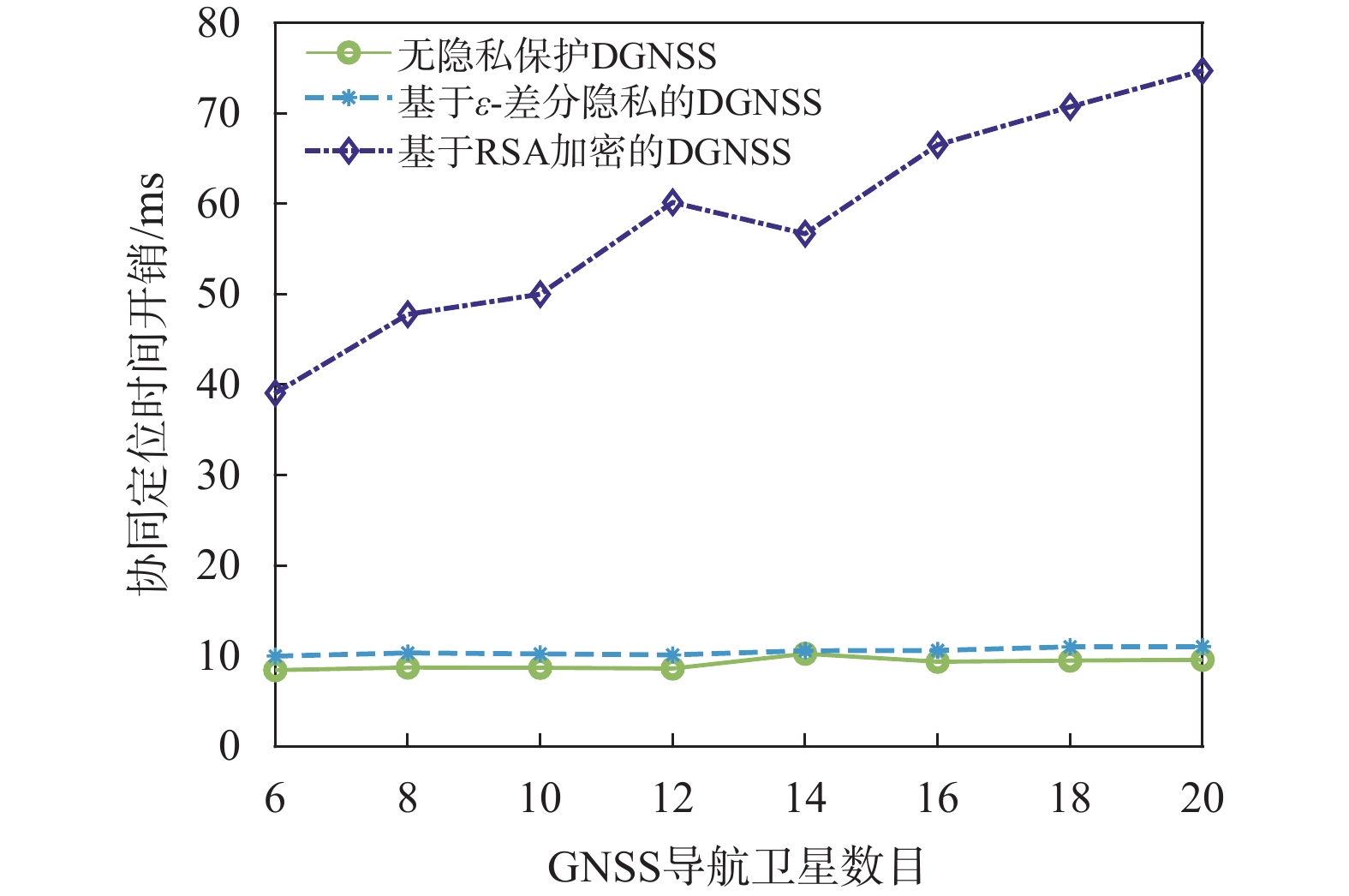
由于GNSS定位的实时性是衡量系统性能的重要指标,因此首先对三种方案的时间开销进行测试. 其中,所提出的基于差分隐私协同定位方案的时间开销包括本地差分隐私计算时延和定位估计传播时延. 基于RSA加密的方案包括密钥传输时延,加解密处理时延,以及数据传播时延. 不采取隐私保护的协同定位方案则仅需计算距离估计数据传播时延. 在此过程种假定协同接收机之间的传输带宽和信道状态是不变的. 图3显示了三种方案的时间开销和系统中导航卫星数目的关系. 随着卫星数目的增加,接收机获得的距离估计信息增加,从而使得定位估计参数
$ {{\boldsymbol{p}}^{(i)}} $ 和差分隐私干扰位置$ {{\boldsymbol{v}}^{(i)}} $ 的维度均增加,导致更高的时间开销. 其中没有隐私保护的方案时间开销且增长速度最慢,因为其仅对传输数据量的增长敏感. 由于额外的干扰位置选择和隐私保护信息生成过程,基于差分隐私的方案时间开销略高于(10%以内)无隐私保护方案. 基于RSA加密方案的时间开销及其增长速度远高于其他两种方案,因为增加的数据维度将直接提升加解密的复杂度并显著增加数据处理时延. 实验结果表明,所提出的基于差分隐私的DGNSS方案可以在有效地保护定位隐私的取得可忽略的时间开销成本,保障GNSS定位实时性.3.3 定位误差测试
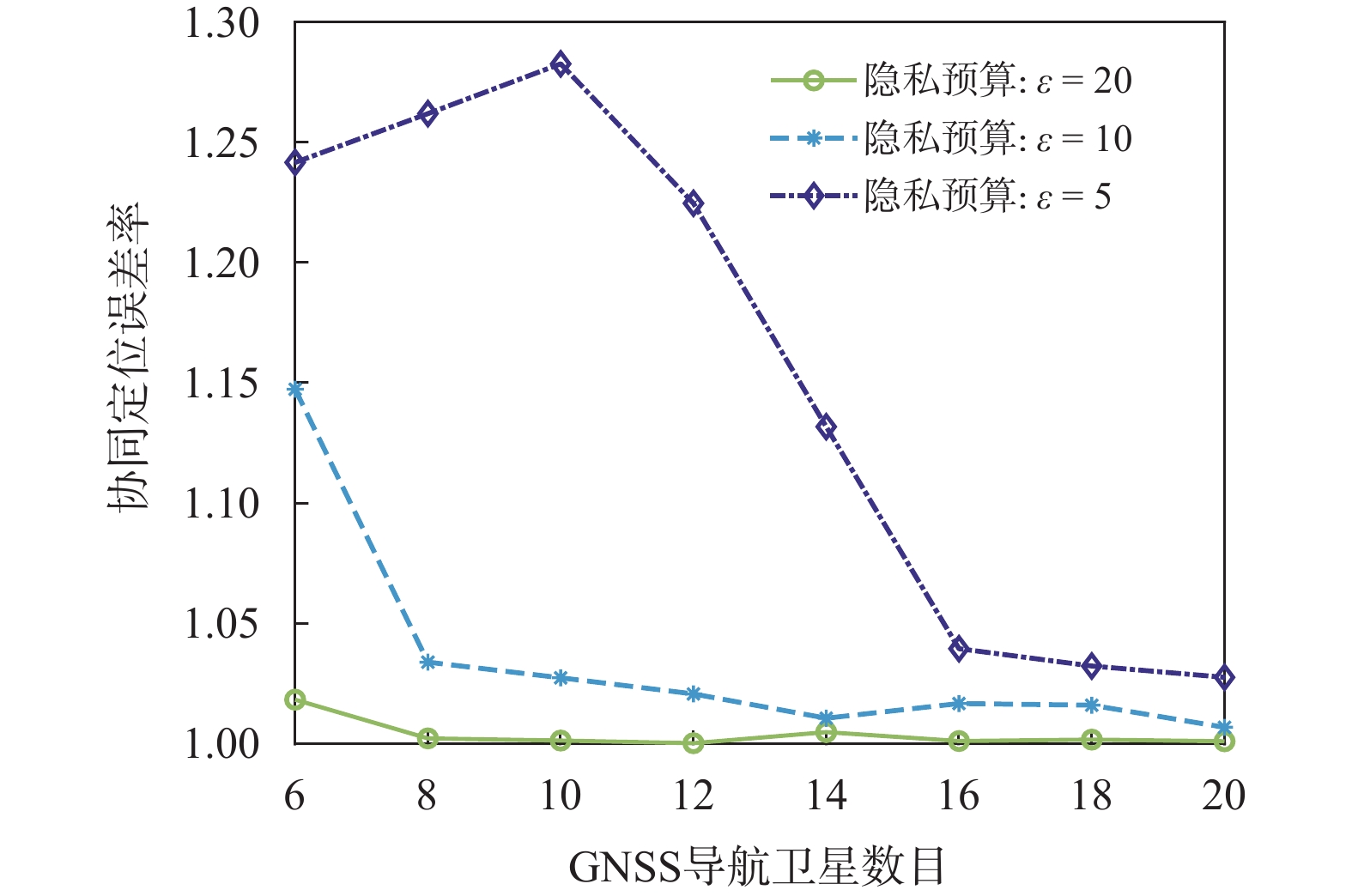
引入差分隐私保护机制后,系统中将存在隐私保护程度和定位精度之间的权衡,本小节将探究这一权衡与系统中各变量之间的关系. 由于采用RSA加密的方案在加解密后不改变原始数据信息,因此其计算得到的定位误差和不采用任何隐私保护方案的定位误差相同,本小节将这两种方案计算得到的定位误差作为基准误差,并将采用差分隐私方案的定位误差与基准误差的比值称为定位误差率. 定位误差率表征了基于差分隐私的定位方案与基线方案准确率的接近程度,消除了导航卫星数目变化对基准误差值造成的波动,可以更直观地体现不同隐私预算方案对协同定位精度的影响. 图4显示了所提出方案的定位误差率随卫星数目和隐私预算之间的关系. 实验结果表明所提出的基于差分隐私的方案的定位精度同时受GNSS导航卫星数目以及隐私预算的影响. 一方面,当导航卫星数目增加时,所提出方案的定位精度将逐渐提高,体现在图中的定位误差率逼近1,即逼近基准误差. 另一方面,当隐私预算降低时,隐私保护程度增强,这将导致对系统定位估计产生较大噪声,因此定位误差率显著提高. 但是当GNSS系统导航卫星数目较多时(大于14),对低隐私预算带来的定位误差则有所补偿,体现为定位误差率减少至较低水平.
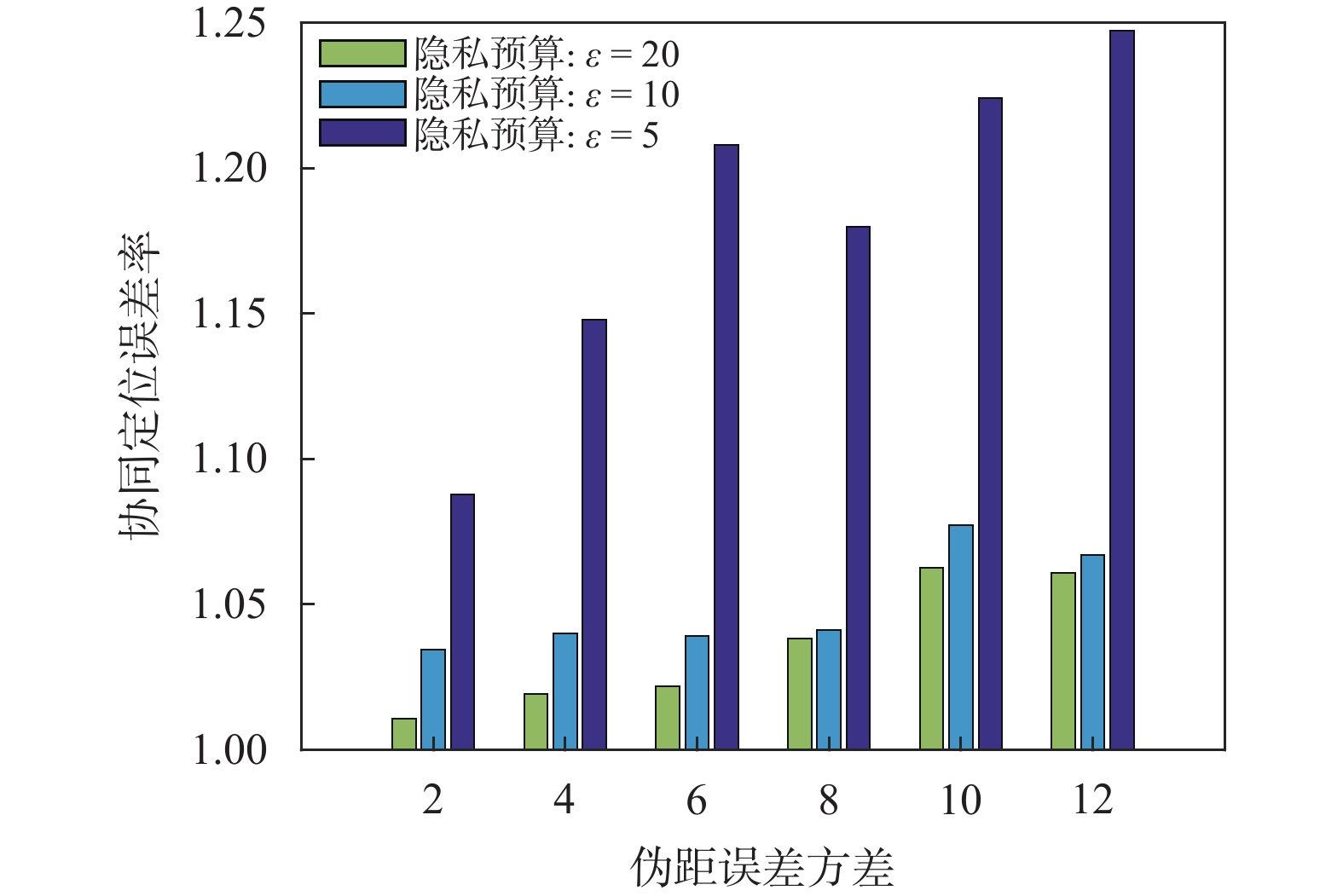
图5显示了所提出方案的定位误差率随伪距误差方差和隐私预算之间的关系. 当伪距误差方差较小时,协同定位误差率对隐私预算的改变更为敏感,体现为
$ \varepsilon = 5 $ 和$ \varepsilon = 10 $ 下的定位误差率相差较多. 当伪距误差方差增大时,伪距误差方差将成为参数估计误差的主要来源,此时系统在较小隐私预算($ \varepsilon \leqslant 10 $ )下的定位误差率相近,当隐私预算进一步增加至20,差分隐私引入的误差显著增加,协同定位误差率也明显提高. 总体来说,当合理控制差分隐私的隐私预算时,可以实现定位数据隐私保护的同时对系统协同定位精度造成可忽略的影响.4. 结束语
本文针对卫星互联网协同定位过程中存在的位置数据隐私安全问题,提出了基于差分隐私的隐私保护机制,可实现在几乎不影响导航系统定位精度和实时性的前提下保障用户位置信息安全. 实验结果表明,所提出的基于
$ \varepsilon $ -差分隐私的DGNSS方案相比基于RSA加密的方案具有更低的计算复杂度,且具有和不采用隐私保护的方案相近的时间开销. 此外,在合理控制隐私预算的前提下,可以实现高于基线定位误差10%以内的误差率,保障定位系统的可用性. 综上,本文将差分隐私机制引入协同卫星导航系统是可行和有效的,可为卫星互联网协同定位系统信息安全研究提供理论参考. -
表 1 关键仿真参数设置
参数 数值 参数 数值 卫星数 (L) 6 伪距误差方差 ($ \sigma _{i,k}^2 $) 10 敏感因子 ($ r $) 10 隐私预算 ($ \varepsilon $) 10 -
[1] 蔺陆洲, 邓平科. 低轨卫星导航系统建设与应用思考[J]. 卫星应用, 2023(2): 8-12. DOI: 10.3969/j.issn.1674-9030.2023.02.005 [2] HERNANDEZ G, LAMOUNTAIN G, CLOSAS P. Privacy-preserving cooperative GNSS positioning[J]. Journal of the institute of navigation, 2023, 70(4). DOI: 10.13140/RG.2.2.33970.02246
[3] 杨囡囡, 宋成. K-匿名批量认证的位置隐私保护机制[J]. 重庆邮电大学学报(自然科学版), 2023, 35(3): 468-473. [4] ZHAO Y N, HOU Y Z, WANG L L, et al. An efficient certificateless aggregate signature scheme for the internet of vehicles[J]. Transactions on emerging telecommunications technologies, 2020, 31(5): e3708. DOI: 10.1002/ett.3708
[5] 赵国锋, 吴昊, 王杉杉, 等. 车联网POI查询中的位置隐私和查询隐私联合保护机制[J]. 电子与信息学报, 2024, 46(1): 155-164. DOI: 10.11999/JEIT221599 [6] VERHEYDE T, BLAIS A, MACABIAU C, et al. SmartCoop algorithm: improving smartphones position accuracy and reliability through collaborative positioning[C]//International Conference on Localization and GNSS (ICL-GNSS), 2021.
[7] ZHANG G H, NG H-F, WEN W S, et al. 3D mapping database aided GNSS based collaborative positioning using factor graph optimization[J]. IEEE transactions on intelligent transportation systems, 2021, 22(10): 6175-6187. DOI: 10.1109/TITS.2020.2988531
[8] 屈小媚, 王世法, 谭屈山, 等. 基于测距与GNSS信息融合的车联网协同定位技术[J/OL]. (2024-01-18)[2024-02-01]. 计算机应用研究, 2024. [9] PAN Q Q, WU J, ZHENG X, et al. Differential privacy and IRS empowered intelligent energy harvesting for 6G internet of things[J]. IEEE internet of things journal, 2022, 9(22): 22109-22122. DOI: 10.1109/JIOT.2021.3104833
[10] 于晓东, 吕志伟, 王兵浩, 等. DGNSS数据传输格式RTCM3.2的介绍及解码研究[J]. 全球定位系统, 2015, 40(3): 37-41. [11] NI J B, ZHANG K, YU Y, et al. Identity-based provable data possession from RSA assumption for secure cloud storage[J]. IEEE transactions on dependable and secure computing, 2022, 19(3): 1753-1769. DOI: 10.1109/TDSC.2020.3036641



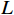

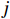




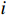











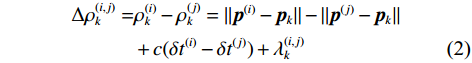




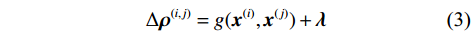
 下载:
下载: