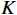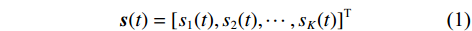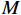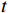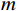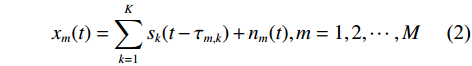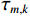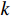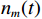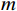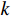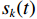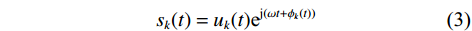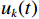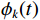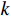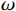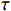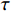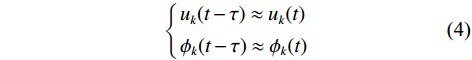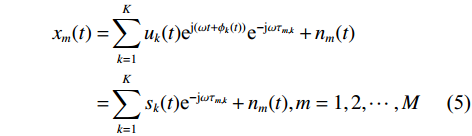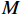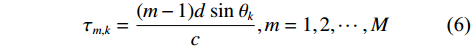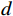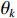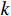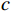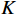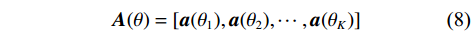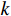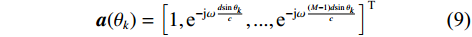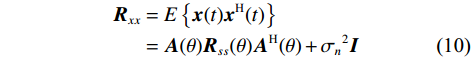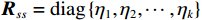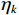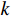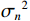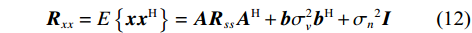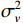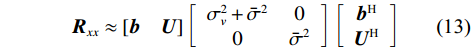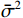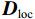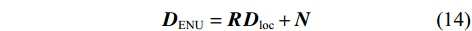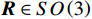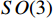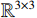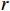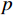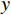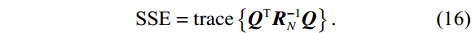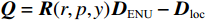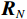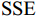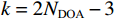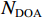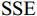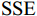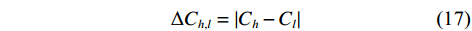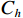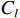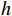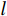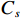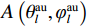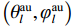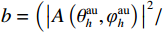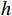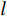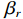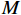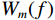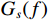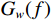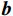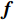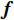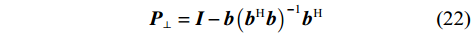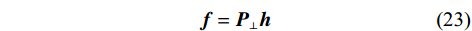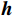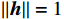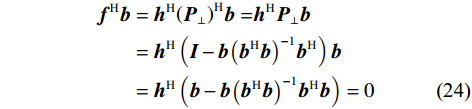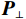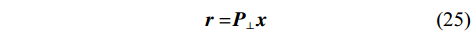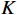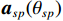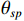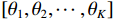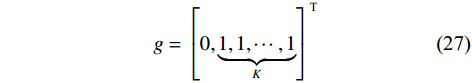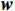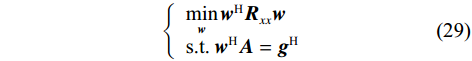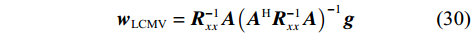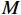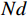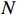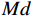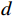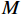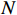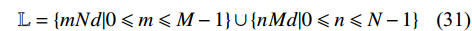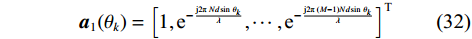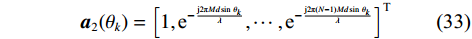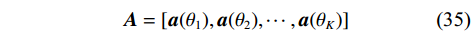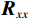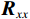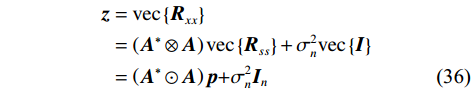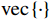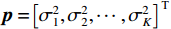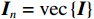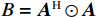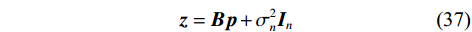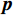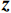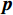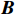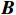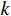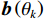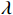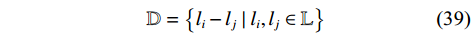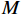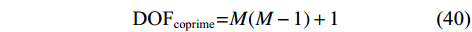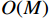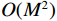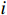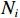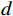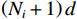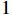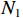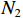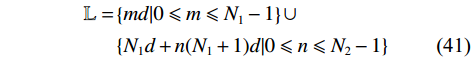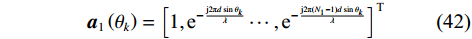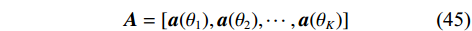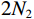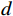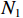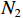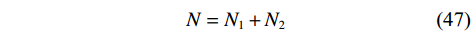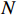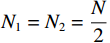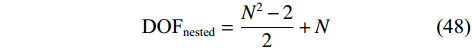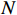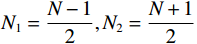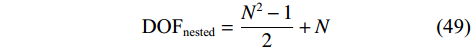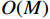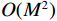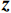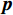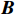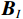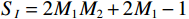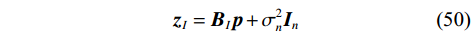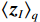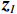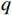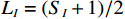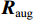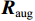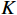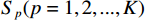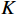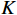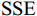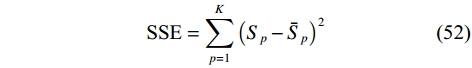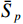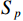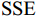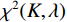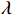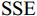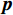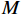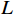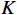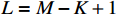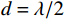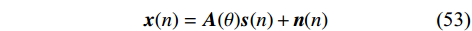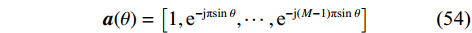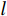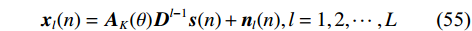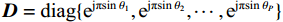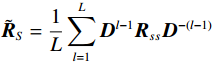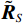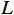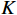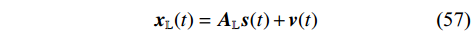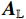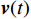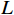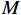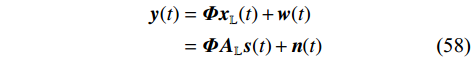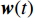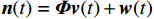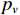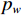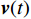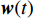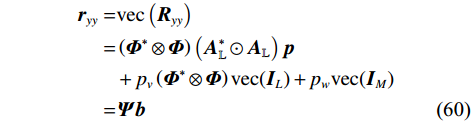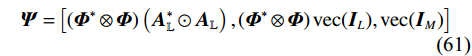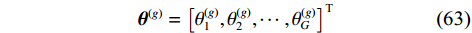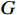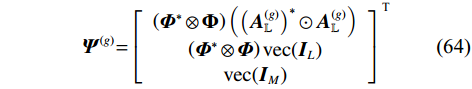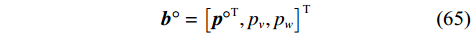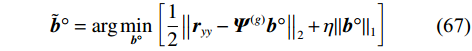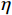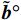Anti-spoofing technology based on array antenna signal processing
-
摘要: GNSS在国家基础设施以及生命安全应用中扮演重要角色,但日益增长的欺骗干扰事件给GNSS带来了巨大威胁. 本文介绍了基于阵列天线信号处理的防欺骗技术,根据阵列构型的不同,从均匀阵列和稀疏阵列两个方面总结了欺骗干扰检测与欺骗干扰抑制方法. 其中稀疏阵列相较均匀阵列,在相同天线阵元数的情况下,拥有更大的阵列孔径及自由度,极大地降低了设备成本,但其对相干信号处理技术要求更高. 最后本文给出了防欺骗干扰技术面临的难题以及其未来的发展趋势.Abstract: Global navigation satellite systems play an important role in national infrastructure as well as life safety applications, but the increasing spoofing incidents pose a great threat to GNSS. This paper introduces the anti-spoofing technology based on array antenna signal processing, and summarizes the spoofing interference detection and spoofing interference suppression methods from both uniform and sparse arrays according to the different array configurations. Compared with uniform array, sparse array has larger array aperture and degree of freedom under the same number of antenna elements, which greatly reduces the cost of equipment, but its coherent signal processing technology requires more. Finally, this paper gives the difficulties faced by the anti-spoofing interference technology and its future development trend.
-
Keywords:
- spoofing /
- sparse array /
- direction of arrival estimation /
- subspace projection /
- beamforming
-
0. 引 言
定位、导航与授时(positioning, navigation and timing,PNT)系统为各行业提供包括位置、速度和时间等关键时空基准信息服务[1],现代的PNT服务主要基于GNSS,在电力系统、通信系统和交通系统等国家基础设施及生命安全应用中发挥着重要的作用. 但是GNSS信号到达地面功率十分微弱,且民用信号结构公开,易受到人为的干扰.
人为干扰一般分为压制式干扰和欺骗式干扰. 其中,欺骗式干扰利用公开的GNSS信号结构来构造功率略大于真实信号的合法GNSS信号,企图给被欺骗者提供错误的时间和位置信息,甚至将目标诱骗到攻击者指定的位置. 欺骗式干扰由于具有隐蔽性,能在被攻击者毫不知情的情况下实现攻击,严重危害用户安全. 在冲突频繁的地区欺骗干扰现象日益增多. 2023年8月29日,巴西航空工业公司650机组人员在巴格达上空受到欺骗干扰攻击,飞机偏离轨道约有80 n mile,他们在没有获得许可的情况下几乎闯进伊朗领空[2]. 而在2023年10月7日哈马斯激进组织发动对以色列的突袭后,于地中海附近飞行的飞机在以色列多地上空短暂消失,原因可能是以色列为保护自己免受导弹威胁,在北部大部分空域对GPS信号进行扰乱[3]. 若飞机受到欺骗攻击并在毫不知情的情况下进入到未经授权的空域,很有可能会被截停甚至击落,造成不可挽回的损失. 面对日益增长的欺骗干扰威胁,防欺骗技术成为弹性健壮、安全可信的综合PNT体系中重要的一环.
防欺骗技术根据介入的阶段不同分为信息层处理技术和信号层处理技术,如表1所示. 信息层处理技术主要基于接收机自主完好性监测(receiver autonomous integrity monitoring,RAIM)[4-5],通过对信号进行捕获解算,分析异常的数据特征进行对欺骗干扰的检测. 常见的观测量有纯伪距[6]、伪距残差[7]、多普勒-钟飘双差等[8-9],通过与冗余信息比对进行一致性检验,判断信号是否受到欺骗干扰攻击. 而在信息层进行欺骗干扰抑制主要依靠对信息的加密认证,利用导航电文中的预留位或者添加新的信息位和加密算法实现对信息安全性的保障[10-12]. 信号层处理技术使用单天线、阵列天线和辅助传感器等对信号进行接收,不仅通过分析信号异常的物理特征实现对欺骗干扰的检测,而且可调整天线在不同方向的增益等方法实现对欺骗干扰的抑制. 使用单天线接收信号进行观测,检测量有载噪比(carrier to noise ratio,CNR)[13-14]、载波相位[15]、相关峰[16-19]等,也有通过改变接收机环路实现矢量跟踪来判断是否存在欺骗干扰[20-22],通过最大似然估计(maximum likelihood estimation, MLE)[23]和自动增益控制(automatic gain control,AGC)[24]进行欺骗干扰抑制. 使用阵列天线进行信号处理是目前最有效的防欺骗手段,检测量主要有信号强度和波达方向(direction of arrival, DOA),通过功率倒置、波束形成、子空间投影、空时自适应处理等手段进行欺骗干扰抑制[25]. 使用辅助传感器可以得到更多的观测量,从而判断是否存在欺骗干扰,目前常使用的辅助传感器有惯性测量单元(inertial measurement unit, IMU)[26-27]、高度计[28]等.
表 1 GNSS防欺骗技术项目 信息层 信号层 单天线 阵列天线 辅助传感器 检测 伪距、
伪距残差、
多普勒-钟飘双差等CNR、
载波相位、
相关峰、
矢量接收机等信号强度、
DOA等IMU、
高度计等抑制 信号加密认证 MLE、AGC等 功率倒置、
波束形成、
子空间投影、
空时自适应处理等- 阵列天线是强大的空域信号处理工具,阵列天线信号处理利用的是不同阵元接收信号之间的相位信息,能获取信号的功率和DOA等物理特征,并且可以通过对每个天线阵元的相位和振幅进行精确控制,形成特定方向的波束. 由于欺骗干扰一般是单个欺骗源播发多颗卫星的虚假信号,经过相同的传输信道到达接收机,欺骗信号的物理特征之间具有很强的相关性,这是攻击者无法伪造的特征,而这些物理特征可以通过阵列天线获取,因此阵列天线在欺骗干扰的检测和抑制上具有很大优势. 传统阵列天线信号处理使用的是阵元间距相同的均匀阵列,阵元间距一般为半波长,天线孔径正比于天线阵元数. 阵元数越大,天线物理孔径越大,空间分辨率和空间自由度也越高,但与此同时成本也随之上升,这限制了阵列天线信号处理技术的规模化应用. 如何在不增加天线阵元数的情况下,增大天线孔径及空间自由度,成为一个研究问题. 其中,稀疏阵列通过不均匀的阵元间距,使不同阵元接收信号之间的相位差满足一定关系,从而将物理阵列虚拟化形成一个阵元数更多的均匀阵列,在使用更少的天线单元的情况下达到甚至超过均匀阵列的性能,减小了信号接收系统和处理系统的规模,降低了设备成本,具有很大的应用前景.
本文介绍了基于阵列天线信号处理的防欺骗技术,并针对均匀阵列防欺骗技术与稀疏阵列防欺骗技术展开讲述,介绍阵列天线检测、抑制欺骗信号的原理以及不同阵列构型对防欺骗性能带来的影响,最后分析了现有防欺骗技术的应用难点与未来防欺骗技术的发展趋势.
1. 均匀阵列防欺骗技术
阵列天线是由多个天线阵元组成的天线系统,这些阵元按照特定的几何结构排列在一起,根据不同阵元接收信号之间不同的相位差,实现对信号参数的估计. 通过对每个天线阵元的相位和振幅进行精确控制,阵列天线可以形成特定方向的波束,将天线方向图的主瓣指向所需的方向,将干扰置零. 阵列天线最基本的构型就是均匀阵列,本节将介绍阵列天线信号处理的基本原理以及相应的均匀阵列欺骗干扰检测和抑制技术.
1.1 窄带信号观测模型
假设有
$K$ 个远场窄带信号$$ \boldsymbol{s}(t) = {\left[ {{s_1}(t),{s_2}(t),\cdots,{s_K}(t)} \right]^{\text{T}}} $$ (1) 入射到
$M$ 个增益为1的各向同性阵元组成的均匀线阵,且阵元间无互耦和误差,阵元接收信号噪声为高斯白噪声,各阵元噪声相互统计独立. 则在$t$ 时刻第$m$ 个阵元的输出为$$ {x_m}(t) = \sum\limits_{k = 1}^K {{s_k}(t - {\tau _{m,k}})} + {n_m}(t),m = 1,2,\cdots,M $$ (2) 式中:
${\tau _{m,k}}$ 为第$k$ 个信号到达第一个阵元与到达第$m$ 个阵元的时间差;${n_m}(t)$ 为第$m$ 个阵元上的观测噪声.对于窄带信号源,第
$k$ 个入射信号${s_k}(t)$ 可以表示成复包络的形式$$ {s_k}(t) = {u_k}(t){{\text{e}}^{{\text{j}}(\omega t + {\phi _k}(t))}} $$ (3) 式中:
${u_k}(t)$ 和${\phi _k}(t)$ 分别为第$k$ 个信号的幅度和相位;$\omega $ 为信号中心频率;对于远场信号,当$\tau $ 很小时,信号包络和相位在$\tau $ 时间内的变化可以忽略,则$$ \left\{ \begin{gathered} {u_k}(t - \tau ) \approx {u_k}(t) \\ {\phi _k}(t - \tau ) \approx {\phi _k}(t) \\ \end{gathered} \right. $$ (4) 由(2)~(4)可得
$$ \begin{split} {x_m}(t) =& \sum\limits_{k = 1}^K {{u_k}(t){{\text{e}}^{{\text{j}}(\omega t + {\phi _k}(t))}}{{\text{e}}^{ - {\text{j}}\omega {\tau _{m,k}}}} + {n_m}(t)} \\ =& \sum\limits_{k = 1}^K {{s_k}(t){{\text{e}}^{ - {\text{j}}\omega {\tau _{m,k}}}} + {n_m}(t),m = 1,2,\cdots,M} \end{split} $$ (5) 对于
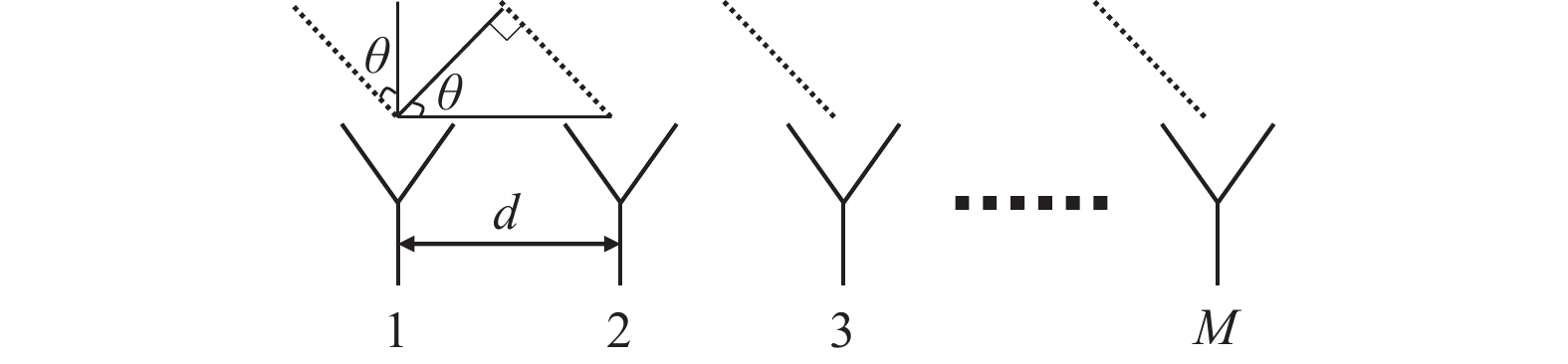
$M$ 元均匀线阵,其阵列示意图如图1所示,则$$ {\tau _{m,k}} = \frac{{(m - 1)d\;{\mathrm{sin}}\;{\theta _k}}}{c},m = 1,2,\cdots,M $$ (6) 式中:
$d$ 为阵元间距;${\theta _k}$ 为第$k$ 个信号的入射角;$c$ 为真空条件下的光速. 则阵列接收信号向量可以进一步写成$$ {\boldsymbol{x}}(t) = {{\boldsymbol{A}}}(\theta ){{\boldsymbol{s}}}(t) + {{\boldsymbol{n}}}(t) $$ (7) 式中,
$K$ 个入射信号的导向矩阵为$$ {{\boldsymbol{A}}}(\theta ) = \left[ {{{\boldsymbol{a}}}({\theta _1}),{{\boldsymbol{a}}}({\theta _2}),\cdots,{{\boldsymbol{a}}}({\theta _K})} \right] $$ (8) 第
$k$ 个信号的导向向量为$$ {{\boldsymbol{a}}}({\theta _k}) = {\left[ {1,{{\text{e}}^{ - {\text{j}}\omega \frac{{d\mathrm{sin}\;{\theta _k}}}{c}}},...,{{\text{e}}^{ - {\text{j}}\omega \frac{{(M - 1)d\mathrm{sin}\;{\theta _k}}}{c}}}} \right]^{\text{T}}} $$ (9) 假设阵元接收到信号之间和信号与观测噪声之间相互独立,阵列输出的自相关矩阵为
$$ \begin{split} {{{\boldsymbol{R}}}_{xx}} &= E\left\{ {{{\boldsymbol{x}}}(t){{{\boldsymbol{x}}}^{\text{H}}}(t)} \right\} \\ & = {{\boldsymbol{A}}}(\theta ){{{\boldsymbol{R}}}_{ss}}(\theta ){{{\boldsymbol{A}}}^{\text{H}}}(\theta ) + {\sigma _n}^2{{\boldsymbol{I}}} \end{split} $$ (10) 式中:
${{{\boldsymbol{R}}}_{ss}} = {\mathrm{diag}}\left\{ {{\eta _1},{\eta _2},\cdots,{\eta _k}} \right\}$ 为接收信号的自相关矩阵;${\eta _k}$ 为第$k $ 个信号的功率;${\sigma _n}^2$ 为噪声的功率;${{\boldsymbol{I}}}$ 为单位矩阵.1.2 欺骗干扰检测
在没有欺骗干扰的情况下,不同卫星的真实信号在空间中经过不同的传输信道到达接收机,而欺骗干扰一般是单个欺骗源播发多颗卫星的虚假信号,经过相同的传输信道到达接收机. 目前的欺骗干扰检测思路,利用的就是欺骗信号经过相同传输信道传播而带来的某些物理特征的强相关性以及由于强其相关性衍生出的其他异常特征,而阵列天线是获取这些特征的有力工具.
1.2.1 基于功率异常的欺骗干扰检测
在欺骗场景中,阵列天线的接收信号表示如下:
$$ {{\boldsymbol{x}} = {\boldsymbol{As}} + {\boldsymbol{bv}} + {\boldsymbol{n}}} $$ (11) 式中:
${{\boldsymbol{b}}}$ 为欺骗信号的导向矩阵;${{\boldsymbol{v}}}$ 为欺骗信号向量. 事实上,所有欺骗信号来自于同一方向,故它们具有相同的导向向量. 根据式(11)得到接收信号的协方差矩阵,为$$ {{{\boldsymbol{R}}}_{{{xx}}}} = {{E}}\left\{ {{{\boldsymbol{x}}}{{{\boldsymbol{x}}}^{\text{H}}}} \right\} = {{\boldsymbol{A}}}{{{\boldsymbol{R}}}_{{{ss}}}}{{{\boldsymbol{A}}}^{\text{H}}} + {{\boldsymbol{b}}}\sigma _{{v}}^2{{{\boldsymbol{b}}}^{\text{H}}} + {\sigma _{{n}}}^2{{\boldsymbol{I}}} $$ (12) 式中,
$ \sigma _{{v}}^2 $ 是欺骗信号的功率.欺骗信号中每颗卫星信号的功率与真实信号功率相当,但由于多颗卫星的虚假信号从同一方向入射到天线阵列,而真实卫星信号从不同方向入射到天线阵列,欺骗信号的功率可以在空域上累积,故欺骗信号的空间功率密度远远大于真实信号的空间功率密度[29-30]. 对接收信号协方差矩阵进行特征值分解,得到
$$ {{{\boldsymbol{R}}}_{{{xx}}}} \approx \left[ {{{\boldsymbol{b}}}\quad{{\boldsymbol{U}}}} \right]\left[ {\begin{array}{*{20}{c}} {\sigma _{{v}}^2 + {{\bar \sigma }^2}}&0 \\ 0&{{{\bar \sigma }^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{\boldsymbol{b}}}^{\text{H}}}} \\ {{{{\boldsymbol{U}}}^{\text{H}}}} \end{array}} \right] $$ (13) 式中:
${{\boldsymbol{U}}}$ 为噪声加真实信号子空间的特征向量;${\bar \sigma ^2}$ 为其等效功率. 通过对协方差矩阵的特征值与设定的阈值进行比较,即可判断接收信号中是否存在欺骗干扰[31],其中阈值一般通过恒虚警率(constant false alarm rate, CFAR)方法确定.1.2.2 基于DOA估计的欺骗干扰检测
由1.2.1节介绍的欺骗信号与真实信号的空间特征可知,欺骗信号中不同卫星信号来自同一方向,具有强相关性,这是真实卫星信号所不具备的特征. 故接收信号的DOA特征是一个有效的欺骗干扰检测量,常见的DOA估计方法有Capon法、多重信号分类法(multiple signal classification, MUSIC)、旋转子空间不变法(estimating signal parameter via rotational invariance techniques, ESPRIT)等. 文献[32]将测量得到的卫星导向向量与期望的卫星信号导向向量组成的矩阵进行奇异值分解,比较奇异值之和与阈值的大小来判断接收信号是否异常. 文献[33-34]的思路类似,利用的是欺骗场景中虚假的卫星信号DOA的一致性. 文献[35]先估计每颗卫星信号的DOA,并将其划分到不同的空间信道中. 然后在两个不同的空间通道上进行互相关计算,并监测互相关峰的数量,欺骗干扰与其他信号的互相关结果中会出现多个互相关峰值.
文献[36-38]给出了一种利用接收信号DOA进行欺骗干扰检测的思路. 使用阵列天线可以对信号源进行DOA估计,得到天线坐标系下的波达方向
${{{\boldsymbol{D}}}_{{\text{loc}}}}$ . 而天线阵列在东北天(east-north-up, ENU)坐标系中的姿态往往是未知的,通过接收并解算真实卫星信号,利用卫星历书和星历信息,得到卫星信号的期望DOA值$ {{{\boldsymbol{D}}}_{{\text{ENU}}}} $ ,则:$$ {{{\boldsymbol{D}}}_{{\text{ENU}}}} = {{\boldsymbol{R}}}{{{\boldsymbol{D}}}_{{\text{loc}}}} + {{\boldsymbol{N}}} $$ (14) 式中:旋转矩阵
${{\boldsymbol{R}}} \in SO\left( 3 \right)$ ,$SO(3)$ 为$ {{\mathbb{R}}^{3 \times 3}} $ 空间中的旋转群;${{\boldsymbol{N}}}$ 为观测噪声. 天线的姿态可以通过外加传感器进行辅助确定,文献[39]使用惯性测量单元和里程计与天线阵列组合,进行天线阵列定姿.欺骗干扰检测问题可以与天线阵列定姿问题联合起来
$$ (\hat r,\hat p,\hat y) = \mathop {\arg \min }\limits_{r,p,y} {\left\| {{{\boldsymbol{R}}}(r,p,y){{{\boldsymbol{D}}}_{{\text{ENU}}}} - {{{\boldsymbol{D}}}_{{\text{loc}}}}} \right\|^2} $$ (15) 式中:
$r$ 为横滚角;$p$ 为俯仰角;$y$ 为偏航角. 使用天线姿态解的误差平方和(sum of squares due to error, SSE)作为检测量$$ {\text{SSE}} = {{\mathrm{trace}}} \left\{ {{{{\boldsymbol{Q}}}^{\text{T}}}{{\boldsymbol{R}}}_{{N}}^{ - 1}{{\boldsymbol{Q}}}} \right\}. $$ (16) 式中:
$ {{\boldsymbol{Q}}} = {{\boldsymbol{R}}}(r,p,y){{{\boldsymbol{D}}}_{{\text{ENU}}}} - {{{\boldsymbol{D}}}_{{\text{loc}}}} $ ;${{{\boldsymbol{R}}}_{{N}}}$ 为测量噪声的协方差矩阵. 文献[36]证明在没有欺骗的情况下,由式(16)定义的${\text{SSE}}$ 无偏且零均值,服从自由度$k = 2{N_{{\text{DOA}}}} - 3$ 的中心卡方分布,其中${N_{{\text{DOA}}}}$ 为测得的卫星${\text{DOA}}$ 数目. 而在欺骗场景下,天线阵列测量得到的卫星信号DOA与期望的卫星DOA不一致,${\text{SSE}}$ 有偏,服从非中心卡方分布,自由度与无欺骗场景下的自由度相同.对信号中是否存在欺骗干扰进行假设检验,以式(16)定义的
${\text{SSE}}$ 为检测量,根据Neyman-Pearson准则在设定的虚警率下确定检测阈值,当检测量大于阈值时判断信号中存在欺骗干扰.1.2.3 基于CNR差分的欺骗干扰检测
卫星信号的CNR是容易获得的导航原始观测量信息,是一种有效识别信号异常能量电平的特征量. 传统的信号强度监测方法通过识别信号CNR的突变和连续性来判断信号是否异常. 但是在压制干扰和欺骗干扰同时存在的场景,压制干扰会抬升背景噪声水平,欺骗干扰会增加GNSS信号功率,导致CNR保持在一个稳定的水平,传统方法性能下降.
文献[40]提出了一种载噪比单差(CNR single difference, CSD)度量,两颗不同卫星之间的CSD度量表示为
$$ \Delta {C_{h,l}} = \left| {{C_h} - {C_l}} \right| $$ (17) 式中,
${C_h}$ 和${C_l}$ 分别为第$h$ 和第$l$ 颗卫星的CNR. 在没有欺骗信号的场景下,有$$ \Delta C_{h,l}^{{\text{au}}} = \frac{{{C_s}{{\left| {A\left( {\theta _l^{{\text{au}}},\varphi _l^{{\text{au}}}} \right)} \right|}^2}(b - 1){{\left| {\displaystyle\int_{ - \tfrac{{{\beta _r}}}{2}}^{\tfrac{{{\beta _r}}}{2}} {\displaystyle\sum\limits_{m = 1}^M {{W_m}} } (f){G_s}(f){\text{d}}f} \right|}^2}}}{{\displaystyle\int_{ - \tfrac{{{\beta _r}}}{2}}^{\tfrac{{{\beta _r}}}{2}} {G_w^{}} (f){G_s}(f){\text{d}}f}} $$ (18) 式中:
${C_s}$ 为入射信号的功率;$ A\left( {\theta _l^{{\text{au}}},\varphi _l^{{\text{au}}}} \right) $ 为天线阵元对来自$ \left( {\theta _l^{{\text{au}}},\varphi _l^{{\text{au}}}} \right) $ 方向入射信号的响应;$ b = \left( {{{\left| {A\left( {\theta _h^{{\text{au}}},\varphi _h^{{\text{au}}}} \right)} \right|}^2}/} {{\left| {A\left( {\theta _l^{{\text{au}}},\varphi _l^{{\text{au}}}} \right)} \right|}^2} \right) $ 为天线阵元对第$h$ 颗和$l$ 颗卫星响应的差异;${\;\beta _r}$ 为射频前端以零点为中心的带宽;$M$ 为天线阵元数;${W_m}(f)$ 为射频前端的信道响应;${G_s}(f)$ 为信号的归一化功率谱密度;${G_w}(f)$ 为天线阵列输出端的干扰加噪声的功率谱密度. 可以看出在欺骗信号不存在的场景下,不同卫星之间的CSD度量由阵列因子和噪声特性决定. 而在欺骗场景中,由于欺骗信号来自于同一方向,所以有$$ b = \left( {{{\left| {A\left( {\theta _h^{{\text{au}}},\varphi _h^{{\text{au}}}} \right)} \right|}^2}/{{\left| {A\left( {\theta _l^{{\text{au}}},\varphi _l^{{\text{au}}}} \right)} \right|}^2}} \right) = 1 $$ (19) 则
$$ \Delta C_{h,l}^{sp} = 0. $$ (20) 由于观测噪声影响,欺骗信号的CSD度量不会严格为0,但是否存在欺骗信号对CSD度量的影响很大,故CSD度量也是一个有效的欺骗干扰检测量. 通过与设定的阈值对比即可判断接收信号中是否存在欺骗干扰.
1.3 欺骗干扰抑制
阵列天线可以对每个天线阵元的相位和振幅进行精确控制,形成特定方向的波束,这给欺骗干扰抑制提供了有效的工具. 目前常见的欺骗干扰抑制方法是子空间投影技术和波束成形技术.
1.3.1 子空间投影
由于欺骗信号的空间功率密度远大于真实信号的空间功率密度,对接收信号的协方差矩阵做特征值分解,其最大特征值对应的特征向量张成的空间即为欺骗信号的子空间,通过式(13)得到欺骗信号子空间
${{\boldsymbol{b}}}$ ,通过调整天线阵元的加权向量${{\boldsymbol{f}}}$ 可以使得天线方向图在欺骗信号的方位产生零陷[27],则$$ {\boldsymbol{f}}^{\text{H}}{\boldsymbol{b}}=0, \Vert {\boldsymbol{f}}^{\text{H}}\Vert \ne 0 $$ (21) 为了求解满足式(21)的
${{\boldsymbol{f}}}$ ,计算欺骗信号子空间的正交空间$$ {{{\boldsymbol{P}}}_ \bot } = {{\boldsymbol{I}}} - {{\boldsymbol{b}}}{\left( {{{{\boldsymbol{b}}}^{\text{H}}}{{\boldsymbol{b}}}} \right)^{ - 1}}{{{\boldsymbol{b}}}^{\text{H}}} $$ (22) 则加权向量
$$ {{\boldsymbol{f}}} = {{{\boldsymbol{P}}}_ \bot }{{\boldsymbol{h}}} $$ (23) 其中
${{\boldsymbol{h}}}$ 为任意向量,且$\left\| {{\boldsymbol{h}}} \right\| = 1$ . 可以证明$$ \begin{split} {{{\boldsymbol{f}}}^{\text{H}}}{\boldsymbol{b}} &={{{\boldsymbol{h}}}^{\text{H}}}{\left( {{{{\boldsymbol{P}}}_ \bot }} \right)^{\text{H}}}{{\boldsymbol{b}} = }{{{\boldsymbol{h}}}^{\text{H}}}{{{\boldsymbol{P}}}_ \bot }{{\boldsymbol{b}}} \\ &= {{{\boldsymbol{h}}}^{\text{H}}}\left( {{{\boldsymbol{I}}} - {{\boldsymbol{b}}}{{\left( {{{{\boldsymbol{b}}}^{\text{H}}}{{\boldsymbol{b}}}} \right)}^{ - 1}}{{{\boldsymbol{b}}}^{\text{H}}}} \right){{\boldsymbol{b}}} \\ &= {{{\boldsymbol{h}}}^{\text{H}}}\left( {{{\boldsymbol{b}}} - {{\boldsymbol{b}}}{{\left( {{{{\boldsymbol{b}}}^{\text{H}}}{{\boldsymbol{b}}}} \right)}^{ - 1}}{{{\boldsymbol{b}}}^{\text{H}}}{{\boldsymbol{b}}}} \right) = 0 \end{split} $$ (24) 对接收信号在
${{{\boldsymbol{P}}}_ \bot }$ 上投影,得到欺骗干扰抑制后的信号$$ {{\boldsymbol{r}} = }{{{\boldsymbol{P}}}_ \bot }{{\boldsymbol{x}}} $$ (25) 1.3.2 波束成形
通过调整天线各阵元权值,使阵列方向图主瓣对准期望信号,并对干扰实现有效抑制,这一过程称为波束形成(beamforming, BF),最优波束形成的寻优准则有最大信干噪比(maximum signal to inter-ference plus noise ratio, MSINR)准则、最小均方误差准则(minimum mean square error, MMSE)准则、最小方差无失真响应(minimum variance distor-tionless response, MVDR)准则、线性约束最小方差 (linearly constrained minimum variance,LCMV) 准则等.
文献[34]给出了一种基于LCMV的欺骗干扰抑制方法. 假设已经估计出欺骗信号的DOA和真实信号的DOA,假设有
$K$ 个真实卫星信号受到单个欺骗源欺骗,则可以得到式(8)中的导向矩阵:$$ {{\boldsymbol{A}}}(\theta ) = \left[ {{{{\boldsymbol{a}}}_{sp}}({\theta _{sp}}),{{\boldsymbol{a}}}({\theta _1}),{{\boldsymbol{a}}}({\theta _2}),\cdots,{{\boldsymbol{a}}}({\theta _K})} \right] $$ (26) 式中:
$ {{{\boldsymbol{a}}}_{sp}}({\theta _{sp}}) $ 代表DOA为$ {\theta _{sp}} $ 时欺骗信号的导向向量;$\left[ {{\theta _1},{\theta _2},\cdots,{\theta _K}} \right]$ 为真实卫星信号的DOA. 则约束向量$$ {g} = {\left[ {0,\underbrace {1,1,\cdots,1}_K} \right]^{\text{T}}} $$ (27) 天线阵列输出端信号
$$ {{\boldsymbol{y}} = }{{{\boldsymbol{w}}}^{\text{H}}}{{\boldsymbol{x}}} $$ (28) 式中,
${{\boldsymbol{w}}}$ 为天线阵元的加权因子. 解优化问题$$ \left\{ {\begin{array}{*{20}{l}} {\mathop {\min }\limits_{\boldsymbol{w}} {{{\boldsymbol{w}}}^{\text{H}}}{{{\boldsymbol{R}}}_{{{xx}}}}{{\boldsymbol{w}}}} \\ {\text{s.t.}\;{{{\boldsymbol{w}}}^{\text{H}}}{{\boldsymbol{A}}} = {{{\boldsymbol{g}}}^{\text{H}}}} \end{array}} \right. $$ (29) 得到最佳的波束形成权向量
$$ {{{\boldsymbol{w}}}_{{\text{LCMV}}}} = {{\boldsymbol{R}}}_{{{xx}}}^{ - 1}{{\boldsymbol{A}}}{\left( {{{{\boldsymbol{A}}}^{\text{H}}}{{\boldsymbol{R}}}_{{{xx}}}^{ - 1}{{\boldsymbol{A}}}} \right)^{ - 1}}{{\boldsymbol{g}}} $$ (30) 根据式(28)即可得到欺骗干扰抑制后的信号.
2. 稀疏阵列防欺骗技术
均匀阵列接收信号之间有冗余的相位信息,并没有完全利用其阵列孔径. 稀疏阵列通过合理的阵列构型,在相同的天线阵元数的情况下,拥有更大的阵列孔径和自由度,能够解决均匀阵列在信号源数大于天线阵元数的场景下估计性能不佳的问题. 在相同阵列孔径的情况下,稀疏阵列所需的物理天线数要少于均匀线阵. 这意味着更少的天线单元数目需求,相应的信号接收系统和处理系统的规模也会减小,从而极大地降低设备成本.
2.1 稀疏阵列构型
稀疏阵列将一个阵列划分为多个均匀子阵,根据子阵之间阵元间距的关系以及如何将子阵合成为一个阵列可以设计出不同的稀疏阵列[41-45],常用的稀疏阵列构型分为互质阵列和嵌套阵列两类[46].
2.1.1 互质线阵
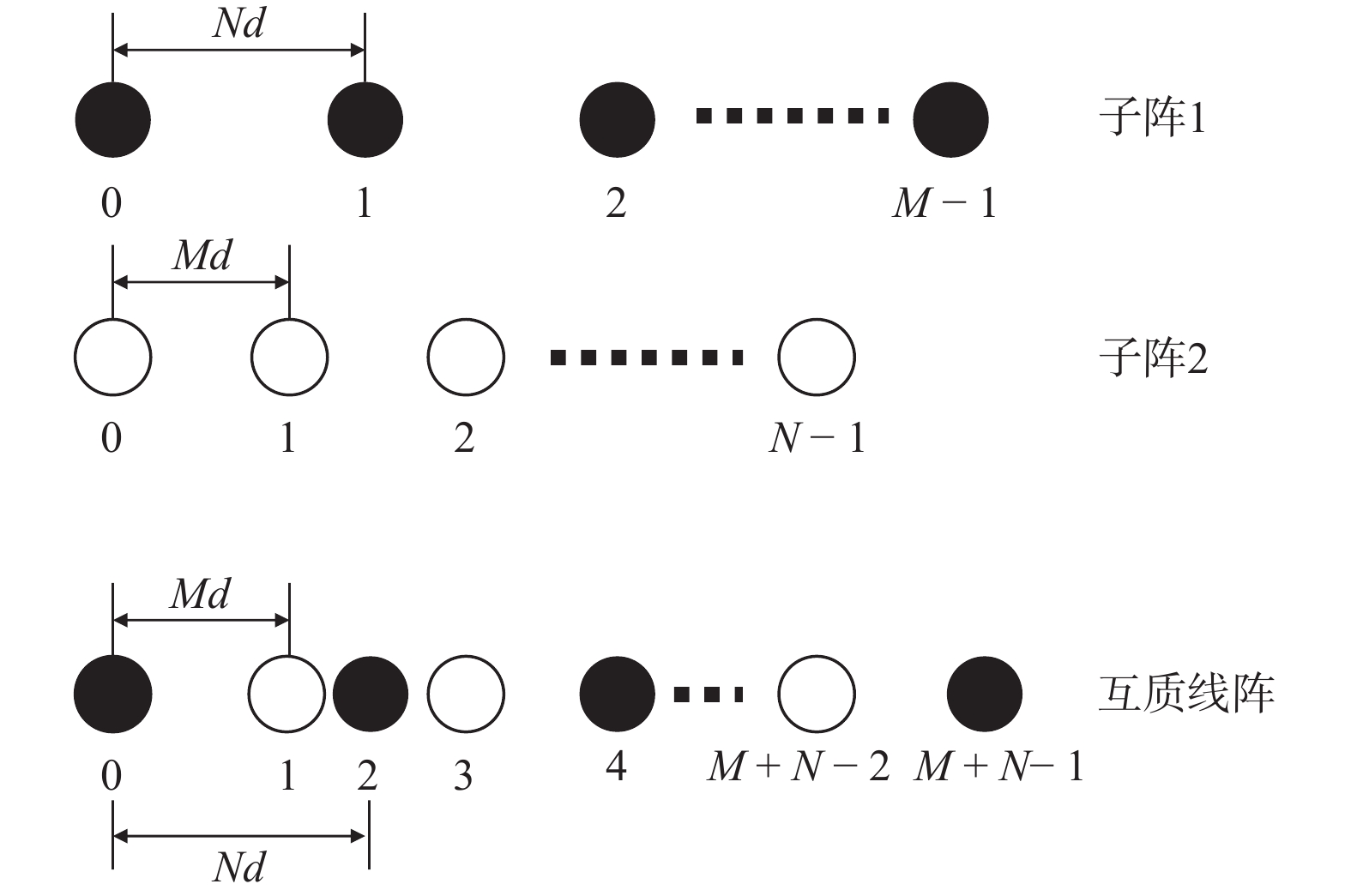
如图2所示,互质线阵由两个均匀线阵构成的子阵组成,子阵1中包含了
$M$ 个均匀分布的阵元,阵元间距为$Nd$ ,子阵2中包含了$N$ 个均匀分布的阵元,阵元间距为$Md$ ,其中$d$ 为信号半波长,且$M$ 和$N$ 互质. 两个子阵均以原点为参考点,则阵元位置可记为$$ \mathbb{L}=\left\{mNd|0\leqslant m\leqslant M-1\right\}\cup \left\{nMd|0\leqslant n\leqslant N-1\right\} $$ (31) 此时,两个子阵的导向向量分别为:
$$ {{{\boldsymbol{a}}}_1}({\theta _k}) = {\left[ {1,{{\text{e}}^{ - \frac{{{\text{j}}2{\text{π }}Nd\sin \;{\theta _k}}}{\lambda }}},\cdots,{{\text{e}}^{ - \frac{{{\text{j}}2{\text{π }}(M - 1)Nd \sin \;{\theta _k}}}{\lambda }}}} \right]^{\text{T}}} $$ (32) $$ {{{\boldsymbol{a}}}_2}({\theta _k}) = {\left[ {1,{{\text{e}}^{ - \frac{{{\text{j2π}}Md\sin \;{\theta _k}}}{\lambda }}},\cdots,{{\text{e}}^{ - \frac{{{\text{j}}2{\text{π}}(N - 1)Md \sin \;{\theta _k}}}{\lambda }}}} \right]^{\text{T}}} $$ (33) 定义互质线阵的导向向量和方向矩阵为:
$$ {{\boldsymbol{a}}}({\theta _k}) = {\left[ {{{{\boldsymbol{a}}}_{1}^{\text{T}}}({\theta _k}),{{{\boldsymbol{a}}}_{2}^{\text{T}}}({\theta _k})} \right]^{\text{T}}} $$ (34) $$ {{\boldsymbol{A}}} = \left[ {{{\boldsymbol{a}}}({\theta _1}),{{\boldsymbol{a}}}({\theta _2}),\cdots,{{\boldsymbol{a}}}({\theta _K})} \right] $$ (35) 由式(7)和式(10)可得到接收信号的协方差矩阵
$ {{{\boldsymbol{R}}}_{{{xx}}}} $ ,对$ {{{\boldsymbol{R}}}_{{{xx}}}} $ 进行向量化,得到$$ \begin{split} {\boldsymbol{z}} &= {\mathrm{vec}}\left\{ {{{{\boldsymbol{R}}}_{{{xx}}}}} \right\} \\ &= \left( {{{{\boldsymbol{A}}}^ * } \otimes {{\boldsymbol{A}}}} \right){\mathrm{vec}}\left\{ {{{{\boldsymbol{R}}}_{{{ss}}}}} \right\} + \sigma _{{n}}^2{\mathrm{vec}}\left\{ {{\boldsymbol{I}}} \right\} \\ &= \left( {{{{\boldsymbol{A}}}^ * } \odot {{\boldsymbol{A}}}} \right){{\boldsymbol{p}} + }\sigma _{{n}}^2{{{\boldsymbol{I}}}_{{n}}} \end{split} $$ (36) 式中:
${\mathrm{vec}}\left\{ \cdot \right\}$ 为向量化操作;$ \otimes $ 为kronecker积;$ \odot $ 为Khatri-Rao积;$ {{\boldsymbol{p}} = }{\left[ \sigma _{1}^{2},\sigma _{2}^{2},\cdots,\sigma _{K}^{2} \right]^{\text{T}}} $ 是由信号功率组成的向量;$ {{{\boldsymbol{I}}}_{{n}}} = {{\mathrm{vec}}} \left\{ {\boldsymbol{I}} \right\} $ . 记$B = {{{\boldsymbol{A}}}^{\text{H}}} \odot {{\boldsymbol{A}}}$ ,则$$ {\boldsymbol{z}} = \boldsymbol{B}\boldsymbol{p} +\sigma _{n}^{2}{\boldsymbol{I}_{n}} $$ (37) 可以将
${{\boldsymbol{p}}}$ 视为单快拍的信号向量,则${{\boldsymbol{z}}}$ 即为${{\boldsymbol{p}}}$ 由方向矩阵为${{\boldsymbol{B}}}$ 的天线阵列接收到的信号.方向矩阵
${{\boldsymbol{B}}}$ 中第$k$ 列${{\boldsymbol{b}}}\left( {{\theta _k}} \right)$ 包含的相位信息为$$ {\text{e}}^{-\frac{\text{j}2\text{π}({l}_{i}-{l}_{j})d\;{\mathrm{sin}}\;{\theta }_{k}}{\lambda }},{l}_{i},{l}_{j}\in \mathbb{L} $$ (38) 式中,
$\lambda $ 为信号波长. 记$$ \mathbb{D}=\left\{l_{i}-l_{j} \mid l_{i}, l_{j} \in \mathbb{L}\right\} $$ (39) 称阵元位置集合为
${\mathbb{D}}$ 的阵列为该互质阵列的差联合阵列,又称该阵列经过虚拟化得到的虚拟阵列. 假设阵列由$M$ 个阵元组成,则其虚拟阵列的空间自由度最大能达到$$ {\text{DO}}{{\text{F}}_{{\text{coprime}}}}{{ = }}M(M - 1) + 1 $$ (40) 即使虚拟阵列中的元素可能存在冗余,使得实际空间自由度略小于式(40),但对比均匀阵列,互质线阵极大的提高了空间自由度,使其由
$O(M)$ 提高到了$O({M^2})$ .2.1.2 嵌套线阵
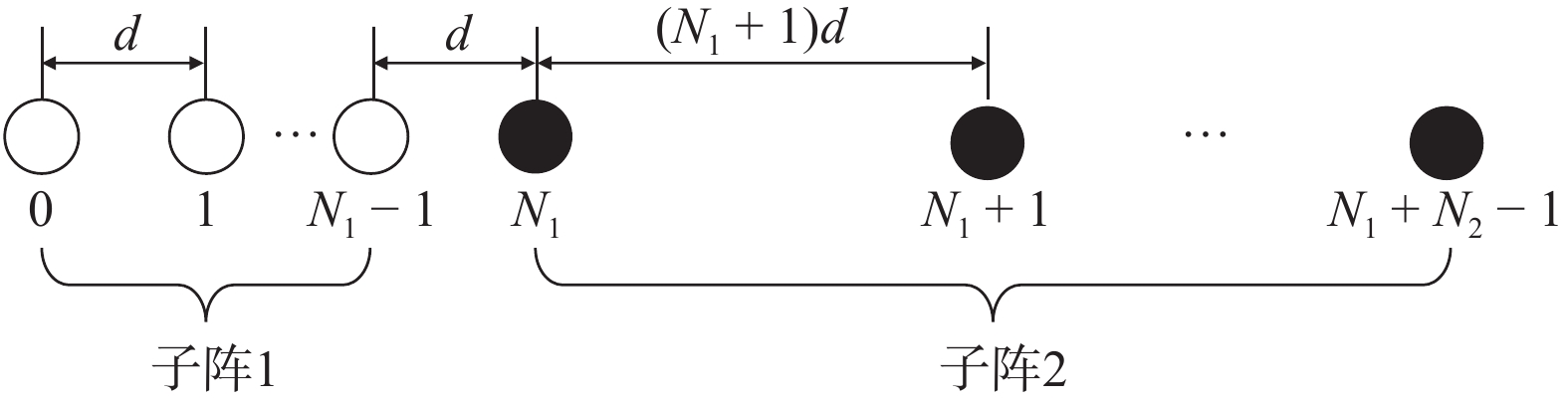
嵌套线阵由两个或两个以上阵元间距不同的均匀线阵串联而成,若子阵
$i$ 包含${N_i}$ 个阵元,阵元间距为$d$ ,则下一级子阵阵元间距为$\left( {{N_i} + 1} \right)d$ . 对于超过二级的嵌套线阵,其虚拟阵列不是完全的均匀阵列. 本小节以二级嵌套线阵为例,其结构如图3所示,其中子阵$1$ 阵元数为${N_1}$ ,子阵$2$ 阵元数为${N_2}$ ,则阵元位置可以记为$$ \begin{split}\mathbb{L}=&\left\{md|0\leqslant m\leqslant {N}_{1}-1\right\}\cup \\ &\left\{{N}_{1}d+n({N}_{1}+1)d|0\leqslant n\leqslant {N}_{2}-1\right\}\end{split} $$ (41) 则两个子阵的导向向量分别为:
$$ {{{\boldsymbol{a}}}_1}\left( {{\theta _k}} \right) = {\left[ {1,{{\text{e}}^{ - \frac{{{\text{j}}2{\text{π}}d\;{\mathrm{sin}}\;{\theta _k}}}{\lambda }}}\cdots,{{\text{e}}^{ - \frac{{{\text{j}}2{\text{π}}({N_1} - 1)d\;{\mathrm{sin}}\;{\theta _k}}}{\lambda }}}} \right]^{\text{T}}} $$ (42) $$ {{{\boldsymbol{a}}}_2}\left( {{\theta _k}} \right) = {\left[ {{{\text{e}}^{ - \frac{{{\text{j}}2{\text{π}}{N_1}d\;{\mathrm{sin}}\;{\theta _k}}}{\lambda }}},{{\text{e}}^{ - \frac{{{\text{j2π}}({N_1} + ({N_1} + 1))d\;{\mathrm{sin}}\;{\theta _k}}}{\lambda }}},\cdots,{{\text{e}}^{ - \frac{{{\text{j2π}}({N_1} + ({N_2} - 1)({N_1} + 1))d \sin \;{\theta _k}}}{\lambda }}}} \right]^{\text{T}}} $$ (43) 定义嵌套线阵的导向向量和方向矩阵为:
$$ {{\boldsymbol{a}}}({\theta _k}) = {\left[ {{{{\boldsymbol{a}}}_{1}^{\text{T}}}({\theta _k}),{{{\boldsymbol{a}}}_{2}^{\text{T}}}({\theta _k})} \right]^{\text{T}}} $$ (44) $$ {{\boldsymbol{A}}} = \left[ {{{\boldsymbol{a}}}({\theta _1}),{{\boldsymbol{a}}}({\theta _2}), \cdots ,{{\boldsymbol{a}}}({\theta _K})} \right] $$ (45) 同2.1.1节推导,我们可以得到嵌套线阵的虚拟阵列阵元位置为
$$ \begin{split}\mathbb{D}&=\left\{{l}_{i}-{l}_{j}|{l}_{i},{l}_{j}\in \mathbb{L}\right\}\\& =\left\{nd|n=-{N}_{2}({N}_{1}+1)+1,{\cdots},{N}_{2}({N}_{1}+1)-1\right\}\end{split} $$ (46) 即二级的嵌套线阵的虚拟阵列是一个有
$ 2{N_2} ({N_1} + 1) - 1 $ 个阵元,阵元间距为$d$ 的均匀线阵,式(36)~(38)同样适用于嵌套线阵. 嵌套线阵的空间自由度由${N_1}$ 和${N_2}$ 决定,假设$$ N = {N_1} + {N_2} $$ (47) 最优的二级嵌套线阵的布阵方式如下:
1) 当
$N$ 为偶数,且$ {N_1} = {N_2} = \dfrac{N}{2} $ 时$$ {\text{DO}}{{\text{F}}_{{\text{nested}}}} = \frac{{{N^2} - 2}}{2} + N $$ (48) 2) 当
$N$ 为奇数,且${N_1} = \dfrac{{N - 1}}{2},{N_2} = \dfrac{{N + 1}}{2}$ 时$$ {\text{DO}}{{\text{F}}_{{\text{nested}}}} = \frac{{{N^2} - 1}}{2} + N $$ (49) 2.2 稀疏阵列防欺骗
稀疏阵列将均匀阵列的空间自由度从
$O(M)$ 提高到了$O({M^2})$ ,在相同天线孔径的条件下,大大降低了阵列天线的成本. 稀疏阵列同样是阵列天线的一种,适用于均匀阵列的防欺骗技术理论上都可以应用于稀疏阵列. 其中欺骗抑制的方法与1.3节一致,故本小节主要介绍如何利用稀疏阵列进行欺骗干扰检测.2.2.1 基于功率异常的欺骗干扰检测
由1.2.1节知,欺骗信号的空间功率密度远大于真实信号的空间功率密度. 体现在接收信号的协方差矩阵上,就是其特征值分解会出现一个显著的较大值,反应了欺骗信号的功率. 文献[47]提出了利用互质阵列进行功率监测的欺骗干扰检测方法. 采用拓展的互质阵列进行接收信号,具体的阵列构型,如表2所示.
表 2 互质阵列构型子阵 阵元数 阵元间距 1 $2{M_1}$ ${M_2}d$ 2 ${M_2}$ ${M_1}d$ 根据2.1.1节可得到虚拟阵列接收信号
${{\boldsymbol{z}}}$ ,但是由于虚拟的发射信号${{\boldsymbol{p}}}$ 各个分量之间是相干的,导致虚拟阵列接收信号的协方差矩阵秩降为1,为了解决这个问题,去掉矩阵${{\boldsymbol{B}}}$ 中的重复行,并对剩余行进行排序,得到矩阵$ {{{\boldsymbol{B}}}_{{I}}} $ ,其行与阵元数$ {S_{{I}}} = 2{M_1}{M_2} + 2{M_1} - 1 $ 的均匀阵列相同,进而得到新的虚拟阵列接收信号$$ {{{\boldsymbol{z}}}_{{I}}} = {{{\boldsymbol{B}}}_{{I}}}{{\boldsymbol{p}}} + \sigma _{{n}}^2{{{\boldsymbol{I}}}_{{n}}} $$ (50) 则一个满秩的协方差矩阵可以直接得出:
$$ {{{\boldsymbol{R}}}_{{v}}} = \left[ {\begin{array}{*{20}{l}} {{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{{L_{{I}}}}}}&{{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{{L_{{I}}} - 1}}}& \cdots &{{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_1}} \\ {{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{{L_{{I}}} + 1}}}&{{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{{L_{{I}}}}}}& \cdots &{{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_2}} \\ \;\;\;\; \vdots & \;\;\;\;\vdots & \; & \;\;\;\vdots \\ {{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{2{L_{{I}}} - 1}}}&{{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{2{L_{{I}}} - 2}}}& \cdots &{{{\left( {{{{\boldsymbol{z}}}_{{I}}}} \right) }_{{L_{{I}}}}}} \end{array}} \right] $$ (51) 式中,
$ {\left\langle {{{{\boldsymbol{z}}}_{{I}}}} \right\rangle _q} $ 为$ {{{\boldsymbol{z}}}_{{I}}} $ 的第$q$ 个元素,虚拟阵列等效的天线阵元数为$ {L_{{I}}} = ({S_{{I}}} + 1)/2 $ . 由于新构造的协方差矩阵自由度降低,通过拓展矩阵的方法增加天线阵列的自由度,得到协方差矩阵${{{\boldsymbol{R}}}_{{\text{aug}}}}$ . 通过对${{{\boldsymbol{R}}}_{{\text{aug}}}}$ 进行奇异值分解,得到$K$ 个奇异值${S_p}(p = 1,2,...,K)$ ,其中$K$ 代表入射信号的个数. 使用最小二乘的方法对$K$ 个奇异值进行拟合,并且使用${\text{SSE}}$ 评估解的质量:$$ {\text{SSE}} = \sum\limits_{p = 1}^K {{{\left( {{S_p} - {{\bar S}_p}} \right)}^2}} $$ (52) 式中,
${\bar S_p}$ 为${S_p}$ 的拟合值. 该${\text{SSE}}$ 在不存在欺骗的场景和存在欺骗的场景服从不同的非中心卡方分布${\chi ^2}(K,\lambda )$ ,其中$\lambda $ 依赖于入射信号的功率. 将${\text{SSE}}$ 作为欺骗干扰的检测量,与设定的阈值比较即可判断接收信号中是否存在欺骗干扰.2.2.2 基于DOA估计的欺骗干扰检测
与均匀阵列接收信号有所不同,稀疏阵列的虚拟阵列接收信号
${{\boldsymbol{p}}}$ 是相干的,所以不能直接应用传统的DOA估计算法去测量稀疏阵列接收信号的DOA. 可以通过对虚拟信号进行解相干处理,再应用经典的DOA估计算法,或者通过压缩感知和稀疏重构的方法,从单快拍的接收数据中获取需要的DOA信息.1) 基于解相干的DOA估计方法
空间平滑算法是一种有效的解相干算法,可以解决传统DOA估计技术在信号源相干情况下性能下降的问题. 如图4所示,将
$M$ 元等距线阵用前向滑动的方式分成$L$ 个$K$ 元子阵,其中$L = M - K + 1$ ,假设$d = \lambda /2$ ,则全阵时接收信号$$ {{\boldsymbol{x}}}(n) = {{\boldsymbol{A}}}(\theta ){{\boldsymbol{s}}}(n) + {{\boldsymbol{n}}}(n) $$ (53) 其中导向向量
$$ {{\boldsymbol{a}}}(\theta ) = \left[ {1,{{\text{e}}^{ - {\text{jπsin}}\;\theta }},\cdots,{{\text{e}}^{ - {\text{j}}(M - 1){\text{πsin}}\;\theta }}} \right] $$ (54) 第
$l$ 个子阵的接收信号$$ {{{\boldsymbol{x}}}_l}(n) = {{{\boldsymbol{A}}}_K}(\theta ){{{\boldsymbol{D}}}^{l - 1}}{{\boldsymbol{s}}}(n) + {{{\boldsymbol{n}}}_l}(n),l = 1,2,\cdots,L $$ (55) 式中,
${{\boldsymbol{D}}} = {\text{diag}}\{ {{\text{e}}^{{\text{jπsin}} \;{\theta _1}}},{{\text{e}}^{{\text{jπsin}} \;{\theta _2}}},\cdots,{{\text{e}}^{{\text{jπsin}} \;{\theta _P}}}\} $ ,其中$P$ 代表信源个数. 将多个子阵数据在相关域进行平均$$ \begin{split} {{{\tilde {\boldsymbol{R}}}}_L} &= \frac{1}{L}\sum\limits_{l = 1}^L {{{{\boldsymbol{R}}}_l}} \\ &= {{{\boldsymbol{A}}}_K}\left[ {\frac{1}{L}\sum\limits_{l = 1}^L {{{{\boldsymbol{D}}}^{l - 1}}{{{\boldsymbol{R}}}_{ss}}} {{{\boldsymbol{D}}}^{ - (l - 1)}}} \right]{{\boldsymbol{A}}}_K^{\text{H}} + \sigma _n^2{{\boldsymbol{I}}} \\ & ={{{\boldsymbol{A}}}_K}{{{\tilde {\boldsymbol{R}}}}_S}{{\boldsymbol{A}}}_K^{\text{H}} + \sigma _n^2{{\boldsymbol{I}}} \end{split} $$ (56) 式中,
${{\tilde {\boldsymbol{R}}}_S} = \displaystyle\frac{1}{L}\sum\limits_{l = 1}^L {{{{\boldsymbol{D}}}^{l - 1}}{{{\boldsymbol{R}}}_{ss}}} {{{\boldsymbol{D}}}^{ - (l - 1)}}$ .通过在相关域做平均的方法,可以提高
${{\tilde {\boldsymbol{R}}}_S}$ 的秩,从而达到解相干的效果. 当平滑次数$L$ 越大时,解相关效果越好,但是此时子阵的阵元数$K$ 也减小,造成了孔径损失. 对虚拟阵列接收数据进行空间平滑解相干后,就可以使用传统的MUSIC、ESPRIT等算法进行DOA估计,进而使用1.2.2节的方法进行欺骗干扰检测.2) 基于压缩感知的DOA估计方法
一般而言,信源数远小于空域网格划分数,故接收信号在空域上是稀疏的,可以对接收信号进行稀疏表示,再根据压缩感知的原理使用测量矩阵对信号进行重构. 空间平滑可以有效的对信号进行解相干,但是会损失阵列孔径,而压缩感知可以在不损失阵列孔径的情况下实现对信号的DOA估计.
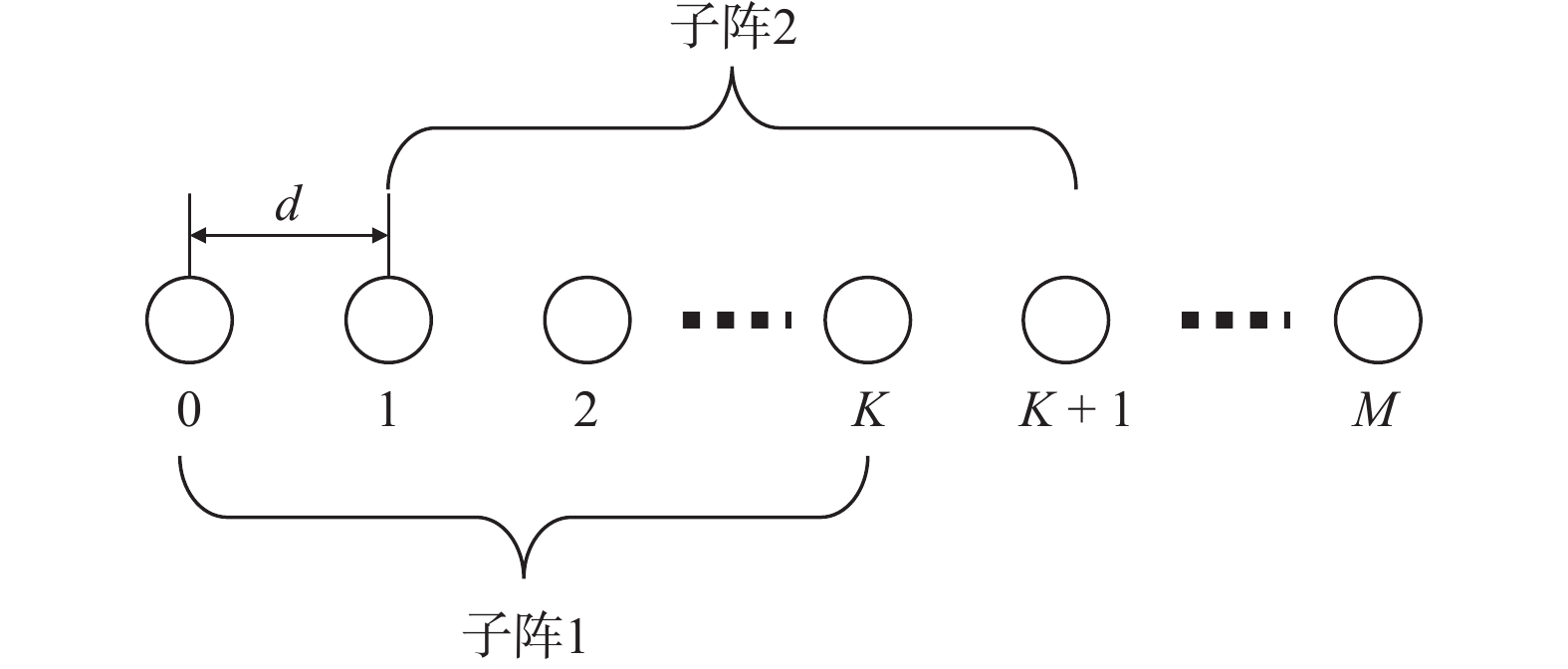
文献[48]给出了一种利用压缩感知对稀疏阵列接收信号进行DOA估计的思路. 对于阵元位置为
${\mathbb{L}}$ 的稀疏阵列,其接收信号$$ {{{\boldsymbol{x}}}_{\mathbb{L}}}(t) = {{{\boldsymbol{A}}}_{\mathbb{L}}}{{\boldsymbol{s}}}(t) + {{\boldsymbol{v}}}(t) $$ (57) 式中:
$ {{{\boldsymbol{A}}}_{\mathbb{L}}} $ 为稀疏阵列的导向矩阵;${{\boldsymbol{v}}}(t)$ 为高斯白噪声. 使用观测矩阵${{\boldsymbol{\varPhi}} } \in {{\mathbb{C}}^{M \times L}}$ 作用于接收信号,其中$L$ 是虚拟阵元个数,$M$ 是输出向量维度,得到输出信号$$ \begin{split} {{\boldsymbol{y}}}(t) &= {{\boldsymbol{\varPhi}} }{{{\boldsymbol{x}}}_{\mathbb{L}}}(t) + {{\boldsymbol{w}}}(t) \\ & = {{\boldsymbol{\varPhi}} }{{{\boldsymbol{A}}}_{\mathbb{L}}}{{\boldsymbol{s}}}(t) + {{\boldsymbol{n}}}(t) \end{split} $$ (58) 式中:
${{\boldsymbol{w}}}(t)$ 为观测网络带来的噪声;$ {{\boldsymbol{n}}}(t) = {{\boldsymbol{\varPhi}} {\boldsymbol{v}}}(t) + {{\boldsymbol{w}}}(t) $ 是总的噪声. 输出信号的协方差矩阵为$$ \begin{split} {{{\boldsymbol{R}}}_{{{yy}}}} &= {E} \left\{ {{{\boldsymbol{y}}}(t){{\boldsymbol{y}}}{{(t)}^{\text{H}}}} \right\} \\ &= {{\boldsymbol{\varPhi}} }{{{\boldsymbol{A}}}_{\mathbb{L}}}{{{\boldsymbol{R}}}_{{{ss}}}}{{\boldsymbol{A}}}_{\mathbb{L}}^{\text{H}}{{{\boldsymbol{\varPhi}} }^{\text{H}}} + {{{p}}_{{v}}}{{\boldsymbol{\varPhi}} }{{{\boldsymbol{\varPhi}} }^{\text{H}}} + {{{p}}_{{w}}}{{{\boldsymbol{I}}}_M} \\ \end{split} $$ (59) 式中:
$ {{{p}}_{{v}}} $ 和$ {{{p}}_{{w}}} $ 分别是${{\boldsymbol{v}}}(t)$ 和${{\boldsymbol{w}}}(t)$ 的功率. 对式(59)进行向量化,得到$$ \begin{split} {{{\boldsymbol{r}}}_{{{yy}}}} =& {{\mathrm{vec}}} \left( {{{{\boldsymbol{R}}}_{{{yy}}}}} \right) \\ = &\left( {{{{\boldsymbol{\varPhi}} }^ * } \otimes {{\boldsymbol{\varPhi}} }} \right)\left( {{{\boldsymbol{A}}}_{\mathbb{L}}^ * \odot {{{\boldsymbol{A}}}_{\mathbb{L}}}} \right){{\boldsymbol{p}}} \\ &+ {{{p}}_{{v}}}\left( {{{{\boldsymbol{\varPhi}} }^ * } \otimes {{\boldsymbol{\varPhi}} }} \right){{\mathrm{vec}}} ({{{\boldsymbol{I}}}_L}) + {{{p}}_{{w}}}{\mathrm{vec}} ({{{\boldsymbol{I}}}_M}) \\ =& {{\boldsymbol{\varPsi b}}} \end{split} $$ (60) 式中
$$ {{\boldsymbol{\varPsi}} = }\left[ {\left( {{{{\boldsymbol{\varPhi}} }^ * } \otimes {{\boldsymbol{\varPhi}} }} \right)\left( {{{\boldsymbol{A}}}_{\mathbb{L}}^ * \odot {{{\boldsymbol{A}}}_{\mathbb{L}}}} \right),\left( {{{{\boldsymbol{\varPhi}} }^ * } \otimes {{\boldsymbol{\varPhi}} }} \right){{\mathrm{vec}}} ({{{\boldsymbol{I}}}_L}),{{\mathrm{vec}}} ({{{\boldsymbol{I}}}_M})} \right] $$ (61) $$ {{\boldsymbol{b}}} = {\left[ {{{{\boldsymbol{p}}}^{\text{T}}},{p_{{v}}},{p_{{w}}}} \right]^{\text{T}}} $$ (62) 将空域划分为若干个网格,即
$$ {{{\boldsymbol{\theta}} }^{\left( g \right)}} = {\left[ {\theta _1^{\left( g \right)},\theta _2^{\left( g \right)},\cdots ,\theta _G^{\left( g \right)}} \right]^{\text{T}}} $$ (63) 式中,
$G$ 为划分的网格数,且$G \gg Q$ ,其中$Q$ 为信源数. 可以得到一个由$G$ 个元素组成的稀疏向量p°,其中仅有$Q$ 个非零元素,代表了信源的DOA. 网格化后,有:$$ {{{\boldsymbol{\varPsi}} }^{\left( g \right)}}{ = }{\left[ {\begin{array}{*{20}{c}} {\left( {{{{\boldsymbol{\varPhi}} }^ * } \otimes {{\boldsymbol{\Phi}} }} \right)\left( {{{\left( {{{\boldsymbol{A}}}_{\mathbb{L}}^{\left( g \right)}} \right)}^ * } \odot {{\boldsymbol{A}}}_{\mathbb{L}}^{\left( g \right)}} \right)} \\ {\left( {{{{\boldsymbol{\varPhi}} }^ * } \otimes {{\boldsymbol{\varPhi}} }} \right){\mathrm{vec}} ({{{\boldsymbol{I}}}_L})} \\ {{{\mathrm{vec}}} ({{{\boldsymbol{I}}}_M})} \end{array}} \right]^{\text{T}}} $$ (64) $$ {{{\boldsymbol{b}}}\text{°} } = {\left[ {{{{\boldsymbol{p}}}\text{°} }^{\text{T}},{p_{{v}}},{p_{{w}}}} \right]^{\text{T}}} $$ (65) 则DOA估计问题可以转化为以下约束问题:
$$ \left\{ {\begin{array}{*{20}{c}} {{{{\tilde {\boldsymbol{b}}}}\text{°} } = \arg \mathop {\min }\limits_{{{{\boldsymbol{b}}}\text{°} }} {{\left\| {{{{\boldsymbol{b}}}\text{°} }} \right\|}_0}} \\ {\text{s.t.}{\text{ }}{{\left\| {{\boldsymbol{r}_{{{yy}}}} - {{{\boldsymbol{\varPsi}} }^{\left( g \right)}}{{{\boldsymbol{b}}}\text{°} }} \right\|}_2} < \varepsilon } \end{array}} \right. $$ (66) 一种求解方法是最小绝对值收敛和选择算子算法(least absolute shrinkage and selection operator al-gorithm, LASSO),其目标函数为
$$ {{\tilde {\boldsymbol{b}}}\text{°} } = \arg \mathop {\min }\limits_{{{{\boldsymbol{b}}}\text{°} }} \left[ {\frac{1}{2}{{\left\| {{\boldsymbol{r}_{{{yy}}}} - {{{\boldsymbol{\varPsi}} }^{\left( g \right)}}{{{\boldsymbol{b}}}\text{°} }} \right\|}_2} + \eta {{\left\| {{{{\boldsymbol{b}}}\text{°} }} \right\|}_1}} \right] $$ (67) 式中:
$\eta $ 为正则化参数;$ {{\tilde {\boldsymbol{b}}}\text{°} } $ 反映了接收信号的DOA. 得到信号的DOA估计后,使用1.2.2节的方法进行欺骗干扰检测.3. 结束语
本文根据天线阵列构型的不同,从均匀阵列和稀疏阵列两个方向介绍了基于阵列天线信号处理的防欺骗技术. 欺骗信号中各颗卫星的虚假信号经过相同的信道到达接收机,导致信号之间具有强相关性,这是真实信号所不具备的特征. 欺骗干扰检测的本质是对接收信号物理特征如空间功率密度、DOA、CNR等的相关性进行评估. 而欺骗干扰抑制技术,就是在实现检测后,根据得到的欺骗源信息,构造出欺骗源信号子空间的正交空间,利用正交投影技术在欺骗源方向上放置零陷. 但这种处理方式往往会造成期望信号的功率损失,在不能容忍期望信号功率降低的场景中,更经常使用波束成形技术,在抑制欺骗干扰的同时保证期望信号方向上的功率最大,以提高PNT性能.
日益增加的欺骗干扰案例展现了欺骗干扰独特的危害性,如何进行更好的防欺骗,弥补GNSS信号的脆弱性,提高GNSS的安全性和可靠性,是建设综合PNT体系的一个难题. 目前防欺骗干扰技术的难题主要有:
1) 欺骗干扰技术复杂化. 目前的欺骗干扰技术已经不仅仅局限于单个欺骗源,内部之间高同步的多欺骗源干扰技术对传统防欺骗技术带来了新的挑战.
2) 防欺骗干扰技术成本高. 防欺骗技术往往需要使用额外器件如阵列天线、IMU等进行辅助,并对原有接收机结构进行改变,高成本是防欺骗技术目前没有广泛应用的一个很大的影响因素.
未来的防欺骗技术,应该聚焦于提性能、降成本,尽量减少对接收机结构的更改,实现用户无感. 可能的发展趋势如下:
1) 搭建联合防欺骗框架. 针对日益复杂的欺骗技术,单一的针对某个物理特征的防欺骗技术可能满足不了对抗的要求. 搭建联合检测和抑制框架,利用各个子系统之间的互补性,实现更稳健、更鲁棒的防欺骗效果.
2) 发展稀疏阵列防欺骗技术. 在相同的物理孔径下,稀疏阵列使用远低于均匀阵列的天线阵元数就可以达到相近甚至更优的防欺骗效果,极大地降低了阵列天线的成本. 但是目前稀疏阵列的应用尚不成熟,如何设计对物理孔径损失更少的解相干算法,以及设计更匹配的观测矩阵进行压缩感知是未来的研究难题.
3) 实现用户无感的系统设计. 现有防欺骗技术往往需要对用户接收机架构做很大更改,设计尽量不更改原有接收机结构的防欺骗技术,才能在市场化方向上占据优势. 这要求防欺骗技术更专注于GNSS信号解扩前的物理特征. 在捕获前实现防欺骗,就能将防欺骗功能做成独立的功能模块嵌入到接收机中,减少对系统的更改.
-
表 1 GNSS防欺骗技术
项目 信息层 信号层 单天线 阵列天线 辅助传感器 检测 伪距、
伪距残差、
多普勒-钟飘双差等CNR、
载波相位、
相关峰、
矢量接收机等信号强度、
DOA等IMU、
高度计等抑制 信号加密认证 MLE、AGC等 功率倒置、
波束形成、
子空间投影、
空时自适应处理等- 表 2 互质阵列构型
子阵 阵元数 阵元间距 1 $2{M_1}$ ${M_2}d$ 2 ${M_2}$ ${M_1}d$ -
[1] 明锋, 曾安敏. 弹性PNT最新进展及相关问题研究[J]. 导航定位学报, 2022, 10(4): 1-10. [2] OPSGROUP. FAA warning issued, further serious navigation failures reported[EB/OL]. (2023-09-28)[2024-01-10]. https://ops.group/blog/faa-warning-navigation-failures
[3] ORIANA P, MAGGIE M. Israel’s using widespread GPS tampering to deter Hezbollah’s missiles[EB/OL]. (2023-10-23)[2024-01-10]. https://www.politico.com/news/2023/10/23/israels-gps-tampering-deter-hezbollahs-missiles-00123026
[4] CHEN Z K, LI J, WENG Q Z, et al. An BDS spoofing interference detection and identification method using the radio determination satellite service[C]//Joint Confer-ence of the European Frequency and Time Forum and IEEE International Frequency Control Symposium (EFTF/IFCS). IEEE, 2023: 1-5. DOI: 10.1109/EFTF/IFCS57587.2023.10272130
[5] KHANAFSEH S, ROSHAN N, LANGEL S, et al. GPS spoofing detection using RAIM with INS coupling[C]// IEEE/ION Position, Location and Navigation Sympos-ium-PLANS, 2014: 1232-1239. DOI: 10.1109/PLANS.2014.6851498
[6] SWASZEK P F, HARTNETT R J, SEALS K C. GNSS spoof detection using independent range information[C]// International Technical Meeting of the Institute of Navigation, 2016: 739-747. DOI: 10.33012/2016.13457
[7] WU Q A, CUI X, LU M Q, et al. A GNSS anti-spoofing technique based on the spatial distribution characteristic of the residual vectors[J]. Tsinghua science and technol-ogy, 2023, 29(2): 457-468. DOI: 10.26599/tst.2023.9010017
[8] WANG Z X, ZHANG X M, ZHOU Z H, et al. GNSS spoofer localization for vehicles based on doppler and clock drift double difference[J]. IEEE transactions on vehicular technology, 2022, 72(4): 4466-4481. DOI: 10.1109/TVT.2022.3226528
[9] LI J, CHEN Z K, RAN Z G, et al. The GNSS spoofing detection method based on adaboost[C]//The 6th International Symposium on Autonomous Systems (ISAS). IEEE, 2023: 1-6. DOI: 10.1109/ISAS59543.2023.10164411
[10] WESSON K D, ROTHLISBERGER M P, HUMPHREYS T E. A proposed navigation message authentication implementat-ion for civil GPS anti-spoofing[C]//The 24th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2011), 2011: 3129-3140. DOI: 10.15781/T2J679D0V
[11] HUMPHREYS T E, BHATTI J A, SHEPARD D P, et al. The texas spoofing test battery: toward a standard for evaluating GPS signal authentication techniques[C]//Radionavigat-ion Laboratory Conference Proceedings, 2012. DOI: 10.15781/T26D5PT4X
[12] CHENG X J, XU J N, CAO K J, et al. An authenticity verification scheme based on hidden messages for current civilian GPS signals[C]//The 4th International Conference on Computer Sciences and Convergence Information Technology, 2009: 345-352. DOI: 10.1109/ICCIT.2009.91
[13] 邓旭, 吕志伟, 周玟龙, 等. 采用载噪比的卫星导航欺骗检测算法设计[J]. 导航定位学报, 2022, 10(2): 109-118. [14] DEHGHANIAN V, NIELSEN J, LACHAPELLE G. GNSS spoofing detection based on receiver C/N0 estimates[C]//The 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012), 2012: 2878-2884.
[15] 耿正霖, 聂俊伟, 李柏渝, 等. 多方位测量的相位双差GNSS欺骗干扰检测算法[J]. 国防科技大学学报, 2016, 38(3): 32-38. DOI: 10.11887/j.cn.201603006 [16] PHELTS R E. Multicorrelator techniques for robust mitigation of threats to GPS signal quality[M]. Stanford University, 2001.
[17] MUBARAK O M, DEMPSTER A G. Performance comparison of ELP and DELP for multipath detection[C]//The 22nd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2009), 2009: 1074-1081.
[18] SHANG X Y, SUN F P, WANG D M, et al. GNSS spoofing detection based on multi-correlator distortion monitoring[J]. GPS solutions, 2023, 27(2): 94. DOI: 10.1007/s10291-023-01438-0
[19] SUN C, CHEONG J W, DEMPSTER A G, et al. Robust spoofing detection for GNSS instrumentation using Q-channel signal quality monitoring metric[J]. IEEE transactions on instrumentation and measurement, 2021(70): 1-15. DOI: 10.1109/TIM.2021.3102753
[20] ZHOU W L, LV Z W, WU W B, et al. Anti-spoofing technique based on vector tracking loop[J]. IEEE transactions on instrumentation and measurement, 2023(72): 1-16. DOI: 10.1109/TIM.2023.3289551
[21] 贾琼琼, 朱传胜. 基于多通道SQM指标联合的矢量接收机多径干扰检测方法[J]. 全球定位系统, 2023, 48(3): 110-119. [22] 周志健, 冉承新, 戴志强, 等. GNSS直接位置估计技术综述[J]. 全球定位系统, 2023, 48(2): 10-21. DOI: 10.12265/j.gnss.2022199 [23] WANG F, LI H, LU M Q. GNSS spoofing detection and mitigation based on maximum likelihood estimation[J]. Sensors, 2017, 17(7): 1532. DOI: 10.3390/s17071532
[24] AKOS D M. Who’s afraid of the spoofer? GPS/GNSS spoofing detection via automatic gain control (AGC)[J]. Navigation:journal of the institute of navigation, 2012, 59(4): 281-290. DOI: 10.1002/navi.19
[25] BROUMANDAN A, JAFARNIA-JAHROMI A, DANESHMAND S, et al. Overview of spatial processing approaches for GNSS structural interference detection and mitigation[J]. Proceedings of the IEEE, 2016, 104(6): 1246-1257. DOI: 10.1109/JPROC.2016.2529600
[26] TANIL C, KHANAFSEH S, PERVAN B. GNSS spoofing attack detection using aircraft autopilot response to deceptive trajectory[C]//The 28th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2015). 2015: 3345-3357.
[27] TANIL Ç, KHANAFSEH S, JOERGER M, et al. An INS monitor to detect GNSS spoofers capable of tracking vehicle position[J]. IEEE transactions on aerospace and electronic systems, 2017, 54(1): 131-143. DOI: 10.1109/TAES.2017.2739924
[28] 徐奕禹, 陈长风, 袁雪林, 等. 基于高度计辅助的GNSS欺骗干扰检测[J/OL]. (2022-01-13)[2024-01-10]. 系统工程与电子技术. http://kns.cnki.net/kcms/detail/11.2422.TN.20221207.1452.004.html [29] DANESHMAND S, JAFARNIA-JAHROMI A, BROUMANDON A, et al. A low-complexity GPS anti-spoofing method using a multi-antenna array[C]//The 25th international technical meeting of the satellite division of the institute of navigation (ION GNSS 2012), 2012: 1233-1243. DOI: 10.1007/978-3-642-22078-4_43
[30] DANESHMAND S, JAFARNIA-JAHROMI A, BROUMANDAN A, et al. A GNSS structural interference mitigation technique using antenna array processing[C]//IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), 2014: 109-112.
[31] ZHANG J, CUI X, XU H, et al. A two-stage interference suppression scheme based on antenna array for GNSS jamming and spoofing[J]. Sensors, 2019, 19(18): 3870. DOI: 10.3390/s19183870
[32] APPEL M, KONOVALTSEV A, MEURER M. Robust spoofing detection and mitigation based on direction of arrival estimation[C]//The 28th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS+ 2015), 2015: 3335-3344.
[33] 王璐, 吴仁彪, 王文益, 等. 基于多天线的GNSS压制式干扰与欺骗式干扰联合抑制方法[J]. 电子与信息学报, 2016, 38(9): 2344-2350. [34] MAGIERA J. A multi-antenna scheme for early detection and mitigation of intermediate GNSS spoofing[J]. Sensors, 2019, 19(10): 2411. DOI: 10.3390/s19102411
[35] ZHAO Y Q, SHEN F, XU G H, et al. A spatial-temporal approach based on antenna array for GNSS anti-spoofing[J]. Sensors, 2021, 21(3): 929. DOI: 10.3390/s21030929
[36] MEURER M, KONOVALTSEV A, CUNTZ M, et al. Robust joint multi-antenna spoofing detection and attitude estimation using direction assisted multiple hypotheses RAIM[C]//The 25th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2012), 2012: 3007-3016.
[37] KONOVALTSEV A, CUNTZ M, HAETTICH C, et al. Autonomous spoofing detection and mitigation in a GNSS receiver with an adaptive antenna array[C]//The 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), 2013: 2937-2948. DOI: 10.1109/PLANS46316.2020.9109842
[38] KONOVALTSEV A, CUNTZ M, HAETTICH C, et al. Performance analysis of joint multi-antenna spoofing detection and attitude estimation[C]//The 2013 International Technical Meeting of The Institute of Navigation. 2013: 864-872. DOI: 10.1117/12.2028852
[39] VAGLE N, BROUMANDAN A, LACHAPELLE G. Multiantenna GNSS and inertial sensors/odometer coupling for robust vehicular navigation[J]. IEEE internet of things journal, 2018, 5(6): 4816-4828. DOI: 10.3390/s18051305
[40] LIU J Y, CHEN F, XIE Y, et al. Robust spoofing detection for GNSS array instrumentation based on C/N0 difference measurements[J]. IEEE transactions on instrumentation and measurement, 2023(72): 1-11.
[41] WANG X R, ABOUTANIOS E, DEMPSTER A G. Low cost adaptive array signal processing by subarray selection[C]//IGNSS 2013, 2013.
[42] WANG X R, ABOUTANIOS E, TRINKLE M, et al. Reconfigurable adaptive array beamforming by antenna selection[J]. IEEE transactions on signal processing, 2014, 62(9): 2385-2396. DOI: 10.1109/TSP.2014.2312332
[43] SHI W, VOROBYOV S A, LI Y. ULA fitting for sparse array design[J]. IEEE transactions on signal processing, 2021(69): 6431-6447. DOI: 10.1109/TSP.2021.3125609
[44] SHAIKH A H, DANG X, HUANG D. DOA estimation using antenna arrays: a universal array designing frame-work[J]. IEEE transactions on vehicular technology, 2023, 72(11): 15092-15097.
[45] ZHOU C W, GU Y J, SHI Z G, et al. Structured nyquist correlation reconstruction for DOA estimation with sparse arrays[J]. IEEE transactions on signal processing, 2023(71): 1849-1862. DOI: 10.1109/TSP.2023.3251110
[46] 张小飞, 李建峰, 徐大专, 等. 阵列信号处理及MATLAB实现[M]. 北京: 电子工业出版社, 2020: 305-308. [47] ZHAO Y Q, SHEN F, XU D J, et al. A coprime array-based technique for spoofing detection and DOA estimation in GNSS[J]. IEEE sensors journal, 2022, 22(23): 22828-22835. DOI: 10.1109/JSEN.2022.3211024
[48] GUO M, ZHANG Y D, CHEN T. DOA estimation using compressed sparse array[J]. IEEE transactions on signal processing, 2018, 66(15): 4133-4146. DOI: 10.1109/TSP.2018.2847645
-
期刊类型引用(0)
其他类型引用(1)



 下载:
下载: