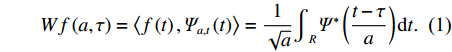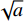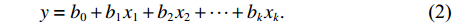Soil moisture model of Inner Mongolia based on GNSS ZTD and meteorological elements
-
摘要: 土壤水含量是农牧业衡量干旱的重要指标,对气候生态具有重要影响,土壤水的变化趋势对于区域的水土流失和气候变化研究等工作具有重要意义,而我国对于土壤水含量的监测起步较晚,因此有必要利用其他已有数据开展土壤水含量模型研究. 利用内蒙古已有全球导航卫星系统(GNSS)天顶对流层延迟(ZTD)数据和湿度、日照以及蒸发量数据进行土壤水含量反演模型研究. 首先将各要素与土壤水含量进行相关性分析,因土壤水含量与GNSS ZTD数据均存在观测噪声,所以应对数据进行去噪处理. 利用小波变换方法剔除噪声,去噪后土壤水含量数据与各要素相关性均有所提高,土壤水含量与湿度相关性最好,两者各实验点的平均相关性为0.645;土壤水含量与日照和蒸发量呈负相关,其平均相关性分别为−0.561、−0.547;而土壤水含量与GNSS ZTD数据相关性最小,其平均相关性为0.271. 根据各要素与土壤水含量的相关性,进行土壤水含量模型构建并进行可靠性验证. 经验证误差统计发现:实验区域NMWJ站模型精度最高,其精度为90.1%;HLAR站点模型精度最低,其精度为69.1%;各站点的平均精度为81.35%. 基于多变量要素的土壤水含量模型可为土壤水含量的趋势变化研究提供参考,通过研究土壤水含量的变化趋势,对区域进行水资源的合理分配利用从而达到节约水资源目的.
-
关键词:
- 土壤水含量 /
- 反演 /
- 全球导航卫星系统(GNSS) /
- 天顶对流层延迟(ZTD) /
- 气象要素 /
- 内蒙古
Abstract: Soil water content is an important indicator of drought in agriculture and animal husbandry, and has an important impact on climate and ecology. The change trend of soil water is of great significance for regional soil erosion and climate change research. But monitoring of soil water content in China is lagging. Thus, soil water content should be investigated using other existing data. In this study, the existing Global Navigation Satellite System (GNSS) zenith tropospheric delay (ZTD) and humidity, sunshine, and evaporation data in Inner Mongolia was used to investigate soil water content inversion. The correlation between each element and soil water content was analyzed. Noises was observed in the soil water content and GNSS ZTD data. Wavelet transform was used to eliminate the noises. After denoising, the correlation between soil water content data and each element was improved, and the correlation between soil water content and humidity is the best. The average correlation between the two experimental points is 0.645. Negative correlations are observed between soil water content and sunshine and evaporation, and their average correlations are −0.561 and −0.547, respectively. The correlation between soil water content and GNSS ZTD data is the smallest, with an average correlation of 0.271. Then, a soil water content model was constructed on the basis of the correlation between each element and soil water content, and its reliability was verified. The verified error statistics show that the NMWJ station model in the experimental area has the highest accuracy, with the accuracy of 90.1%, whereas the HLAR site model has the lowest accuracy, with 69.1%. The average accuracy of each station in the study area is 81.35%. The soil water content model based on multivariable elements can provide reference for the research on the change trend of soil water content. Reasonable distribution and utilization of water resources in the region can be conducted through the research on the change trend of soil water content to conserve water resources. -
0. 引 言
土壤水含量是农业和畜牧业等领域衡量土壤干旱水平的重要指标,对气候、生态、水文有十分重要的影响. 通过对土壤水含量的监测,以及分析土壤水含量的变化趋势能够预测未来的变化状况,对水资源进行有效地分配,以及水土资源的可持续利用,对于生态环境的保护和农畜业旱情的监测等都具有重要的意义.
目前土壤水含量的监测方法主要有传统物理监测方法、基于全球导航卫星系统反射测量(GNSS-R)的土壤水含量反演、基于空间遥感技术的土壤水含量反演和基于数理统计模型计算的土壤水含量模拟. 传统物理监测具有土层多、深度大、精度高等特点,但需人工野外采集样本,所需人力物力财力较大,很难大范围及时长效的监测土壤水含量,故该种方法多用于其他方法反演土壤水含量精度的标定. 基于GNSS-R技术反演土壤水含量[1],该方法精度较高,但是需在测量区域进行布站设点,需耗费大量人力物力,且在野外很难保证长时间的连续观测. 而基于空间遥感的方法反演土壤水主要为光学遥感和微波遥感[2],精度高易获得[3],但光学遥感易受天气和日照影响,而微波遥感易受植被覆盖和地表粗糙度影响,且微波遥感信号易受干扰[4-5]. 第一颗土壤水含量监测卫星为土壤湿度与海洋盐分卫星 (SMOS),该卫星于2009年11月发射[6],数据积累较少不能用于长时序的变化趋势研究工作. 也有相关学者利用重力场来反演某一区域的水储量,但该方法只能反演研究区域的地上水、地下水和土壤水的水储量总量,不能反演研究区域的土壤水含量[7-8],而现有的数理统计模型与概念型模型类模型,一般应用于较小空间尺度,物理机理模型虽然精度较高,但对土壤参数要求较复杂, 所需气象数据较多,不适用于大尺度农田地表土壤水分监测[9-10].
上述获得土壤水含量数据方法均存在问题,不能获得连续的长时序土壤水含量监测数据,因此有必要研究一种新的土壤水含量反演方法,以获得长时序土壤水含量数据,为土壤水含量的变化趋势提供数据支持. 蒸腾蒸发是土壤水消耗的重要因素之一[11-12],土壤水蒸腾蒸发后形成水汽,水汽与土壤水存在相关性[13],全球导航卫星系统(GNSS)天顶对流层延迟(ZTD)主要与气压、温度和水汽含量相关短时间内相同区域气压和温度变化较小,GNSS ZTD变化主要受水汽变化影响,而土壤水与GNSS ZTD存在相关性[14],本文将GNSS ZTD作为反演土壤水的条件之一进行土壤水含量的反演.
本文反演土壤水含量可以为遥感微波反演土壤水含量方法的缺失数据提供参考价值,且GNSS已积累20余年数据,可以利用本文方法进行长时序土壤水含量反演,为土壤水含量的变化趋势研究提供参考价值.
1. 研究数据与数据处理
1.1 研究区域
内蒙古自治区位于中国北部97°12′E~126°04′E,37°24′N~53°23′N,总面积118.3万km2,是中国草原资源最丰富地区之一. 草原荒漠化面积不断增加,生态环境持续恶化,直接威胁到国家生态安全[15],而草地生态系统主要受水资源的影响[16] .
1.2 SMAP土壤水数据
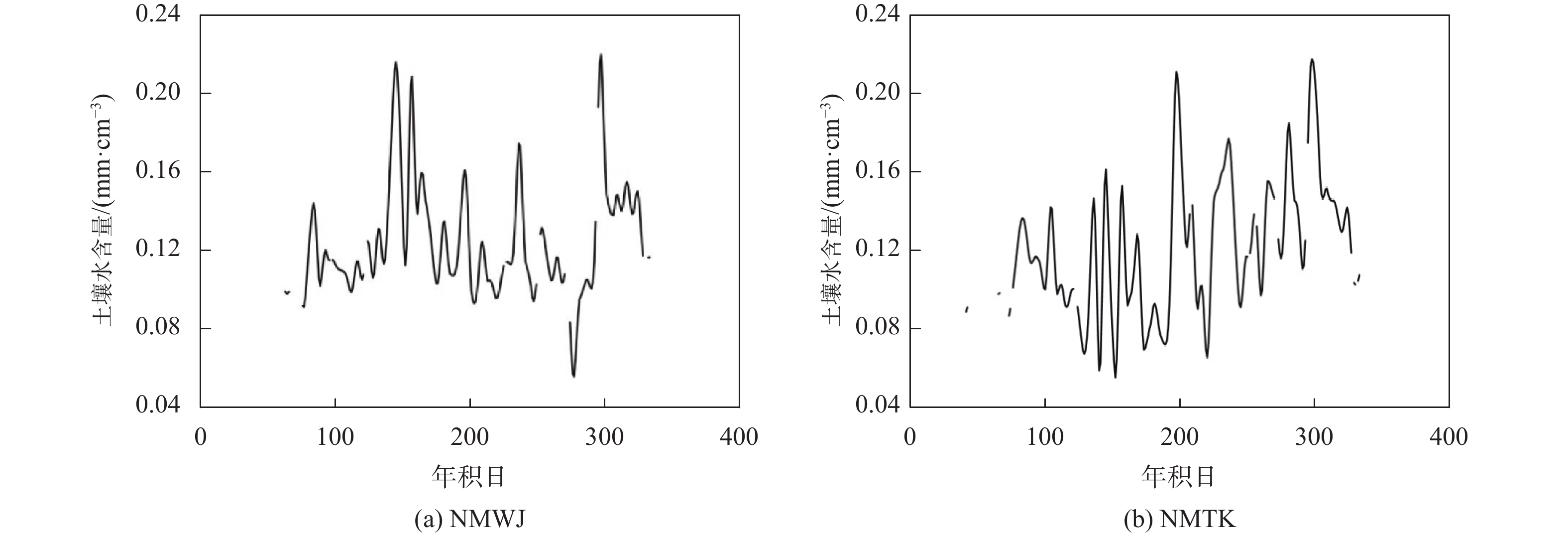
SMAP土壤水含量数据来源于(https://search.earthdata.nasa.gov/),原始数据为9 km格网数据,本文以GNSS站点坐标为中心提取周围18 km的土壤水含量数据进行平均,数据为2016年数据,时间分辨率为2次/日,本文将其平均处理为日均值数据,数据单位为mm/cm3. 图1 为研究区域两站点土壤水含量时间序列.
1.3 GNSS ZTD数据和气象数据
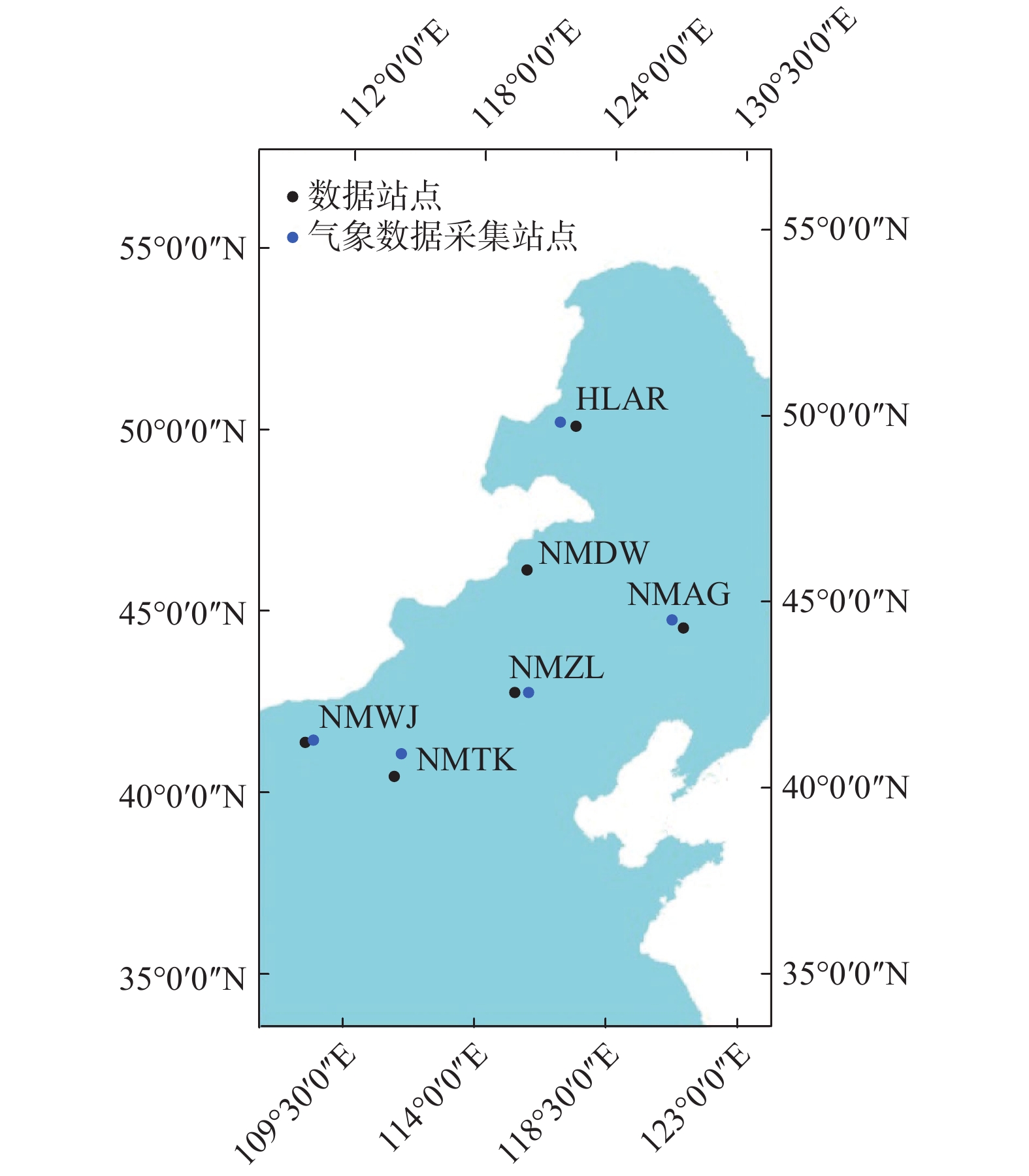
气象数据来源于中国气象共享网站(http://data.cma.cn/),包括0 cm地表温度、日照、相对湿度和蒸发量等要素,各项要素数据为日值数据,时间为2016年数据. 本文实验站点数据采集位置如图2所示.
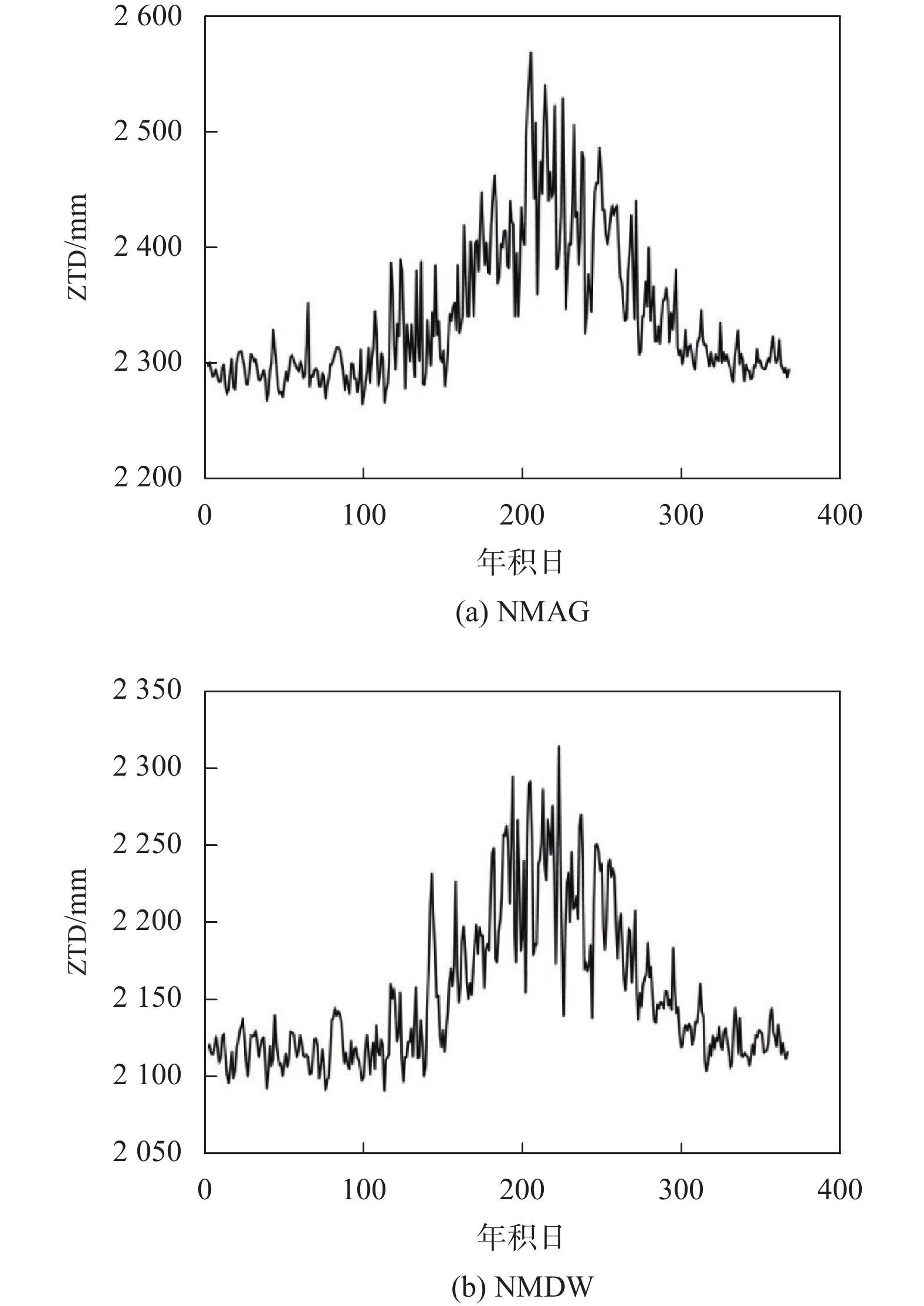
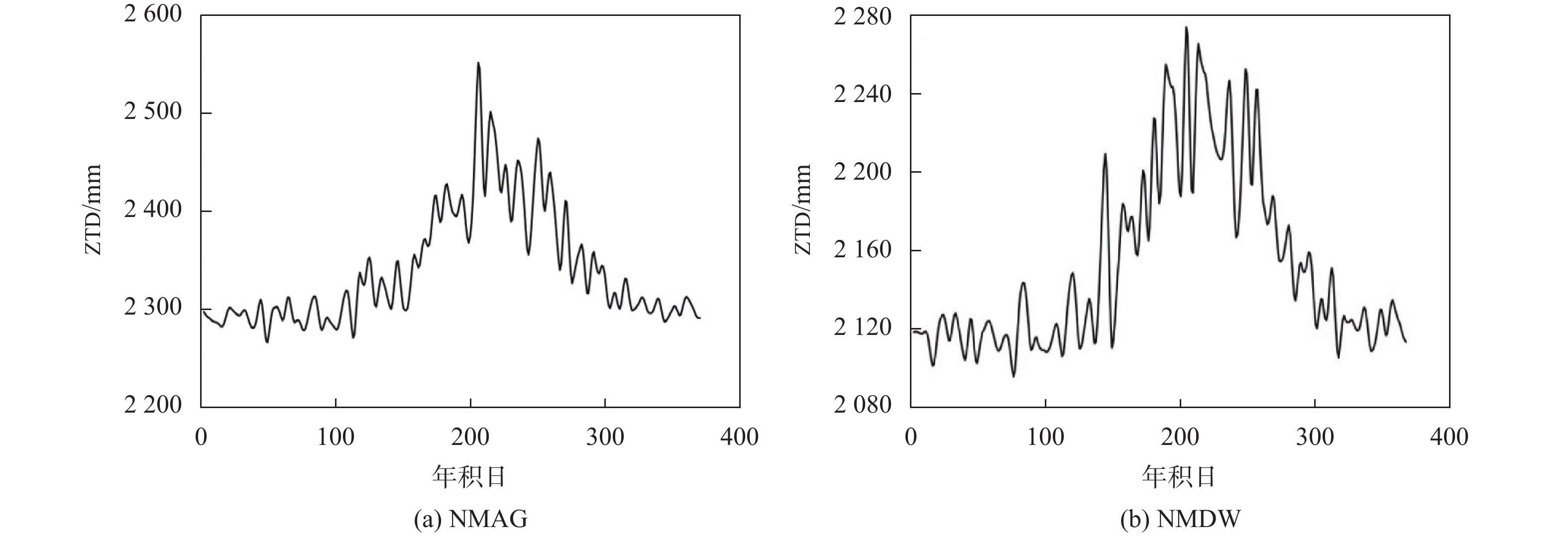
GNSS ZTD数据来源于中国大陆构造环境监测网络(ftp:60.30.77.19/continuousbasicproduct/troposphere), 数据为2016年数据,采集时间分辨率为2 h/次,本文将其平均为日均值,单位为mm. 如图3为实验两站点GNSS ZTD时序变化
如图2为本文选取气象数据采集站点与GNSS站点坐标相吻合站点数据进行研究分析,以保证数据时间和空间的一致性.
2. 研究方法
2.1 小波变换原理
由图3可知,GNSS ZTD序列存在明显的观测噪声,为使各要素与土壤水含量相关性提高,应对各数据进行去噪处理. 本文选用小波去噪方法,小波变换具有高分辨率优点,利用小波变换方法处理数据可以降低噪声造成的影响,可进一步揭示GNSS ZTD变化与土壤水含量之间的关系.
小波变换是一种信号的时间-频率分析方法,具有多分辨分析的特点,而且在时域和频域具有表征信号局部特征的能力. 小波变换是把某一被称为基本小波的函数作位移τ后,在不同尺度a下,与分析信号ƒ(t)做内积
$$ Wf\left(a,\tau \right)=\left\langle{f\left(t\right),{\varPsi }_{a,t}\left(t\right)}\right\rangle=\frac{1}{\sqrt{a}}{\int }_{R}^{}{\varPsi }^{*}\left(\frac{t-\tau }{a}\right)\mathrm{d}t. $$ (1) 式中,a>0为尺度因子,其作用是对基本小波
${\varPsi }_{a,t}\left(t\right)$ 作伸缩,τ反映位移,其值可正可负,a和τ都是连续的变量,故又称为连续小波变换. 在不同的尺度下小波持续时间随值的加大而增宽,幅度则与$ \sqrt{a} $ 反比减少,但波的形状保持不变[17-18].常用的小波函数有Morlet 小波、Marr小波、DOG小波、Haar小波、正交小波等,各小波都有其各自特点. 由于本文需要对大气可降水量(PWV)去噪重构,故选择紧支撑标准正交小波DbN小波系.
2.2 多元线行性回归模型
土壤水含量变化受到多个因素的影响,需要两个或者以上的影响因素作为自变量来解释因变量的变化. 本文利用多个气象要素和GNSS ZTD建立不同多元回归模型反演土壤水含量,并进行精度分析. 设y为因变量,x1,x2,x3,···,xk为自变量,则多元线性回归模型为
$$ y=b_{0}+b_{1}x_{1}+b_{2}x_{2}+\cdots+b_{k}x_{k} . $$ (2) 式中,b0为常数项,b1,b2,···,bk为回归系数.
3. 实验与分析
3.1 土壤水含量与气象要素和GNSS ZTD的相关性比较
气象要素的湿度、日照(辐射)、蒸发量等均能影响土壤水含量. 土壤水含量受渗漏和蒸散等内部因素影响,同时与日照、湿度等外部环境因素相关. 故选择湿度、日照、蒸发量等和GNSS ZTD 与土壤水含量进行相关性分析.
由表1原数据相关性可知,土壤水含量与0 cm地表温度存在相关性具有偶然性,仅3个站点通过相关性显著性检验,且该三个站点的相关性较小,不能证明土壤水含量与0 cm地表温度存在相关性. 土壤水含量与湿度、蒸发量、日照等要素均存在相关性但相关性较小. 结合图1和图3可知,相关性系数较低的原因是GNSS ZTD与土壤水含量之间均存在观测噪声,同时气象要素数据也存在观测噪声. 噪声影响土壤水含量与各要素之间的相关性,会对本文模型构建造成影响,故应对数据进行去噪处理.
表 1 土壤水含量与各要素去噪前后相关性对比站点 原数据相关性 小波分解后相关性 平均相对湿度 日照 蒸发量 GNSS ZTD 0 cm地表温度 平均相对湿度 日照 蒸发量 GNSS ZTD NMDW 0.698 –0.398 –0.511 0.143/0.063 –0.339 0.822 –0.532 –0.691 0.315 NMZL 0.590 –0.401 –0.369 0.386 –0.086/0.279 0.687 –0.515 –0.500 0.389 HLAR 0.593 –0.448 –0.575 0.113/0.163 –0.413 0.650 –0.580 –0.672 –0.192 NMTK 0.498 –0.484 –0.267 0.310 0.175/0.004 0.596 –0.681 –0.420 0.230 NMAG 0.533 –0.496 –0.492 0.329 –0.112/0.101 0.623 –0.594 –0.644 0.375 NMWJ 0.473 –0.431 –0.268 0.198 0.091/0.141 0.493 –0.464 –0.356 0.127/0.040 注:红色字体为显著性值,未标注则其显著性为0.001. 选用小波去噪方法,利用小波变换的方法将GNSS ZTD数据和土壤水含量数据进行分解,剔除噪声层后重构. 由图1与图4、图2与图5对比可知,土壤水含量数据和GNSS ZTD数据经小波变换去噪后,时间序列有明显突变值剔除明显. 而由表1可知,经去噪处理后土壤水含量数据与各要素的相关性均提高,说明噪声对数据相关性有所影响而小波分解重构的方法能够剔除噪声.
由表1可知,NMWJ站土壤水含量与GNSS ZTD数据相关性存在异常,去噪前土壤水含量与GNSS ZTD相关性为0.198,而去噪后其相关性仅为0.127,但两者显著性为0.04<0.05,能够通过显著性检验,证明两者存在统计学相关,GNSS ZTD仍可用于土壤水含量模型构建. 分析造成该情况原因为:该站点GNSS ZTD经小拨分解后其噪声层包含真实数据信息,而小波去噪将其剔除,造成相关性降低.
3.2 不同要素土壤水含量模型构建
因土壤水经蒸腾蒸散作用至大气,所以空气相对湿度与GNSS ZTD (水汽)两种要素可能存在重复. 如表2所示,两者通过显著性检验,存在统计学相关,故作者进行不同模型构建,并检验模型可靠性.
表 2 相对湿度与GNSS ZTD相关性站点 NMAG NMDW HLAR NMTK NMWJ NMZL 相关性 0.754 –0.150 –0.303 0.562 0.335 0.361 注:表2相关性均通过显著性检验. 3.2.1 利用气象要素模型构建
根据表1的相关性分析,仅利用气象要素构建土壤水含量模型. 以土壤水含量为因变量,湿度、日照和蒸发量为自变量构建模型,其中平均相对湿度为百分比数据,本文将其变换为数值数据即:湿度数值数据=湿度数据(%)×0.01. 土壤水含量数据不连续部分数据缺失,为保证精度未将其进行做补缺处理,故数据不为连续数据. 选取数据量的前85%进行构建模型,并用剩余15%数据进行模型的可靠性检验.
表3为利用湿度、日照和蒸发量构建土壤水含量模型的常数项和各要素系数,由表3可知,蒸发量系数较于其他要素系数较小,证明该模型中蒸发量所占比例较小,主要起约束作用. 而湿度系数较大,在该模型中湿度为主要要素为主导作用.
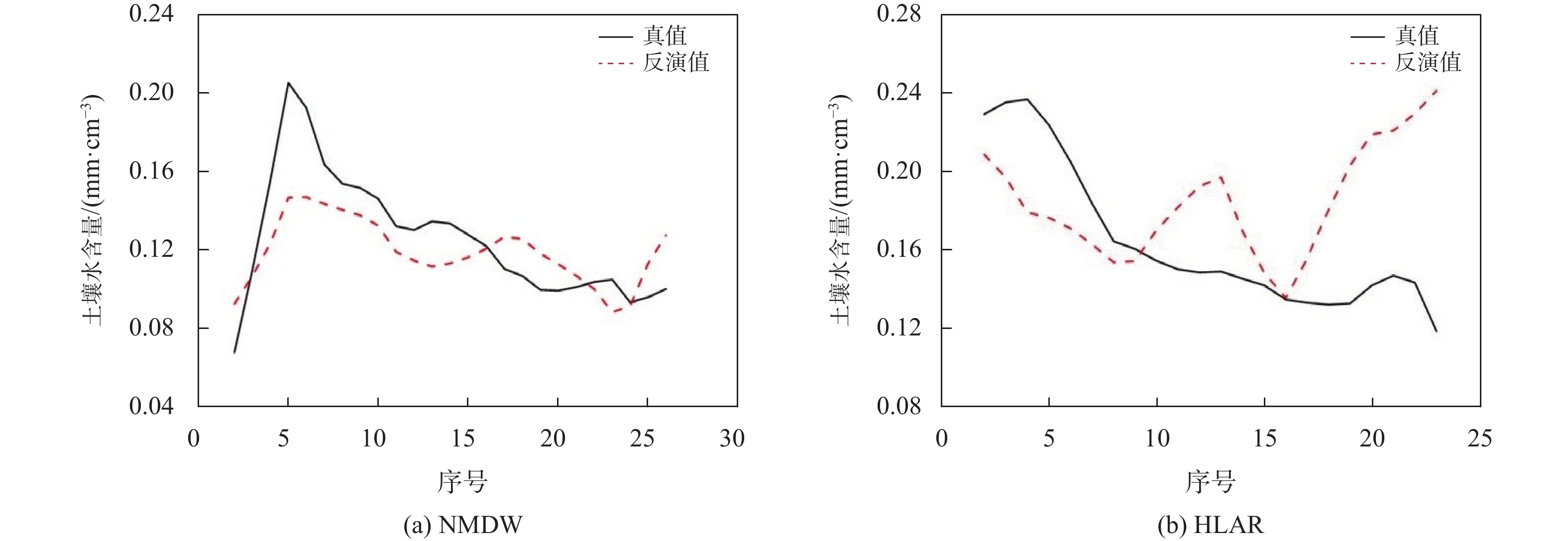
表 3 气象要素土壤水含量模型站点 常数项 湿度 日照 蒸发量 NMDW –0.012 0.207 0.008 –0.003 HLAR 0.208 0.105 –0.053 –0.015 NMAG 0.120 0.020 –0.017 –0.009 NMTK 0.142 0.086 –0.102 0.041 NMWJ 0.132 0.062 –0.032 –0.001 NMZL 0.087 0.163 –0.049 –0.002 图6为利用湿度、日照和蒸发量气象要素构建土壤水含量模型与土壤水含量真值对比分析,由图6可知该模型可以进行土壤水含量反演,但部分站点繁衍精度很低. 图6中(a)、(d)、(f)三个站点的模型土壤水含量与土壤水含量真值变化趋势基本一致,由图6(b)、(c)、(e)可知,三个站站点的反演变化趋势与实际变化趋势差距较大,反演精度较低. 且由表6可知,该方法构建模型的各实验站点误差. 由图6对比表6可知,利用湿度、日照和蒸发量构建模型具有偶然性,部分站点误差较大,不能进行土壤水含量反演.
3.2.2 利用日照、蒸发量和GNSS ZTD模型构建
因湿度与GNSS ZTD具有相关性,故作者将湿度要素去除,用GNSS ZTD代替相对平均湿度构建土壤水含量模型,并进行模型精度验证.
表4为利用日照、蒸发量和GNSS ZTD构建土壤水含量模型的常数项和各要素系数,由表4可知,该种方法构建模型,蒸发量系数较小,与3.2.1节结果相同,证明蒸发量在该模型中起约束作用. 而GNSS ZTD和日照的要素系数都较大,证明两者在该模型中为主导作用.
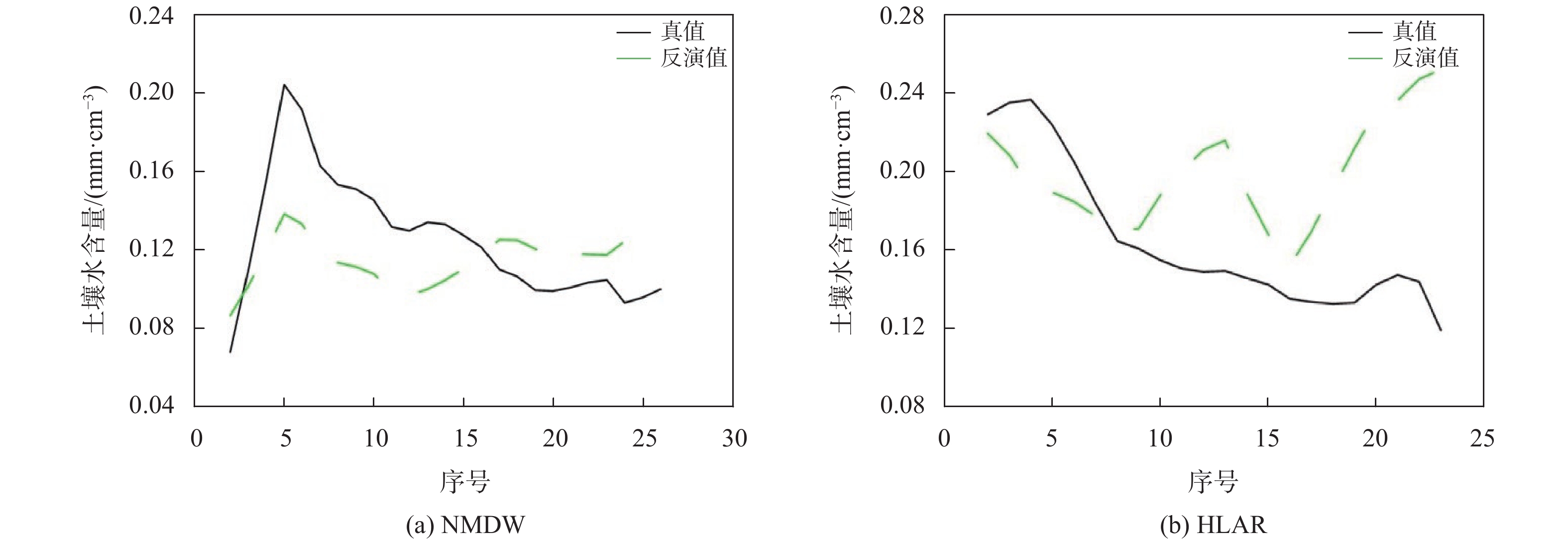
由图7可知,利用日照、蒸发量和GNSS ZTD构建模型进行土壤水含量反演效果不佳,仅(a)、(f)两站点的反演土壤水含量变化趋势与土壤水含量实际变化趋势基本相同,其他各实验站点反演土壤水含量趋势变化与土壤水含量实际趋势变化差距较大,图7结合表6分析可知,该种方法构建模型反演土壤水含误差较大,该模型不能用于土壤水含量反演工作.
表 4 日照、蒸发量和GNSS ZTD构建土壤水含量模型站点 常数项 日照 蒸发量 GNSS ZTD NMDW –0.053 –0.034 –0.013 0.101 0 HLAR 0.465 –0.073 –0.018 –0.073 0 NMAG 0.111 –0.019 –0.010 0.011 0 NMTK 0.124 –0.117 0.004 0.043 0 NMWJ 0.096 –0.040 –0.030 0.038 6 NMZL 0.154 –0.067 –0.012 0.041 8 3.2.3 融合GNSS ZTD、湿度等多项要素模型构建
由表5可知,湿度与GNSS ZTD相对于其他两种要素在模型中系数较大,所以在模型构建中该两种要素为主导作用,日照与蒸发量为约束作用.
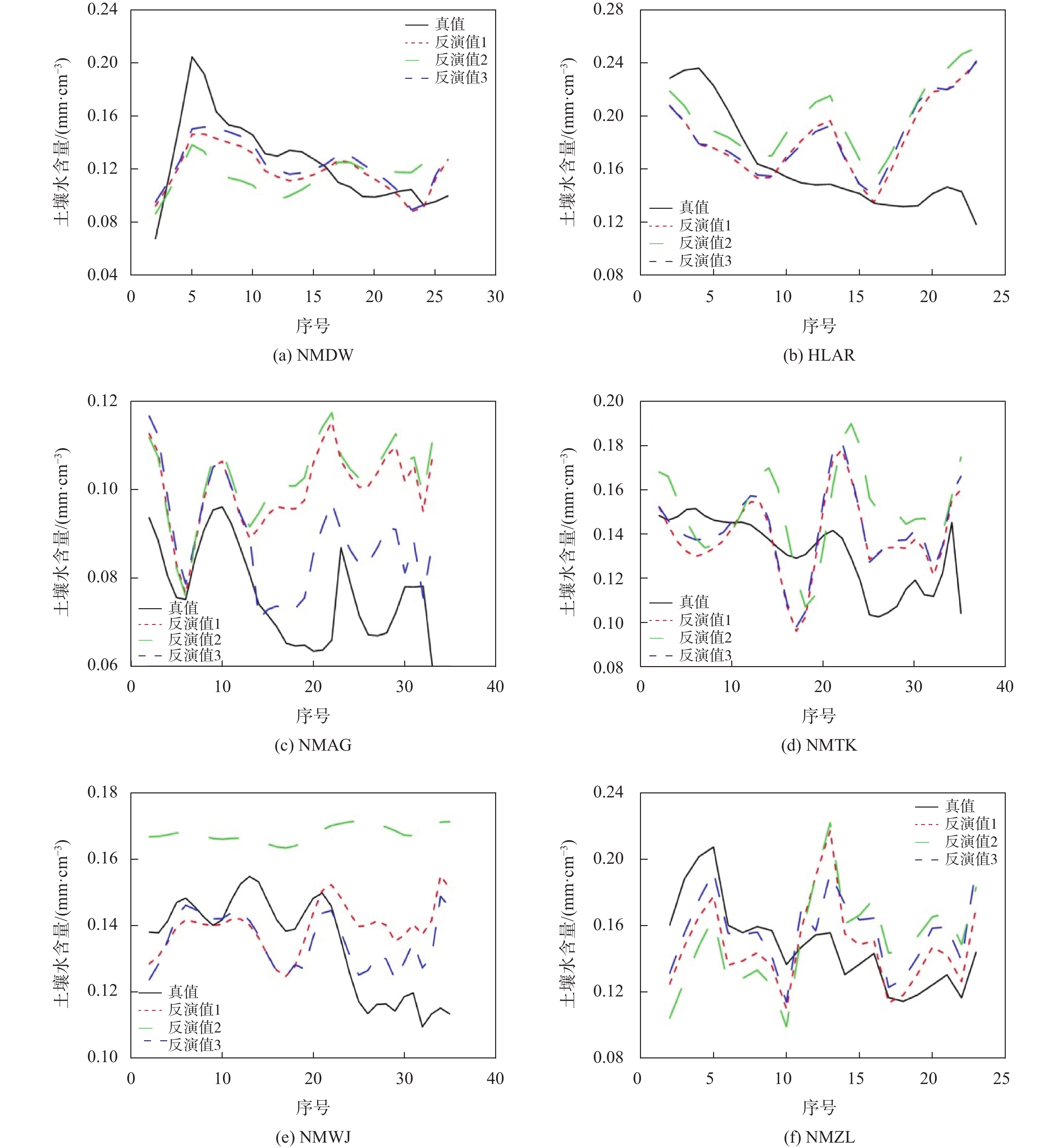
由图8可知,融合GNSS ZTD与湿度、日照和蒸 发量的土壤水含量模型,反演土壤水含量与土壤水含量真值,变化趋势基本相同,图8结合表6分析可知,该模型较于本文另两种模型反演精度有较大提高.
表 5 气象要素和GNSS ZTD土壤水含量模型站点 常数项 湿度 日照 蒸发量 GNSS ZTD/m NMDW 0.170 0.232 0.011 –0.002 –0.092 HLAR 0.698 0.202 –0.039 –0.009 –0.261 NMAG 0.312 0.051 –0.016 –0.008 –0.091 NMTK 0.360 0.129 –0.096 0.051 –0.116 NMWJ 0.344 0.103 –0.034 0.001 –0.112 NMZL 0.648 0.234 –0.049 –0.002 –0.291 表 6 土壤水含量模型误差统计m 站点 湿度、日照和蒸发量反演误差 日照、蒸发量和GNSS ZTD反演误差 湿度、日照、蒸发量和GNSS ZTD反演误差 平均偏差 RMSE 平均偏差 RMSE 平均偏差 RMSE NMDW 0.012 9 0.022 0 0.010 0 0.032 4 0.013 7 0.020 9 HLAR 0.023 0 0.051 3 0.026 3 0.056 1 0.022 3 0.050 8 NMAG 0.000 7 0.027 3 0.006 8 0.029 7 0.009 0 0.015 1 NMTK 0.013 7 0.024 4 0.014 4 0.031 4 0.013 4 0.023 3 NMWJ 0.005 2 0.017 7 0.002 0 0.370 0 0.006 5 0.013 3 NMZL 0.018 6 0.026 1 0.021 8 0.039 3 0.016 4 0.025 5 图8(c)、(e)中两站点利用该模型反演土壤水含量与土壤水含量真值变化趋势基本一致. 结合表6可知,相较于本文另两种模型,反演精度有明显提高. 而由图8(a)、(b)、(d)、(f)可知,该三种土壤水含量反演模型对比差距不大,相对于其他两种模型,融合气象要素和GNSS ZTD构建模型改正效果不显著. 表6中,融合气象要素和GNSS ZTD所构建模型相对于其他模型,均方根误差(RMSE)减小,精度提高. 其中图8(b)HLAR站点模型反演值与真值比较误差较大,反演精度较差,经表6统计可知,该站点RMSE分别为0.050 8,其精度为69.1%. 原因为该站点GNSS ZTD与土壤水含量相关性较小,但模型构建GNSS ZTD的系数较大,故引起误差较大. 而研究区域其他各站点的反演精度均超过80%,NMWJ站点反演精度达到90.1%. 本文6个实验站点的均精度为81.35%.
相对于仅用气象要素反演土壤水含量和用日照、蒸发量和GNSS ZTD的反演模土壤水含量,融合气象要素和GNSS ZTD反演土壤水含量结果与土壤水含量实际值变化更加吻合,融合气象要素和GNSS ZTD数据的模型反演数据变化与实际变化基本一致. 由表6可知,融合气象要素和GNSS ZTD的模型RMSE相对于其他两种模型RMSE均有所减小,证明融合气象要素和GNSS ZTD数据的反演模型精度更高,可靠性更好. 探究其原因为:湿度与GNSS ZTD均与土壤水含量具有相关性,在所构建模型中起主导作用,但湿度值范围为0~1(0%~100%),且未利用GNSS ZTD构建模型,所以文中3.2.1节构建模型精度受限;而湿度与土壤水含量具有较高相关性,故文中3.2.2节剔除湿度所构建模型精度不高.
4. 结论与展望
本文将气象要素和GNSS ZTD与土壤水含量进行相关性分析,建立土壤水含量反演模型,得到以下结论:
1)相对平均湿度、日照(辐射)和蒸发量均与土壤水含量有较好相关性,平均相对湿度与蒸发量存在正相关,日照和蒸发量与土壤水含量存在负相关;
2)利用气象要素和GNSS ZTD进行模型构建,湿度与GNSS ZTD在模型中占主导作用,日照和蒸发量起约束作用;
3)利用气象要素和GNSS ZTD数据同时构建土壤水反演模型精度较高,最高精度能够达到90%,研究区域的平均精度为81.35%.
本文土壤水含量数据为SMAP卫星数据,虽然精度较为可靠,但与实际数据仍有差距. 且本文研究区域为中国内蒙古地区,植被覆盖较为单一. 后期将针对利用土壤水含量实测数据进行进一步分析讨论,并对不同植被覆盖区域和不同气候类型的土壤水含量反演开展工作.
-
表 1 土壤水含量与各要素去噪前后相关性对比
站点 原数据相关性 小波分解后相关性 平均相对湿度 日照 蒸发量 GNSS ZTD 0 cm地表温度 平均相对湿度 日照 蒸发量 GNSS ZTD NMDW 0.698 –0.398 –0.511 0.143/0.063 –0.339 0.822 –0.532 –0.691 0.315 NMZL 0.590 –0.401 –0.369 0.386 –0.086/0.279 0.687 –0.515 –0.500 0.389 HLAR 0.593 –0.448 –0.575 0.113/0.163 –0.413 0.650 –0.580 –0.672 –0.192 NMTK 0.498 –0.484 –0.267 0.310 0.175/0.004 0.596 –0.681 –0.420 0.230 NMAG 0.533 –0.496 –0.492 0.329 –0.112/0.101 0.623 –0.594 –0.644 0.375 NMWJ 0.473 –0.431 –0.268 0.198 0.091/0.141 0.493 –0.464 –0.356 0.127/0.040 注:红色字体为显著性值,未标注则其显著性为0.001. 表 2 相对湿度与GNSS ZTD相关性
站点 NMAG NMDW HLAR NMTK NMWJ NMZL 相关性 0.754 –0.150 –0.303 0.562 0.335 0.361 注:表2相关性均通过显著性检验. 表 3 气象要素土壤水含量模型
站点 常数项 湿度 日照 蒸发量 NMDW –0.012 0.207 0.008 –0.003 HLAR 0.208 0.105 –0.053 –0.015 NMAG 0.120 0.020 –0.017 –0.009 NMTK 0.142 0.086 –0.102 0.041 NMWJ 0.132 0.062 –0.032 –0.001 NMZL 0.087 0.163 –0.049 –0.002 表 4 日照、蒸发量和GNSS ZTD构建土壤水含量模型
站点 常数项 日照 蒸发量 GNSS ZTD NMDW –0.053 –0.034 –0.013 0.101 0 HLAR 0.465 –0.073 –0.018 –0.073 0 NMAG 0.111 –0.019 –0.010 0.011 0 NMTK 0.124 –0.117 0.004 0.043 0 NMWJ 0.096 –0.040 –0.030 0.038 6 NMZL 0.154 –0.067 –0.012 0.041 8 表 5 气象要素和GNSS ZTD土壤水含量模型
站点 常数项 湿度 日照 蒸发量 GNSS ZTD/m NMDW 0.170 0.232 0.011 –0.002 –0.092 HLAR 0.698 0.202 –0.039 –0.009 –0.261 NMAG 0.312 0.051 –0.016 –0.008 –0.091 NMTK 0.360 0.129 –0.096 0.051 –0.116 NMWJ 0.344 0.103 –0.034 0.001 –0.112 NMZL 0.648 0.234 –0.049 –0.002 –0.291 表 6 土壤水含量模型误差统计
m 站点 湿度、日照和蒸发量反演误差 日照、蒸发量和GNSS ZTD反演误差 湿度、日照、蒸发量和GNSS ZTD反演误差 平均偏差 RMSE 平均偏差 RMSE 平均偏差 RMSE NMDW 0.012 9 0.022 0 0.010 0 0.032 4 0.013 7 0.020 9 HLAR 0.023 0 0.051 3 0.026 3 0.056 1 0.022 3 0.050 8 NMAG 0.000 7 0.027 3 0.006 8 0.029 7 0.009 0 0.015 1 NMTK 0.013 7 0.024 4 0.014 4 0.031 4 0.013 4 0.023 3 NMWJ 0.005 2 0.017 7 0.002 0 0.370 0 0.006 5 0.013 3 NMZL 0.018 6 0.026 1 0.021 8 0.039 3 0.016 4 0.025 5 -
[1] LARSON K M, BRAUN J J, SMALL E E, et al. GPS multipath and its relation to near-surface soil moisture content[J]. IEEE journal of selected topics in applied earth observations and remote sensing, 2010, 3(1): 91-99. DOI: 10.1109/JSTARS.2009.2033612
[2] BOWERS S A, HUNKS R J. Reflection of radiant energy from soils[J/OL]. [2021-08-30]. Soil science, 1965, 100 (2): 130-138. https://journals.lww.com/soilsci/Citation/1965/08000/REFLECTION_OF_RADIANT_ENERGY_FROM_SOILS.9.aspx
[3] SCHMUGGE T, GLOERSEN P, WILHEIT T T, er al. Remote sensing of soil moisture with microwave radiometers[J]. Journal of geophysical research, 1974, 79(2): 317-323. DOI: 10.1029/JB079i002p00317
[4] 张焕武, 何林轩. 淄博地区SMAP卫星干扰原因分析[J]. 中国无线电, 2017(12): 64-65. DOI: 10.3969/j.issn.1672-7797.2017.12.038 [5] 周延. 对排查SMOS卫星干扰的思考[J]. 中国无线电, 2018(3): 66 DOI: 10.3969/j.issn.1672-7797.2018.03.043 [6] MLADENOVA I, LAKSHMI V, JACKSON T J, et al. Validation of AMSR-E soil moisture using L-band airborne radiometer data from National Airborne Field Experiment 2006[J]. Remote sensing of environment, 2011, 115(8): 2096-2103. DOI: 10.1016/j.rse.2011.04.011
[7] 罗志才, 李琼, 钟波. 利用GRACE时变重力场反演黑河流域水储量变化[J]. 测绘学报, 2012, 41(5): 676-681. [8] 张为民, 王勇, 张赤军. 土壤浸湿对重力观测影响的初步分析[J]. 测绘学报, 2001, 30(2): 108-111. DOI: 10.3321/j.issn:1001-1595.2001.02.003 [9] 李明星, 马柱国, 杜继稳. 区域土壤湿度模拟检验和趋势分析-以陕西省为例[J]. 中国科学 (地球科学), 2010(3): 363-379. [10] FASINMIRIN J T, OLUFAYO A A, OGUNTUNDE P G. Calibration and validation of a soil water simulation simulation model for field grown Amaranthus cruentus[J]. International journal of plant produbtion, 2008, 2(3): 269-278.
[11] NAKHAEI M, ŠIMŮNEK J. Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code[J]. Journal of hydrology and hydromechanics, 2014, 62(1): 7-15. DOI: 10.2478/johh-2014-0008
[12] RANA G, KATERJI N. Measurement and estimation of actual evapotranspiration in the field under mediterranean climate: a review[J]. European journal of agronomy, 2000, 13(2-3): 125-153. DOI: 10.1016/S1161-0301(00)00070-8
[13] 王雷, 刘辉志, BERNHOFER C. 土壤水分条件对内蒙古典型草原水汽和二氧化碳通量的影响研究[J]. 大气科学, 2017, 41(1): 167-177. [14] 王轩, 娄泽生. 基于小波变换的GNSS ZTD与土壤水含量相关性初探[J]. 全球定位系统, 2019, 44(4): 77-81. [15] LA PIERRE K J, YUAN S H, CHANG C C, et al. Explaining temporal variation in above-ground productivity in a mesic grassland: the role of climate and flowering[J]. Journal of ecology, 2011, 99(5): 1 250-1262. DOI: 10.1111/j.1365-2745.2011.01844.x
[16] RUPPERT J C, HARMONEY K, HENKIN Z, et al. Quantifying drylands’drought resistance and recovery: the importance of drought intensity, dominant life history and grazing regime[J]. Global change biolog, 2015, 21(3): 1258-1270. DOI: 10.1111/gcb.12777
[17] 张德丰. MATLAB小波分析 [M]. 北京: 机械工业出版社, 2011. [18] 王勇, 任栋, 刘严萍, 等. 基于小波变换与回归分析的融合GNSS水汽、风速和PM10要素的PM2.5浓度模型[J]. 系统工程理论与实践, 2020, 40(3): 761-770. DOI: 10.12011/1000-6788-2018-2048-10 -
期刊类型引用(1)
1. 王慧,李靖瑄,刘小妮,沈丽娟,吴晓文,鲁素芬. 基于气象因子的土壤含水量模拟研究. 水利规划与设计. 2022(11): 37-45 .  百度学术
百度学术
其他类型引用(0)




 下载:
下载: