A method for designing the loop parameters of digital PLL based on equivalent signal model
-
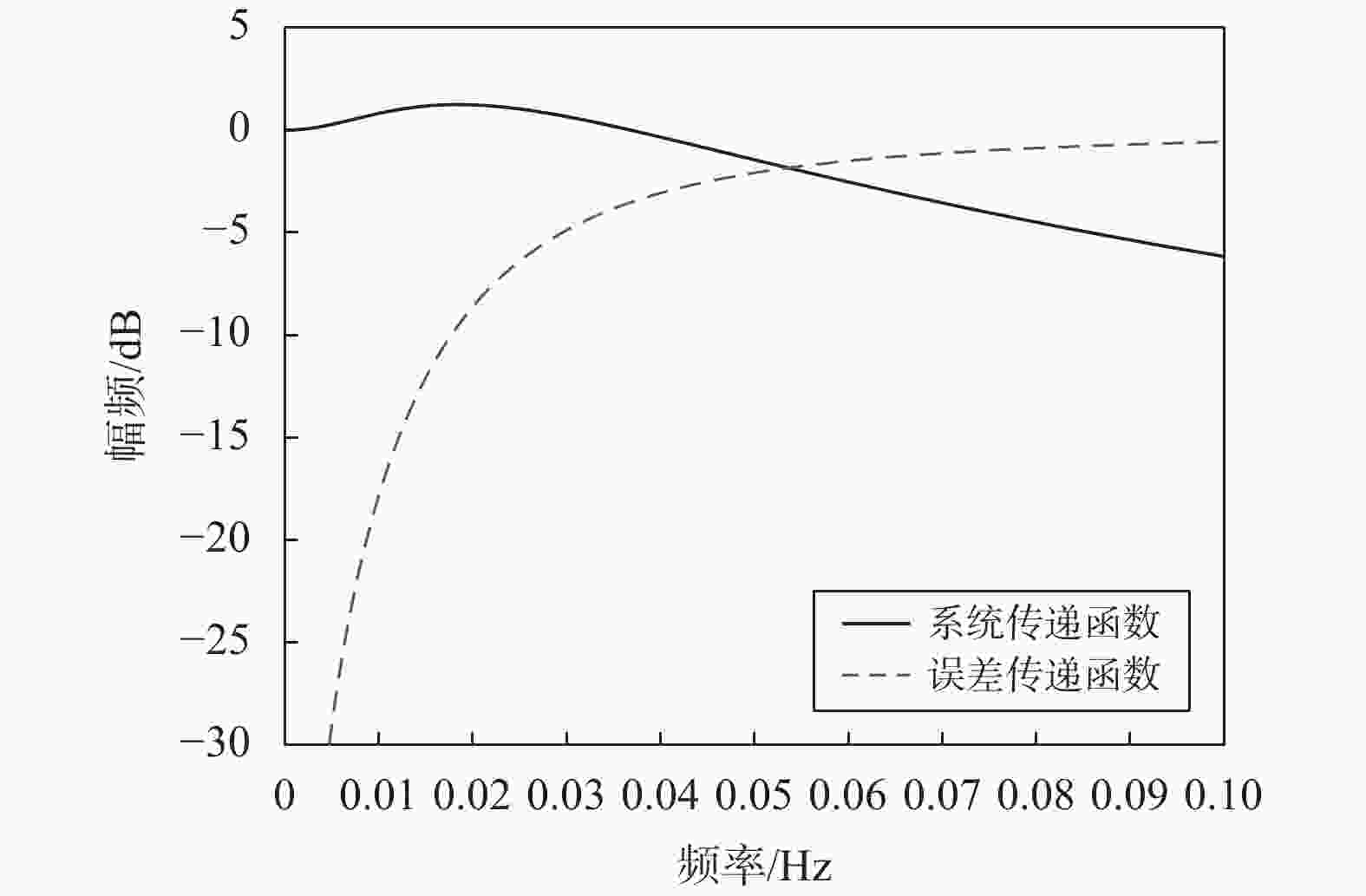
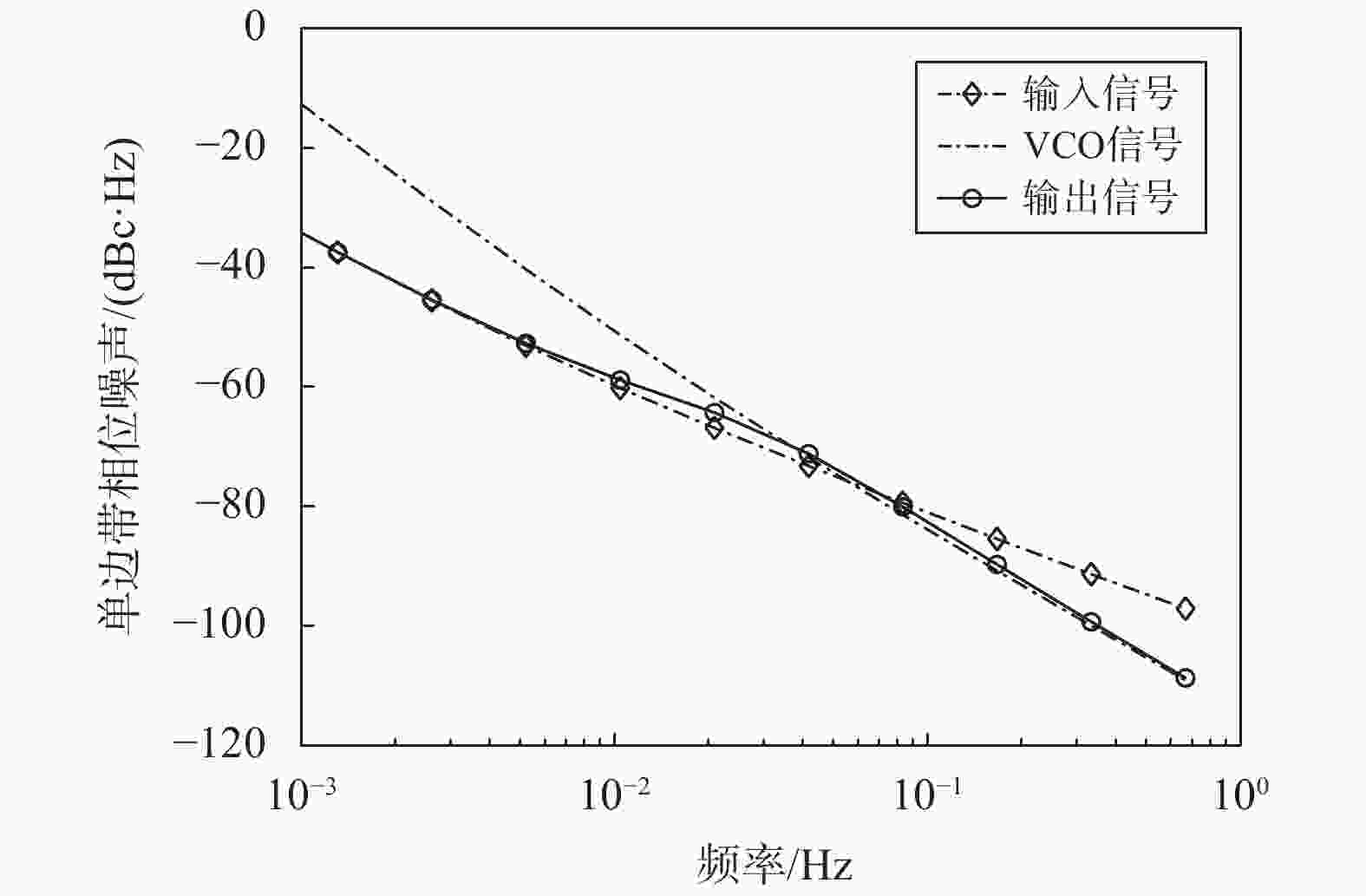
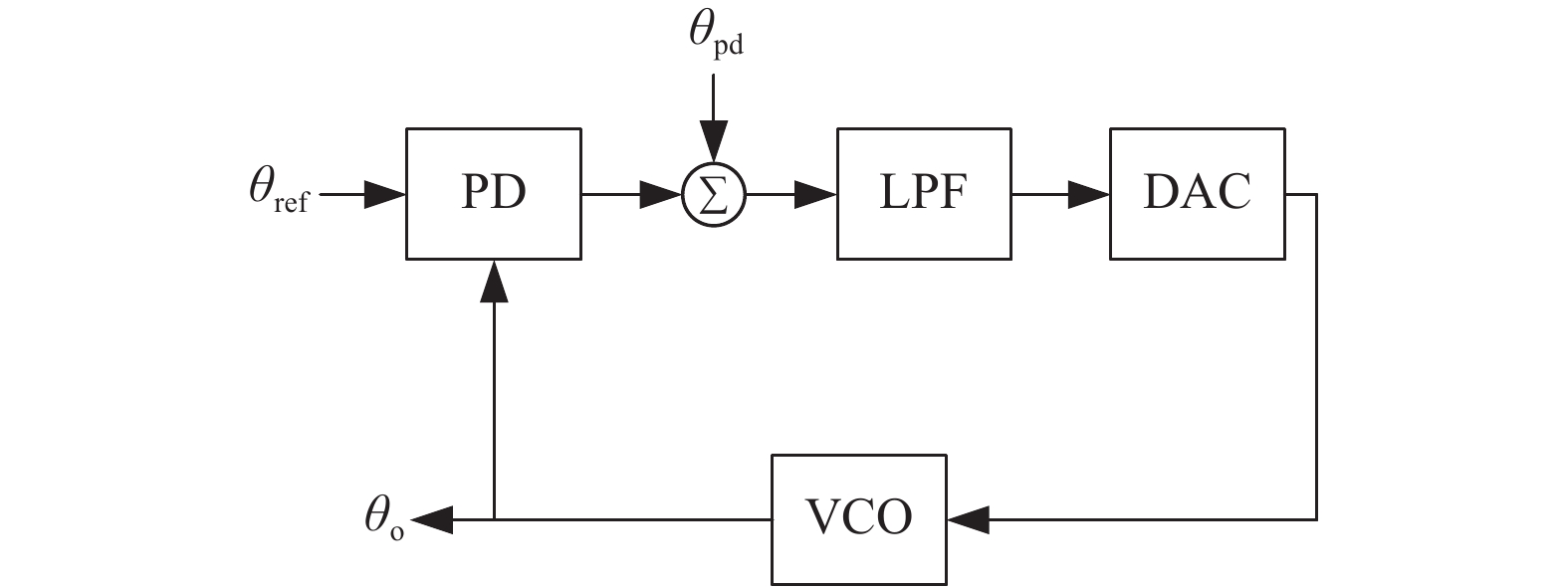
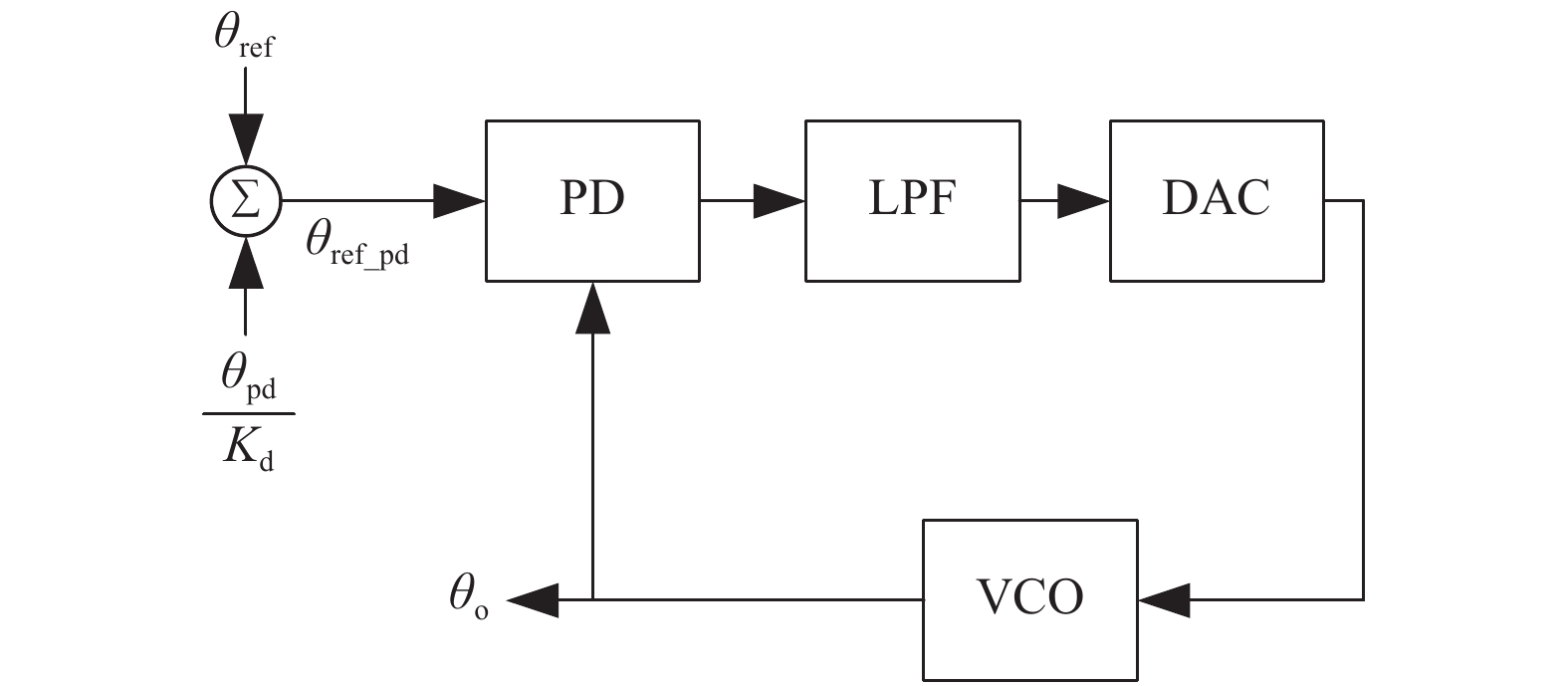
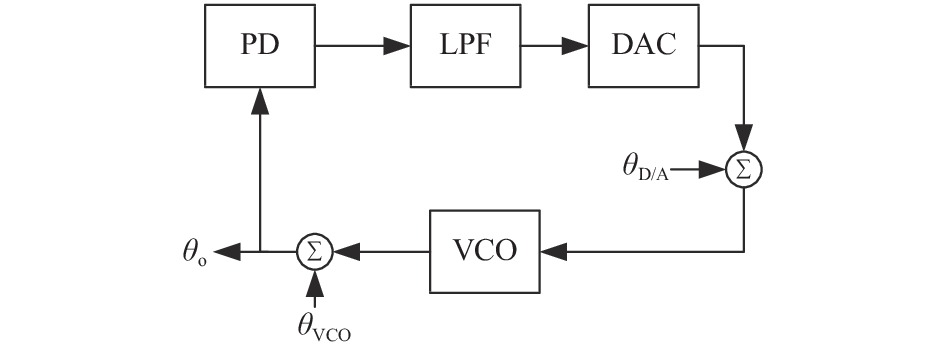
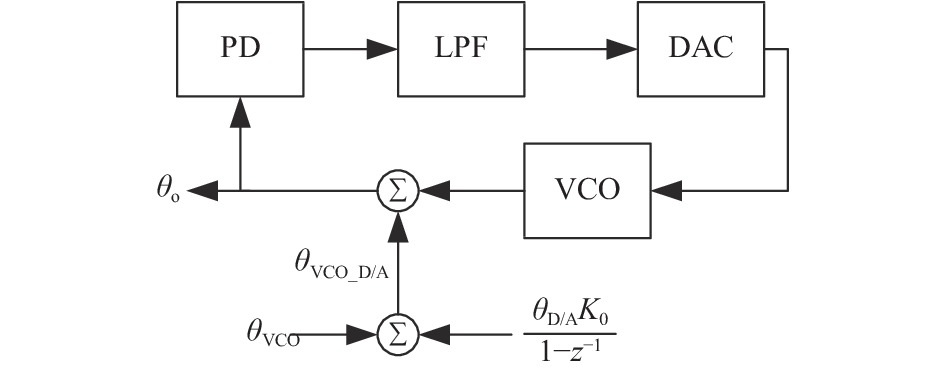
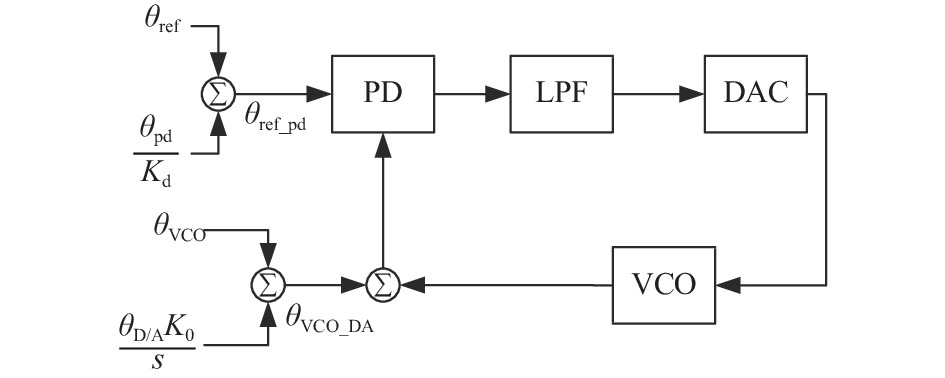
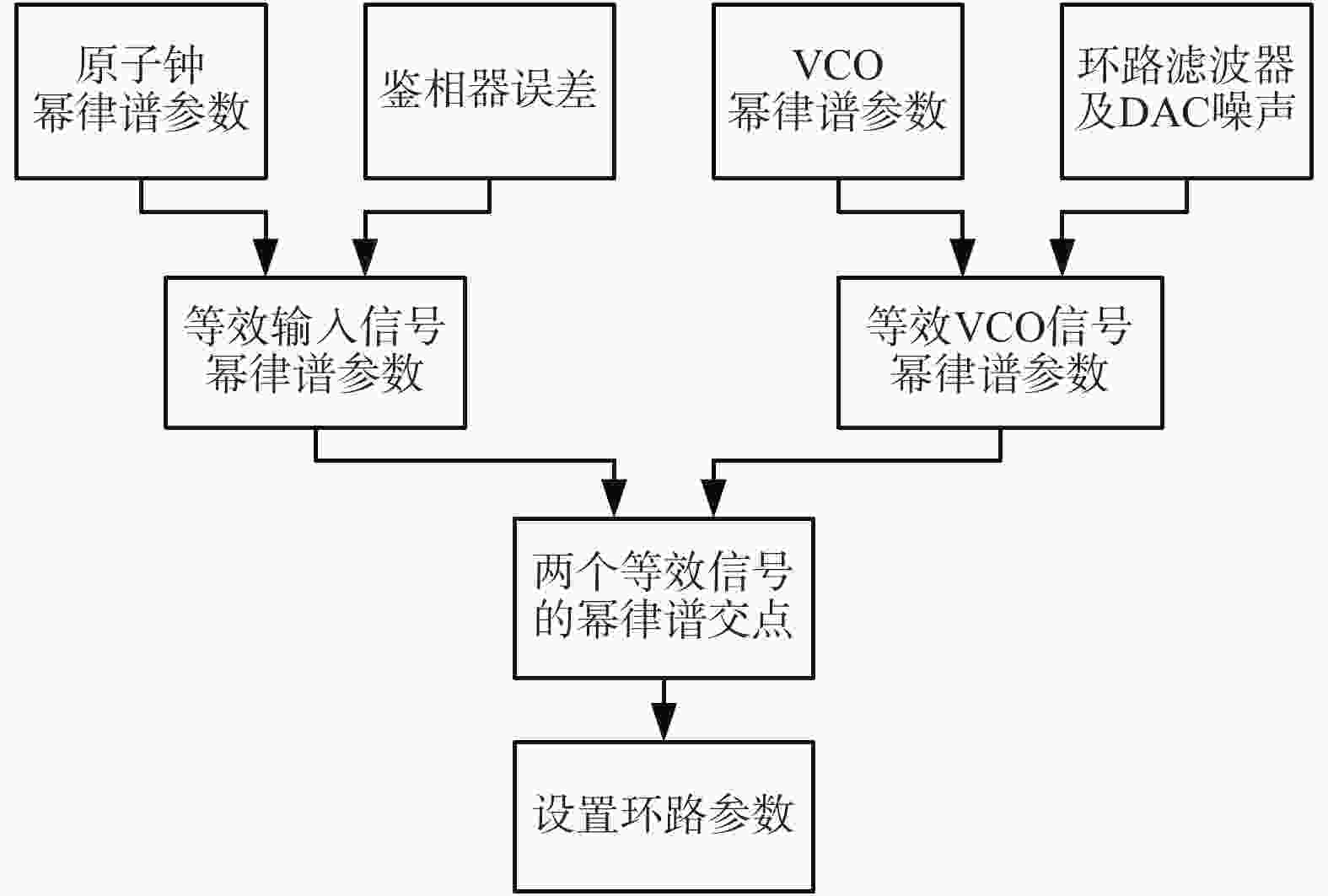
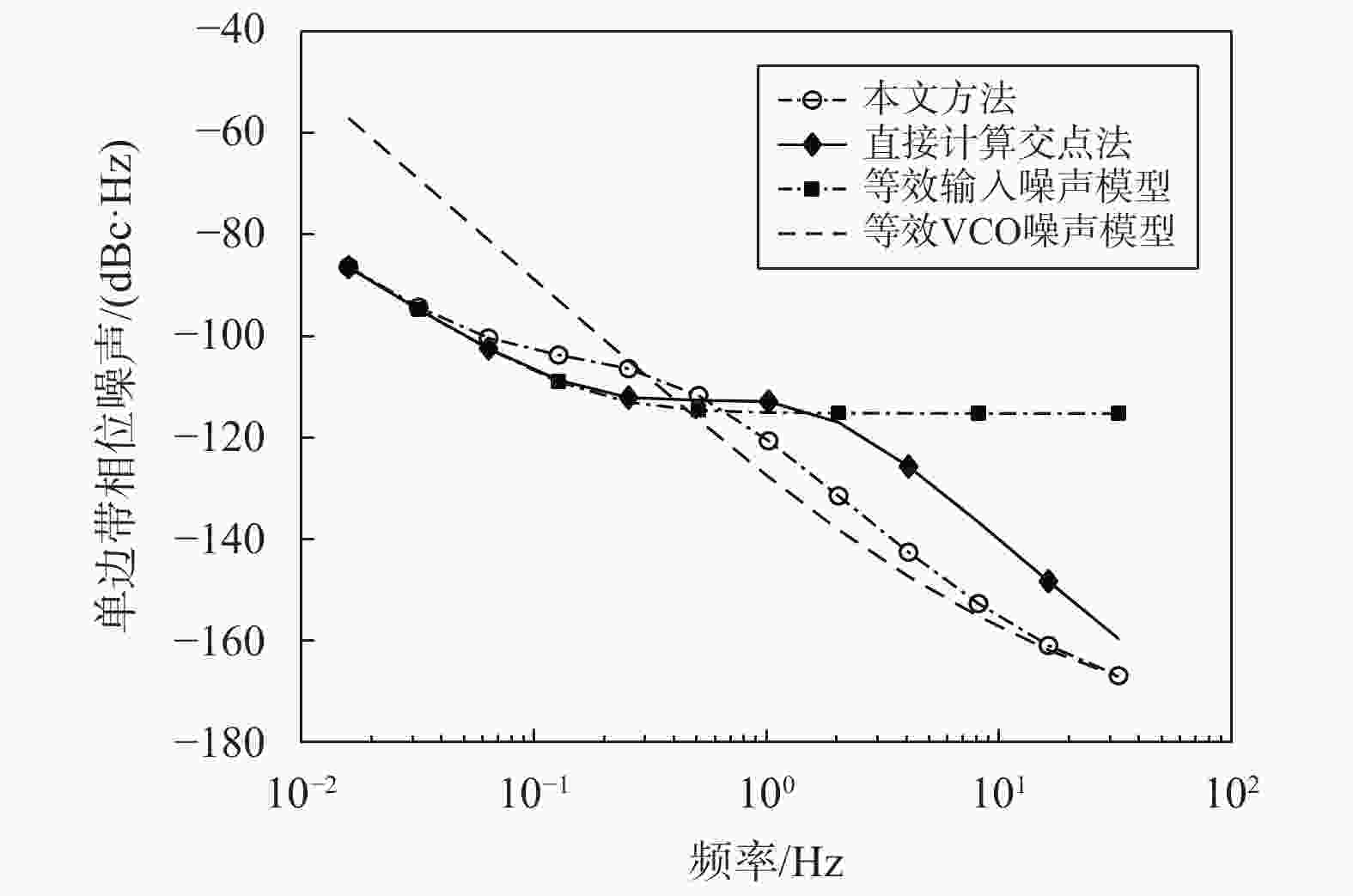
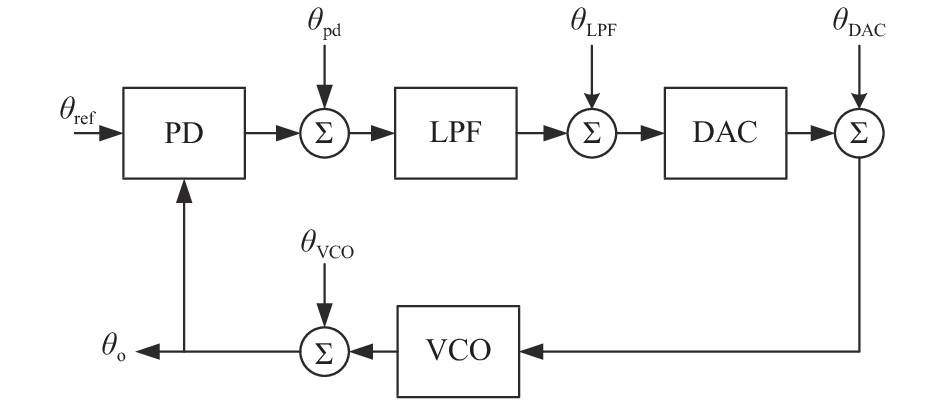
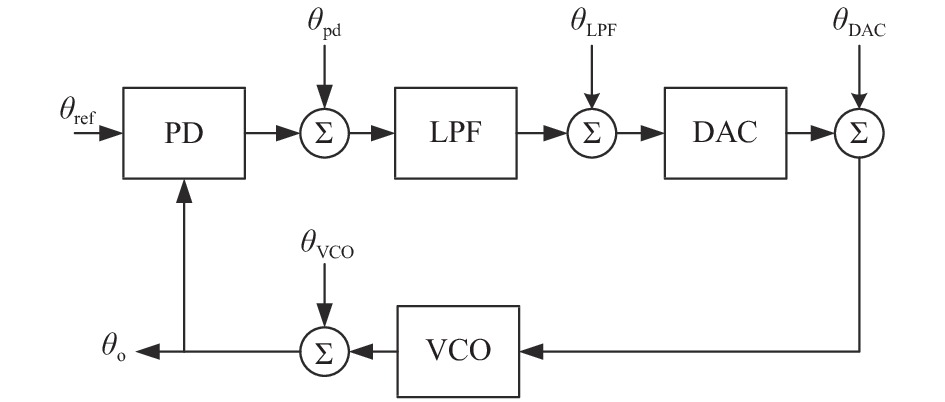
摘要: 理想情况下,数字锁相环(DPLL)的环路参数可以通过直接计算输入原子钟与压控振荡器(VCO)的相位噪声功率谱交点来确定. 但该方法不能考虑到锁相环(PLL)其他模块的噪声,这会导致输出性能恶化. 针对这一问题,文中从PLL模型出发,基于PLL环路传递函数和幂律谱模型,提出PLL模块噪声的等效方法. 该方法将PLL各模块噪声分别等效到输入和VCO的相位噪声上,使得PLL的噪声传递模型只含有等效输入噪声和等效VCO噪声. 然后可以直接计算两者相位噪声交点并设置合理的环路参数. 通过该方法确定的环路参数可以充分结合输入原子钟信号和VCO信号的相位噪声和频率稳定度特性,弥补了直接计算交点法不能考虑模块噪声的缺点. 实验表明:文中方法所选择的环路参数能使得输出信号具备良好的稳定度,可以为应用于净化原子钟信号的数字锁相装置环路参数的确定提供理论指导.Abstract: Ideally, the loop parameters of an digital phase-locked loop (DPLL) is determined by the intersection of the phase noise of the input signal and the voltage-controlled oscillator (VCO). However, the basic module of the phase-locked loop (PLL) will introduce noise into the PLL system, thereby affecting the PLL performance. The method of directly calculating the intersection point of the two cannot take into account the influence of module noise. With the theory of the power-law spectrum model, this paper uses the PLL transfer model to superimpose the noise of the basic module of the PLL on the signal model of the atomic clock and the VCO. After establishing new signal models, it can conveniently and quickly determine the optimal loop parameters of the PLL. The simulation shows that the loop parameters selected by this method can make the output signal have good frequency stability, which can provide theoretical guidance for the selection of the loop parameters of the digital phase-locked device used to purify the atomic clock signal.
-
表 1 实验参数
参数 值 系统采样率 100 Hz 鉴相误差 U(−3 ps, 3 ps) ${K_d}$ 1 ${K_0}$ 1 DAC位数 24 VCO压控牵引范围 10−7 -
[1] YU M Y, WANG Y, WAN J Y, et al. Low phase noise microwave frequency synthesizer for cold atom clock[J]. AIP advances, 2019, 9(4): 045223. DOI: 10.1063/1.5093165 [2] SURESH B, VISVANATHAN V, KRISHNAN R S, et al. Application of alpha power law models to PLL design methodology[C]//The 18th International Conference on VLSI Design held jointly with 4th International Conference on Embedded Systems Design, 2005. DOI: 10.1109/ICVD.2005.54 [3] 张杰, 马冠一. GNSS接收机锁相环最佳环路带宽的选取[J]. 电讯技术, 2015, 55(8): 890-894. DOI: 10.3969/j.issn.1001-893x.2015.08.011 [4] 孙家星, 孙越强, 杜起飞. 锁相环频率合成器最优环路带宽的选取[J]. 固体电子学研究与进展, 2016, 36(6): 457-459, 500. [5] CURRAN J T, LACHAPELLE G, MURPHY C C. Digital GNSS PLL design conditioned on thermal and oscillator phase noise[J]. IEEE transactions on aerospace and electronic systems, 2012, 48(1): 180-196. DOI: 10.1109/TAES. 2012.6129629 [6] STEVANOVIC S, PERVAN B. A GPS phase-locked loop performance metric based on the phase discriminator output[J]. Sensors, 2018, 18(1): 296. DOI: 10.3390/s18010296 [7] WU Y W, GONG H, ZHU X W, et al. A clock steering method: using a third-order type 3 DPLL equivalent to a Kalman filter with a delay[J]. Metrologia, 2015, 52(6): 864-877. DOI: 10.1088/0026-1394/52/6/864 [8] WU Y W, GONG H, ZHU X W, et al. A DPLL method applied to clock steering[J]. IEEE transactions on instrumentation and measurement, 2016, 65(6): 1331-1342. DOI: 10.1109/TIM.2016.2526699 [9] KASDIN N J. Discrete simulation of colored noise and stochastic processes and 1/f power law noise generation[J]. Proceedings of the IEEE, 1995, 83(5): 802-827. DOI: 10.1109/5.381848 [10] D'APUZZO M, D'ARCO M, MORIELLO R S L. A composite-power-law noise generator[C]//IEEE Instrumentation and Measurement Technology Conference, 2008. DOI: 10.1109/IMTC.2008.4547146 [11] CHORTI A, BROOKES M. A spectral model for RF oscillators with power-law phase noise[J]. IEEE transactions on circuits and systems I: regular papers, 2006, 53(9): 1989-1999. DOI: 10.1109/TCSI.2006.881182 [12] 王敏格. 全数字锁相环的研究与设计[D]. 北京: 北京交通大学, 2018. [13] 张攀. 高频CMOS数字锁相环关键技术研究[D]. 西安: 西安电子科技大学, 2018. [14] 闫菲菲, 马红皎, 何在民, 等. 基于FPGA和TDC芯片的高精度时间间隔计数器研制[J]. 时间频率学报, 2019, 42(1): 33-42. [15] 邓小莺. 全数字锁相环抖动和相位噪声的研究[D]. 南京: 东南大学, 2012. [16] 宋复成, 顾明亮, 杨增汪. 用DAC0832芯片实现32位D/A的高分辨率[J]. 微计算机信息, 2007, 23(20): 293-294. DOI: 10.3969/j.issn.1008-0570.2007.20.119 -




 下载:
下载: