Application analysis of PPP-RTK technology based on the BeiDou Navigation Satellite System in UAV power inspection
-
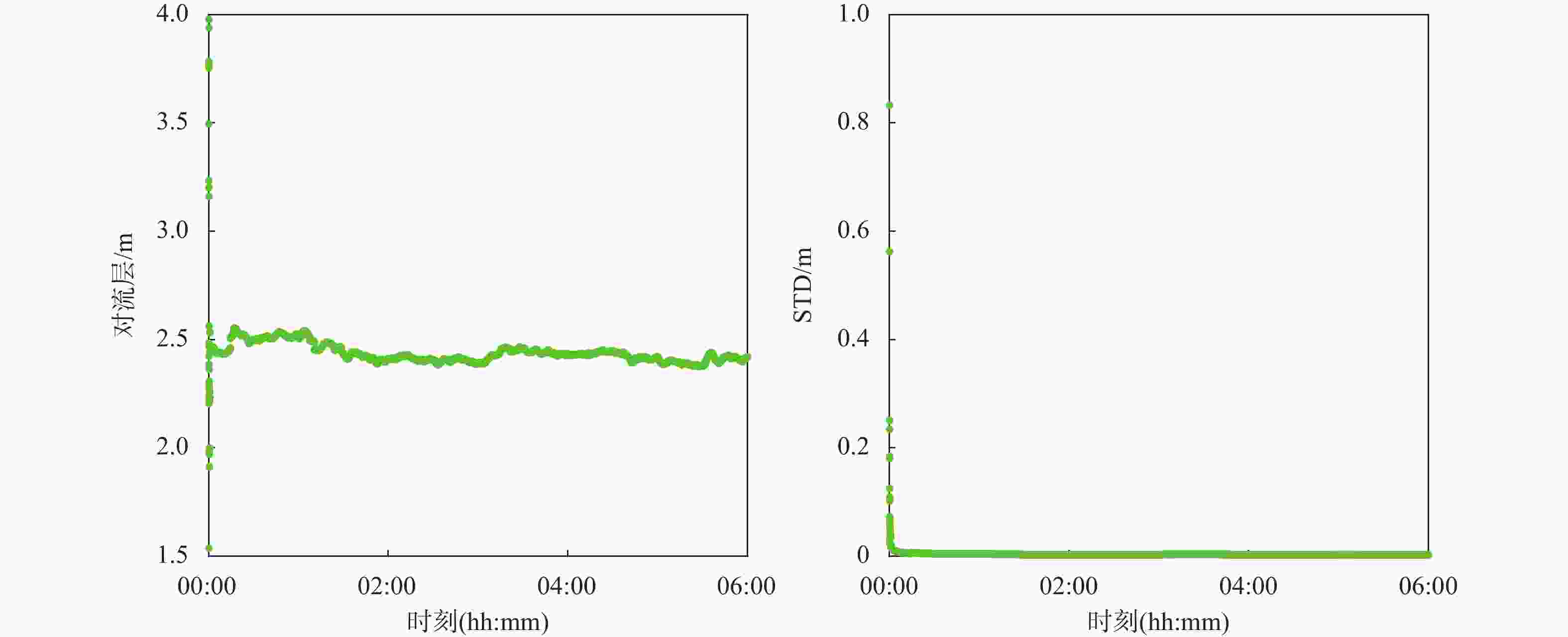
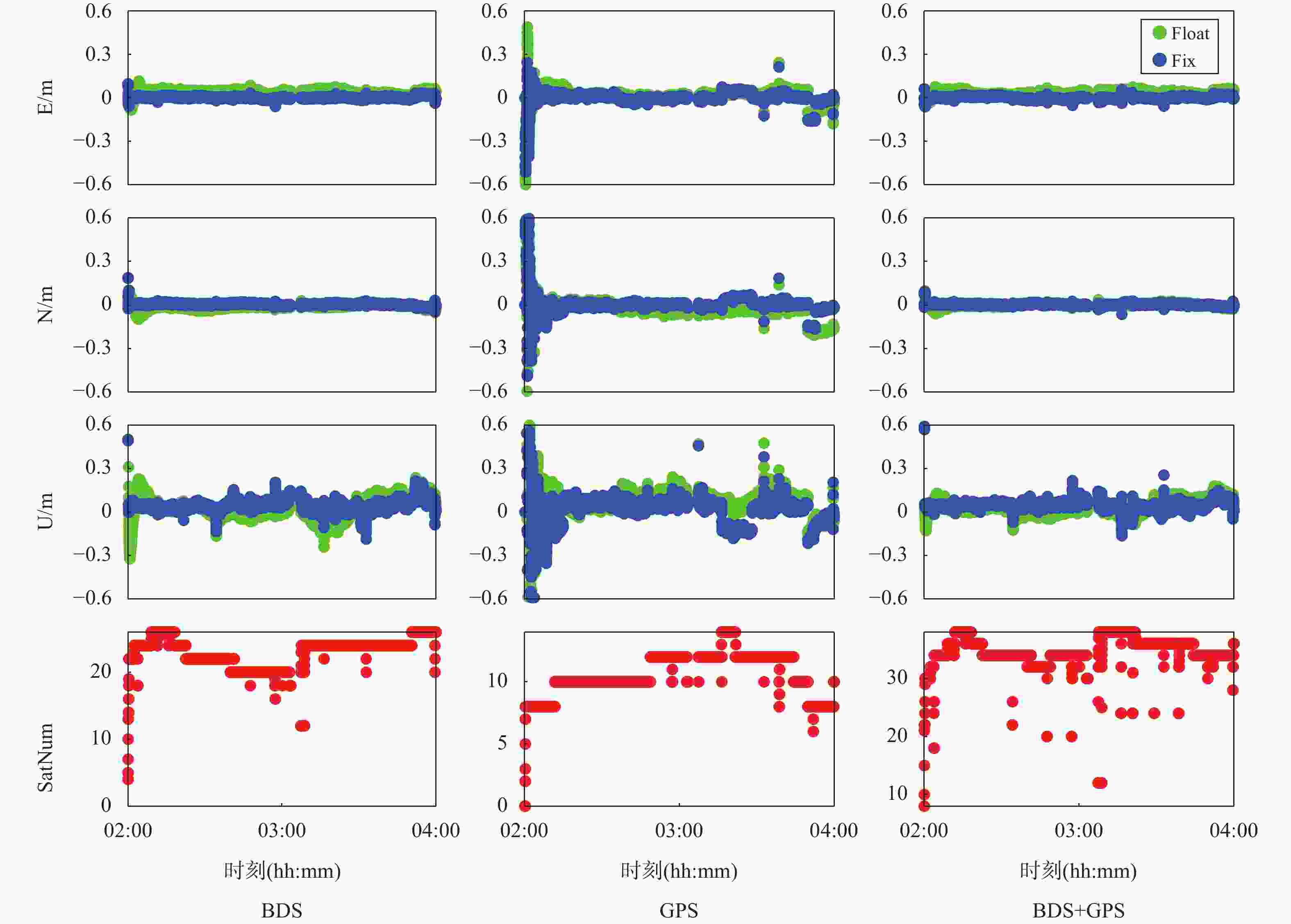
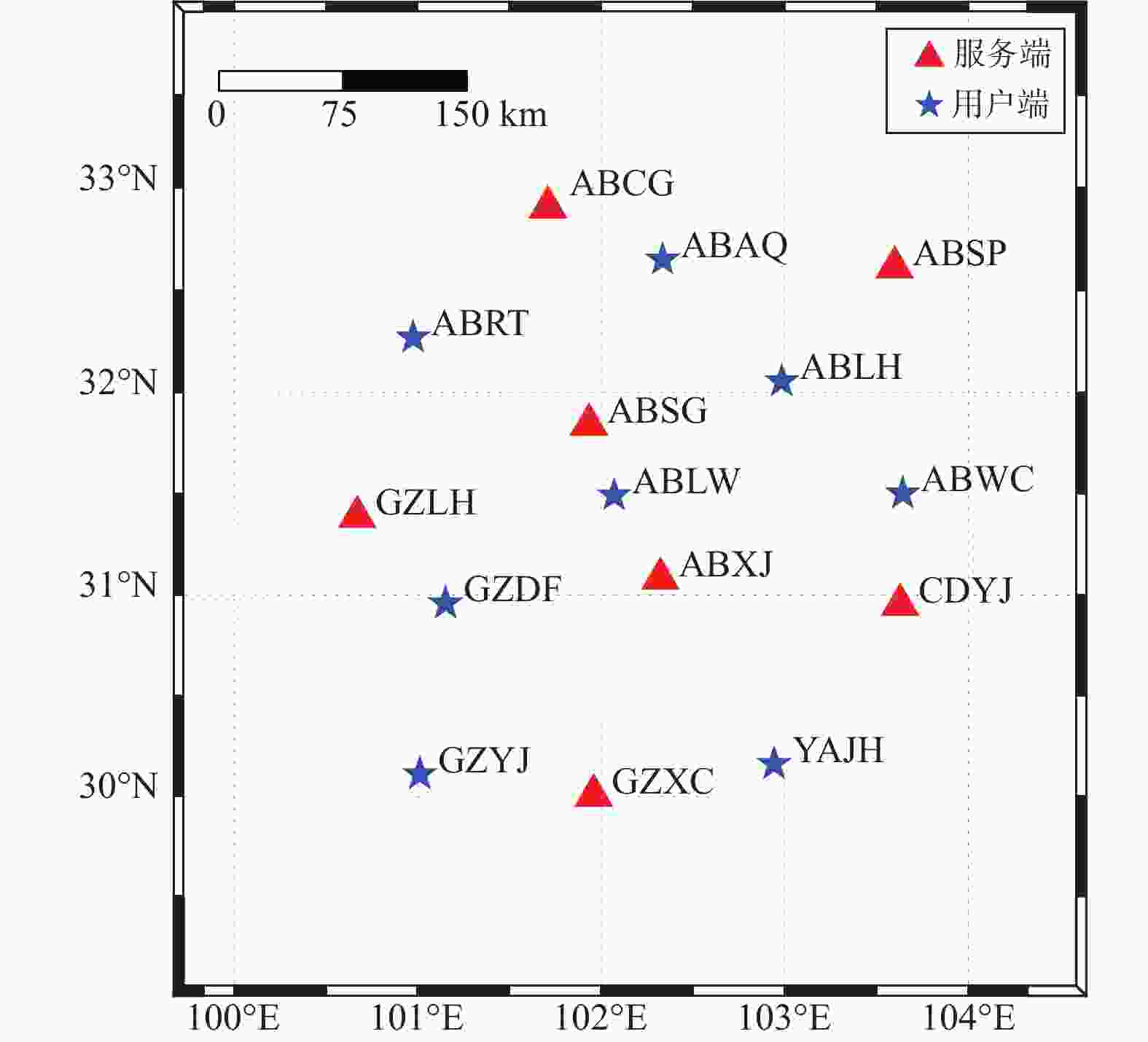
摘要: 为解决无公网地区或地形条件复杂地区进行无人机电力巡检得不到高精度定位服务的问题,本文提出使用基于北斗卫星导航系统(BeiDou Navigation Satellite System, BDS)的精密单点定位-实时动态定位(precise point positioning-real-time kinematic, PPP-RTK)技术,为无人机电力巡检提供高精度定位服务. 文中使用电力北斗精准位置服务网四川省内电力北斗基准站的数据进行了PPP-RTK服务端产品的计算和用户端的仿动态定位试验. 试验结果表明:在使用基于BDS的PPP-RTK服务条件下,用户端使用BDS或BDS+GPS进行PPP-RTK模糊度固定解模式时,在1 min内就可以实现收敛,收敛后水平方向的均方根 (root mean square, RMS) 值小于5 cm,高程方向的RMS小于8 cm,该试验结果可以为构建电力北斗PPP-RTK服务及其在无人机巡检中的应用提供设计参考依据.
-
关键词:
- 北斗卫星导航系统(BDS) /
- 精密单点定位-实时动态定位(PPP-RTK) /
- 无人机电力巡检 /
- 电力行业
Abstract: In order to solve the problem that high-precision positioning service is not available for UAV power inspection in areas with no public network or complex terrain conditions, this paper proposes to use precise point positioning-real-time kinematic (PPP-RTK) technology based on BeiDou Navigation Satellite System (BDS) to provide high-precision positioning service for UAV power inspection. Using data from the electric power BeiDou precise positioning service network in Sichuan province to calculate the PPP-RTK server-side product and conduct user-side simulated dynamic positioning experiments. The experimental results show that under the conditions of using BDS-based PPP-RTK services, when the user-side adopts BDS or BDS+GPS for PPP-RTK integer ambiguity resolution, convergence can be achieved within 1 minute. After convergence, the horizontal direction root mean square (RMS) is less than 5 cm, and the vertical direction RMS is less than 8 cm. The experimental results can provide design reference for the construction of power BeiDou PPP-RTK service and its application in UAV inspection. -
表 1 非差非组合PPP-RTK各类参数可估形式
参数 可估形式 $ {\tilde{\rm{d}}}t^{s}\left(i\right) $ $ {\mathrm{d}t}^{s}\left(i\right)-{\mathrm{d}t}_{1}\left(i\right)+{d}_{\mathrm{I}\mathrm{F}}^{s}-{{d}_{1,\mathrm{I}\mathrm{F}}-g}_{1}^{s}\left(i\right)\cdot {\tau }_{1}\left(i\right) $ $ \tilde{{d}}_{j > 2}^{s} $ $ {d}_{j}^{s}-{d}_{\mathrm{I}\mathrm{F}}^{s}-{\mu }_{j}{d}_{\mathrm{G}\mathrm{F}}^{s}-{d}_{1,j}+{d}_{1,\mathrm{I}\mathrm{F}}+{\mu }_{j}{d}_{1,\mathrm{G}\mathrm{F}} $ $ {\tilde{\delta }}_{j}^{s} $ $ {\delta }_{j}^{s}-{d}_{\mathrm{I}\mathrm{F}}^{s}+{\mu }_{j}{d}_{\mathrm{G}\mathrm{F}}^{s}-{\delta }_{1,j}+{d}_{1,\mathrm{I}\mathrm{F}}-{\mu }_{j}{d}_{1,\mathrm{G}\mathrm{F}}{-\lambda }_{j}{N}_{1,j}^{s} $ $ {\tilde{N}}_{r\ne 1,j}^{s\ne q} $ $ {N}_{1r,j}^{s}-{N}_{1r,j}^{q} $ $ {\tilde{\tau }}_{r\ne 1}\left(i\right) $ $ {\tilde{\tau }}_{1r}\left(i\right) $ $ {\tilde{\rm{d}}t}_{r\ne 1}\left(i\right) $ $ {d}_{1r}\left(i\right)+{d}_{1r,\mathrm{I}\mathrm{F}} $ $ {\tilde{d}}_{r\ne 1,j > 2} $ $ {d}_{1r,j}\left(i\right)-{d}_{1r,\mathrm{I}\mathrm{F}}-{\mu }_{j}{d}_{1r,\mathrm{G}\mathrm{F}} $ $ {\tilde{\delta }}_{r\ne 1,j} $ $ {\delta }_{1r,j}-{d}_{1r,\mathrm{I}\mathrm{F}}+{\mu }_{j}{d}_{1r,\mathrm{G}\mathrm{F}}{+\lambda }_{j}{N}_{1r,j}^{q} $ $ {\tilde{I}}_{r,j}^{s}\left(i\right) $ $ {I}_{r,j}^{s}\left(i\right) $+ $ {d}_{r,\mathrm{G}\mathrm{F}}-{d}_{\mathrm{G}\mathrm{F}}^{s} $ 表 2 BDS/GPS/GPS+BDS 定位平均收敛时间与RMS
系统 解算
模式RMS_
E/cmRMS_
N/cmRMS_
U/cm收敛时间/
minBDS 浮点解 4.0 1.5 8.2 15.7 固定解 0.8 0.7 6.3 0.5 GPS 浮点解 5.1 7.0 13.6 9.9 固定解 3.3 3.5 12.5 4.7 BDS+GPS 浮点解 4.2 1.1 5.7 15.1 固定解 0.9 0.7 6.1 0.2 -
[1] 李静, 龙强, 臧志斌, 等. 北斗卫星导航系统在电力行业的应用研究[J]. 电力信息与通信技术, 2022, 20(10): 87-97. [2] 李征航, 黄劲松. GPS 测量与数据处理[M]. 武汉: 武汉大学出版社, 2005. [3] 黄丁发, 周乐韬, 李成钢. GPS 增强参考站网络理论[M]. 北京: 科学出版社, 2011. [4] WABBENA G, SCHMITZ M, BAGGE A. PPP-RTK: precise point positioning using state-space representation in RTK networks[C]//The 18th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS 2005). 2005: 2584-2594. [5] TEUNISSEN P J G, ODIJK D, ZHANG B C. PPP-RTK: results of CORS network-based PPP with integer ambiguity resolution[J]. Journal of aeronautics, astronautics and aviation, A, 2010, 42(4): 223-229. [6] 张宝成, ODIJK D. 一种能实现单频PPP-RTK的GNSS局域参考网数据处理算法[J]. 地球物理学报, 2015, 58(7): 2306-2319. [7] ZHANG B C, CHEN Y C, YUAN Y B. PPP-RTK based on undifferenced and uncombined observations: theoretical and practical aspects[J]. Journal of geodesy, 2019, 93(7): 1011-1024. DOI: 10.1007/s00190-018-1220-5 [8] 伍冠滨, 陈俊平, 伍晓勐, 等. 基于非差非组合PPP-RTK的大气改正模型及其性能验证[J]. 测绘学报, 2020, 49(11): 1407-1418. [9] 舒宝, 刘晖, 王利, 等. 区域参考站网支撑的PPP和RTK一体化服务及其性能[J]. 测绘学报, 2022, 51(9): 1870-1880. [10] 袁运斌, 侯鹏宇, 张宝成. GNSS非差非组合数据处理与PPP-RTK高精度定位[J]. 测绘学报, 2022, 51(7): 1225-1238. [11] WANG S Y, LI B F, TU R, et al. Uncertainty estimation of atmospheric corrections in large-scale reference networks for PPP-RTK[J]. Measurement, 2022(190): 110744. DOI: 10.1016/j.measurement.2022.110744 [12] 张宝成, 柯成, 查九平, 等. 非差非组合PPP-RTK: 模型算法、终端样机与实测结果[J]. 测绘学报, 2022, 51(8): 1725-1735. [13] 张小红, 胡家欢, 任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较[J]. 测绘学报, 2020, 49(9): 1084-1100. [14] 郭树人, 刘成, 高为广, 等. 卫星导航增强系统建设与发展[J]. 全球定位系统, 2019, 44(2): 1-12. [15] 商庆华, 成芳, 沈朋礼, 等. PPP-RTK模糊度快速固定算法研究[J]. 全球定位统, 2020, 45(6): 21-26. [16] 邓志旭, 付元辰, 李昕. 低轨增强北斗PPP-RTK定位方法与实验分析[J]. 全球定位系统, 2023, 48(1): 57-63. [17] 查九平. 非差非组合PPP-RTK区域网数据处理理论方法及应用研究[D]. 北京: 中国科学院大学, 2023. [18] ODIJK D, ZHANG B C, KHODABANDEH A, et al. On the estimability of parameters in undifferenced, uncombined GNSS network and PPP-RTK user models by means of S-system theory[J]. Journal of geodesy, 2016, 90(1): 15-44. DOI: 10.1007/S00190-015-0854-9 [19] ZHANG B C, YUAN Y B. PPP-RTK by means of S-system theory: revisiting the undifferenced, uncombined network model and a case study[C]//EGU General Assembly Conference Abstracts, 2017: 12221. [20] 李成钢, 黄丁发, 周乐韬, 等. GPS/VRS 参考站网络的对流层误差建模技术研究[J]. 测绘科学, 2007, 32(4): 29-31. [21] PSYCHAS D, VERHAGEN S, TEUNISSEN P J G. Precision analysis of partial ambiguity resolution-enabled PPP using multi-GNSS and multi-frequency signals[J]. Advances in space research, 2020, 66(9): 2075-2093. DOI: 10.1016/j.asr.2020.08.010 [22] ODIJK D, TEUNISSEN P J G. ADOP in closed form for a hierarchy of multi-frequency single-baseline GNSS models[J]. Journal of geodesy, 2008, 82(8): 473-492. DOI: 10.1007/S00190-007-0197-2 [23] TEMIISSEN J G. The least-squares ambiguity decorrelation adjustment: A method for fast GPS integer ambiguity estimation[J]. Journal of geodesy, 1995, 70(1): 65-82. DOI: 10.1007/BF00863419 [24] 侯鹏宇, 张宝成, 刘腾, 等. CDMA+FDMA非差非组合区域PPP-RTK[J]. 测绘学报, 2023, 52(2): 183-194. -




 下载:
下载: