Application research of gray model in unmanned motion target localization
-
摘要: 针对北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)在无人机定位中由于信号过弱或干扰过强而无法正常运行的问题，提出一种基于灰色理论的无人机预定位方法，以解决数据不完整情况下的轨迹坐标预测问题. 该方法利用灰色模型GM(1,1)灰色微分的连续性，根据无人机的历史离散数据建立了坐标点预测模型，利用实测数据验证了该模型的有效性，并通过仿真实验量化分析了灰色模型在定位预测的精确度，计算了其误差概率. 通过与传统定位方式对比可知，该模型所需要的数据量较少且计算方便，实现复杂度较低.Abstract: A method based on grey theory is proposed to solve the problem of unmanned moving target positioning caused by weak signals or strong interference in the BeiDou Navigation System (BDS). The method uses the grey model GM(1,1) to establish a coordinate prediction model based on the historical discrete data of unmanned moving targets, and verifies the validity of the model using measured data. The accuracy of the grey model in positioning prediction is quantitatively analyzed through simulation experiments, and its error probability is calculated. Compared with traditional positioning methods, this model requires less data and is computationally convenient, with lower complexity.
-
Key words:
- gray model /
- unmanned motion target /
- simulation /
- track display /
- position prediction.
-
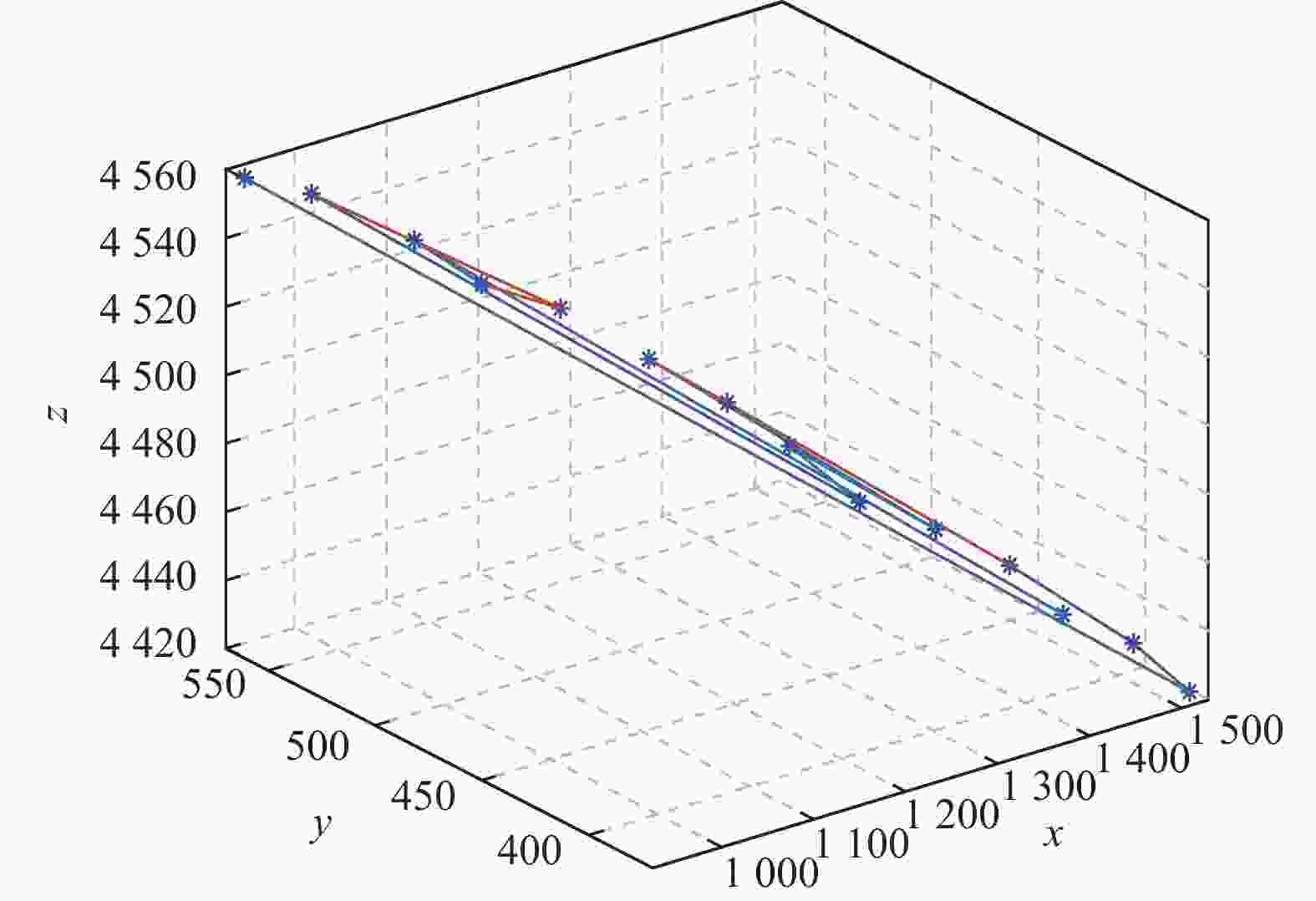
表 1 无人机的先期位置数据
坐标 t1 t2 t3 t4 t5 t6 t7 t8 t9 t10 t11 t12 t13 t14 x(i) 1 443 1 051 1 080 1 138 988 1 303 1 266 1 351 1 190 1 231 1 413 1 494 1 527 927 y(i) 401 536 517 505 557 436 453 421 486 467 413 390 378 562 z(i) 4 442 4 540 4 531 4 523 4 552 4 475 4 489 4 468 4 510 4 500 4 455 4 433 4 420 4 560 
下载: 导出CSV
表 2 灰色模型算法实现步骤
输入: 原始序列${X^{(0)}}$，预测序列的个数m
输出: 预测序列值${\hat X^{(0)}}$，预测精度p(k)
步骤1: 随机生成一组无序的原始非负数序列${X^{{\text{(0)}}}} = {\text{(}}{x^{{\text{(0)}}}}{\text{(1)}},{x^{{\text{(0)}}}}{\text{(2)}},{x^{{\text{(0)}}}}{\text{(3)}}, \cdots ,{x^{{\text{(0)}}}}{\text{(}}n{\text{))}}$；
步骤2: 对原始序列${X^{(0)}}$进行级比，$ \sigma (k)=\displaystyle\frac{{X}^{(0)}(k-1)}{{X}^{(0)}(k)}\begin{array}{cc}, k=2,3\cdots \end{array}(\sigma (k)\in ({\text{e}}^{-\frac{2}{n+1}},{\text{e}}^{\frac{2}{n+1}})) $，若满足级比条件，则进行第3步，否则对原始序列${X^{(0)}}$进行预处理并重复步骤2，直至满足级比条件；
步骤3: 将原始序列${X^{(0)}}$进行一次累加得到一个新的递增序列${X^{(1)}}$；
步骤4:将累加一次后的序列${X^{(1)}}$进行均值处理生成累加生成算子，由此得到紧邻值生成数列${Z^{(1)}} = ({z^{(1)}}(2),{z^{(1)}}(3),{z^{(1)}}(4), \cdot \cdot \cdot ,{z^{(1)}}(n))$，其中${z^{(1)}}(k) = \displaystyle\frac{1}{2}\left( {{x^{(1)}}(k) + {x^{(1)}}(k - 1)} \right)$；
步骤5: 建立灰色预测模型为${x^{(0)}}(k) + a{z^{(1)}}(k) = b$；
步骤6: 利用回归分析估计发展系数a，灰作用量b；
步骤7: 由此得预测值为$ {\hat{x}}^{(1)}(k+1)=\left({x}^{(0)}(1)-\displaystyle\frac{b}{a}\right){\text{e}}^{-ak}+\displaystyle\frac{b}{a}, k=1,2,\cdots, n-1 $；
步骤8: 将预测值进行累减得原序列预测值：$ {\hat x^{(0)}}(k + 1) = \begin{array}{*{20}{c}} {{{\hat x}^{(1)}}(k + 1) - {{\hat x}^{(1)}}(k)},&{k = 1,2, \cdots, n - 1} \end{array} $
步骤9: 根据所得到的原序列预测值即可计算预测精度：$ p(k) = \displaystyle\frac{{{x^{(0)}}(k) - {{\hat x}^{(0)}}(k)}}{{{x^{(0)}}(k)}},k = 1,2,3, \cdots, n $
下载: 导出CSV
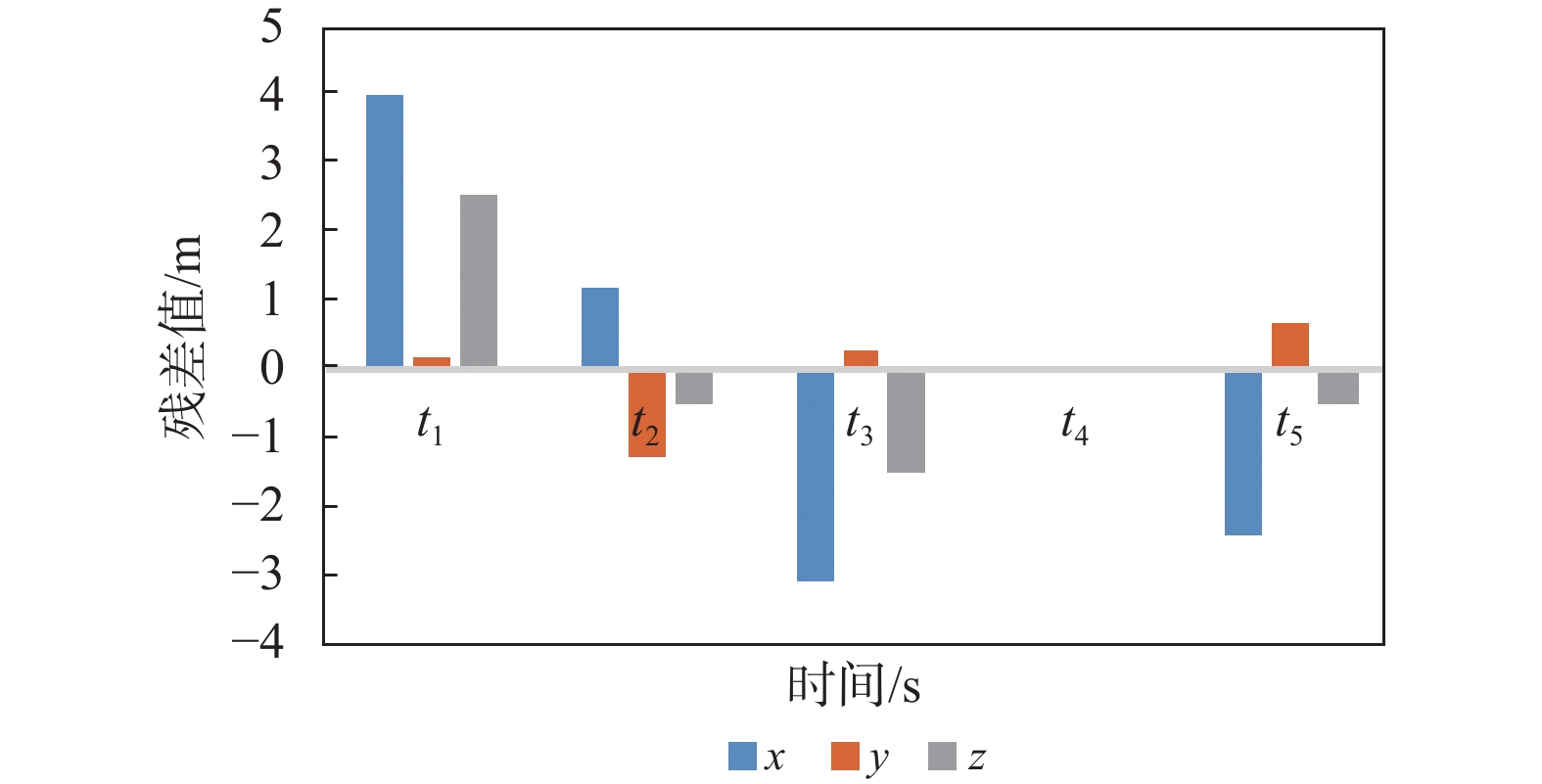
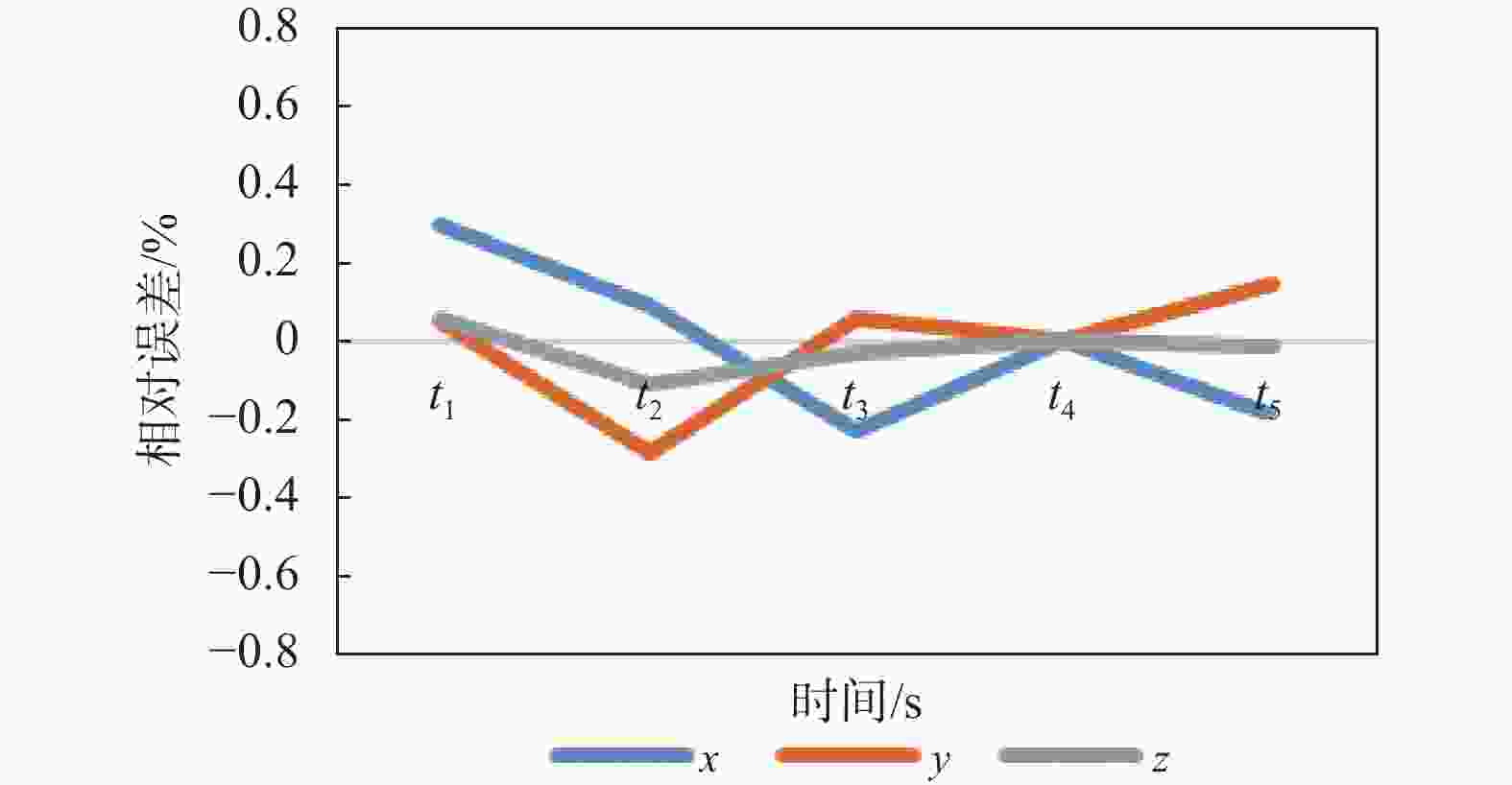
表 3 无人机坐标预测残差检验
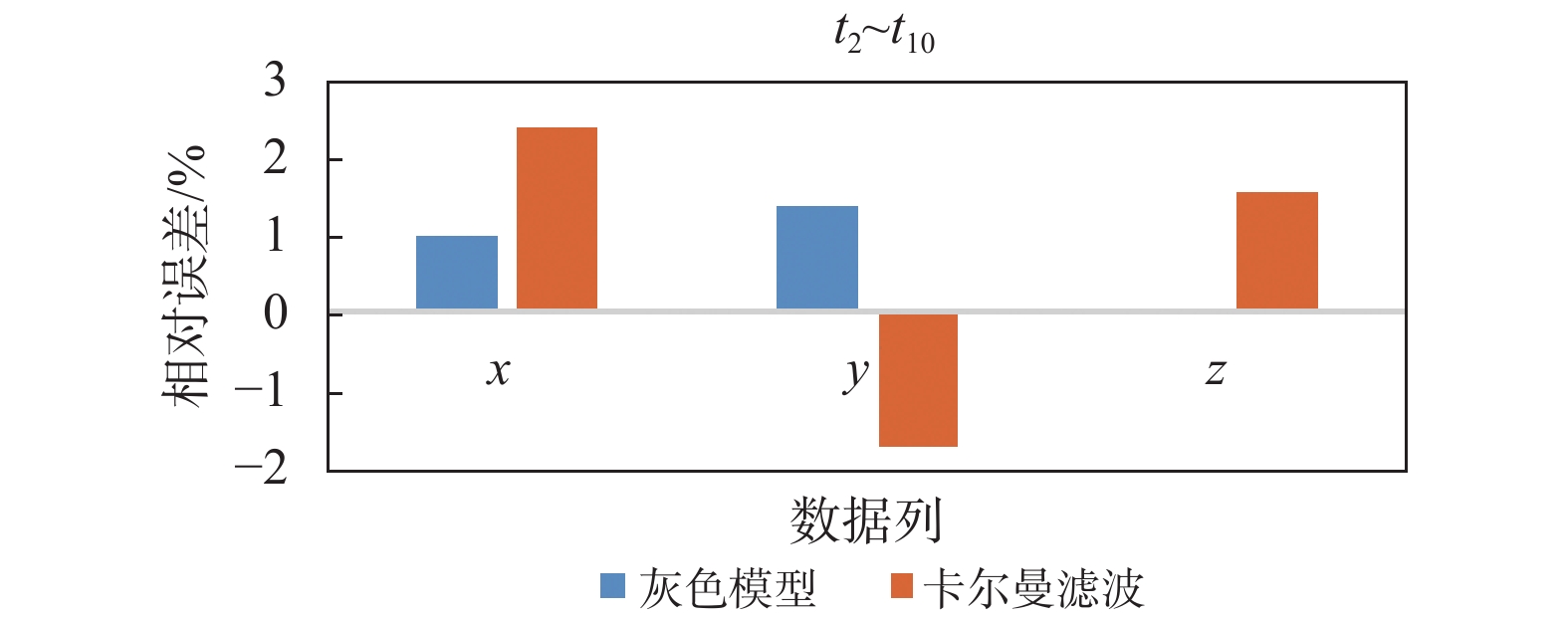
时刻 x(i) y(i) z(i) 原始数据 模型值 残差 相对误差/% 原始数据 模型值 残差 相对误差/% 原始数据 模型值 残差 相对误差/% t6 1 303 1 306.9 3.9 0.300 436 436.2 0.2 0.05 4 475 4 477.5 2.5 0.055 t7 1 266 1 267.2 1.2 0.091 453 451.7 −1.3 −0.29 4 489 4 488.5 −0.5 −0.011 t8 1 351 1 347.9 −3.1 −0.230 421 421.3 0.3 0.06 4 468 4 466.5 −1.5 −0.033 t9 1 190 1 190.0 0 0 486 486.0 0 0 4 510 4 510.0 0 0 t10 1 231 1 228.6 −2.4 −0.190 467 467.7 0.7 0.15 4 500 4 499.5 −0.5 −0.011 t11 - 1 390.2 - - - 406.8 - - - 4 455.6 - -
下载: 导出CSV
表 4 卡尔曼滤波相对误差
% 坐标 t6 t7 t8 t9 t10 x(i) 0 0.118 −0.152 0.171 −0.221 y(i) 0.028 0.157 0.158 −0.188 0.268 z(i) 0.072 0.165 −0.149 0.181 0.217
下载: 导出CSV
-
[1] 柯宏发, 刘思峰, 陈永光. 无人机飞行轨迹的实时显示预测算法[C]//北京: 第二十九届中国控制会议论文集, 2010. [2] 高普梅, 湛军. 基于扰动信息的连续区间灰数灰色预测模型[J]. 北京:系统工程与电子技术, 2019, 41(11): 34-36. [3] 韩亚坤, 周吕, 陈冠宇, 等. 灰色GM(1, 1)与KALMAN滤波模型用于变形预测的比较分析[J]. 地理空间信息, 2015, 13(2): 156-158. [4] 王鹏. 不确定性知识的灰色定性表达及其在机器人定位中的应用研究[D]. 合肥: 中国科学技术大学博士论文, 2015. [5] 刘思峰. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2023: 164-173. [6] 曹士龙. 城市中GPS卫星数不足四颗时定位技术研究[D]. 北京: 北京建筑工程学院硕士学位论文, 2012. [7] WANG J J, PARK J G. IEEE 802.11 WLAN based indoor positioning algorithm using weight grey prediction model[C]//The 22nd International Conference on High Performance Computing and Communications, 2020: 1158-1165. DOI: 10.1109/HPCC-SMARTCITY-DSS50907.2020.00150 [8] 王倩, 董燕, 宁德怀. 基于全球导航定位系统的滑坡变形监测分析与灰色模型预测研究[J]. 浙江农业科学, 2017, 58(9): 1629-1632. [9] 张艳秋, 花春亮, 赵亮. 基于灰色-最小二乘法的无人机交叉定标方法[J]. 地理信息世界, 2021, 28(4): 54-57. DOI: 10.3969/j.issn.1672-1586.2021.04.010 [10] 刘连义, 刘思峰, 姜爱平. 递归离散灰色模型及应用示例[J]. 系统工程理论与实践, 2023, 43(10): 3058-3068. [11] KANTUE P, PEDRO J O. Grey-box modelling of an unmanned quadcopter during aggressive maneuvers[C]//The 22nd International Conference on System Theory, Control and Computing (ICSTCC), 2018: 640-645. DOI: 10.1109/ICSTCC.2018.8540761 [12] 姜翠翠, 罗万春. 浅谈数学建模中的灰色预测GM(1, 1)模型的构建与应用[J]. 高等数学研究, 2023, 26(4): 31-33. [13] 黄卫华, 何佳乐, 陈阳, 等. 基于灰色模型和改进粒子滤波的无人机视觉/INS导航算法[J]. 中国惯性技术学报, 2021, 29(4): 459-466. -
点击查看大图
图(6) / 表(4)
计量
- 文章访问数: 63
- HTML全文浏览量: 14
- PDF下载量: 5
- 被引次数: 0
