Research on GNSS non-stationary interference technology for countering interference antennas
-
摘要: 针对GNSS抗干扰天线阵列,提出基于非平稳干扰信号的信号体制设计,以提高对GNSS信号的干扰效果. 通过构造针对GNSS抗干扰天线阵列的干扰场景,对不同体制的非平稳干扰信号进行仿真. 针对采用空频抗干扰算法的抗干扰天线,通过非平稳干扰信号对GNSS信号进行干扰,其干扰效果相对传统宽带扩频干扰,可以提高干扰效果在10 dB以上. 所设计的干扰体制的非平稳特性打破了天线阵列抗干扰算法设计的前提(干扰信号广义平稳),对此类抗干扰算法的性能产生较大影响.Abstract: A signal system design based on non-stationary interference signals is proposed for GNSS anti-interference antenna arrays to improve the interference effect on GNSS signals. Simulate non-stationary interference signals from different systems by constructing interference scenarios targeting GNSS anti-interference antenna arrays. For anti-interference antennas using space frequency anti-interference algorithms, the interference effect of GNSS signals is improved by more than 10 dB compared to traditional broadband spread spectrum interference by using non-stationary interference signals. The designed interference system, with its non-stationary characteristics, breaks the premise of designing antenna array anti-interference algorithms (the interference signal is generally stable), and has a significant impact on the performance of such anti-interference algorithms.
-
Keywords:
- anti-interference /
- non-stationary /
- GNSS /
- fourier transform /
- interference effect
-
0. 引 言
GNSS经过多年的发展,被广泛应用在民用及军用领域,由于其采用的技术手段和工作原理逐渐为人知悉,近年来对GNSS导航对抗的研究被广泛关注. 在军用领域普遍采用具备自适应抗干扰调零天线的接收机,以提高GNSS抗干扰能力. 针对GNSS导航对抗场景,自适应抗干扰天线的抗干扰算法已有很多研究,在更好的硬件平台支撑下,抗干扰算法不断完善与优化,抗干扰性能更好[1-2]. 而针对抗干扰天线的干扰方法的研究相对欠缺,采用分布式布站的方式,作为自适应抗干扰天线的干扰策略较为普遍[3-6],文献[7]研究了GNSS信号体制本身固有的抗干扰性能.
基于自适应调零天线的抗干扰算法是以非平稳干扰信号为基础进行设计,因此提出采用非平稳信号进行GNSS干扰,并对多种非平稳干扰信号与传统宽带干扰的干扰效果进行仿真,验证了采用非平稳干扰信号对抗GNSS抗干扰天线的有效性.
1. 针对自适应抗干扰调零天线的干扰策略
GNSS的干扰以及抗干扰不断进步[8-13],最新的干扰及抗干扰算法逐渐装备于军队中,在美军的GPS现代化规划中,已将自适应调零天线应用于GPS接收机中,从而提高接收机干扰容限. 作为一种显著提高GPS接收机抗干扰能力的手段,自适应调零天线可以对接收到的干扰信号形成空间零陷,从而最大限度地抑制该方向的干扰.
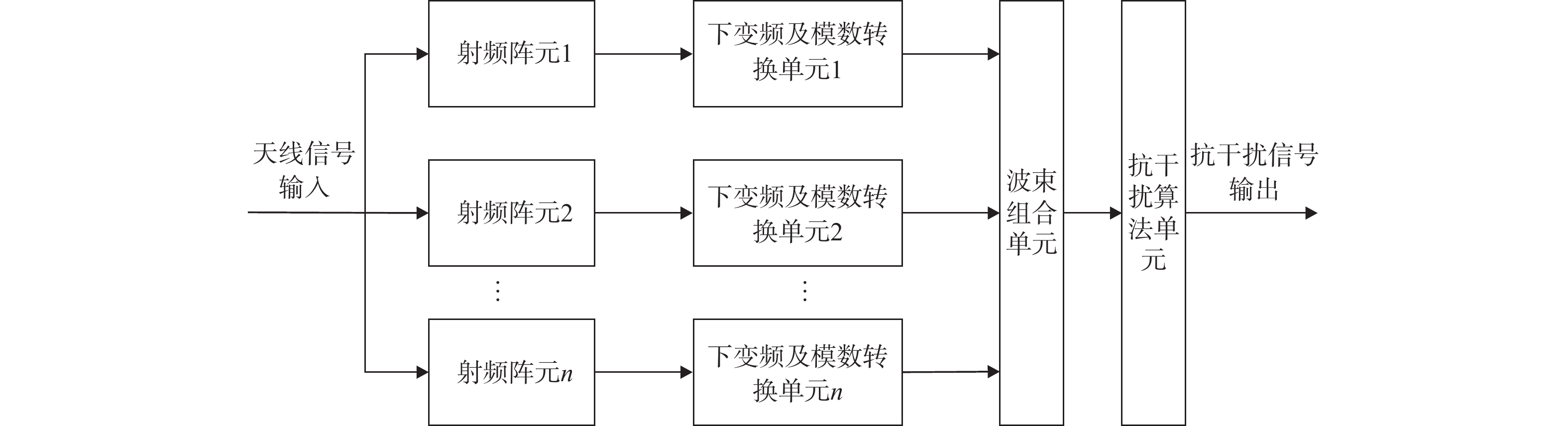
自适应调零天线通过对多个阵元设计特定的布局,对多个阵元分别设计信号处理通道,通过对多路信号赋权值,利用滤波的方式滤除干扰信号,获取期望信号. 自适应调零天线的组成框如图1所示.
在进行信号的分析处理时,可根据信号的平稳特征,将信号分为平稳信号以及非平稳信号. 对于平稳信号时间序列,其均值和方差是与时间无关的常数,协方差与时间无关,而与时间间隔有关. 利用样本时间序列所得到的拟合曲线,可在未来的一段时间内反映时间序列的均值、方差、协方差等信息. 对于非平稳信号时间序列,样本时间序列的本质特质只存在于当前发生的时间段内,其均值、方差、协方差不是常数,通过对该样本时间序列进行拟合的曲线,不足以反映该信号在未来时间段的特征信息.
对于统计特性随时间呈周期变化的信号,称为循环平稳随机过程,根据该信号的具体特征,可将该随机过程细分为严格平稳和广义平稳两种.
1)严格平稳过程
严格平稳随机过程的典型特点为:该信号的n个随机变量
$ \left\{ {{{X}}({t_1}),X({t_2}), \cdots ,X({t_n})} \right\} $ 以及其对应的$ \{ {X({t_1} + \tau ),} X({t_2} + \tau ), \cdots ,X({t_n} + \tau ) \} $ 的联合分布函数的时延$ \tau $ 均相同.2)广义平稳过程
当某个随机信号
$ \left\{ {X(t),t \in T} \right\} $ ,满足以下特点时,该信号为广义平稳随机过程.$$ E\left[ {X(t)} \right] = m, 为常数 $$ (1) $$ E\left[ {{{X}}{{(t)}^2}} \right] < \infty $$ (2) 式中,E为均值计算函数.
$$ \begin{aligned} E\left\{\right[X\left(t\right)-m\left]{\left[X\right(s)-m]}^{*}\right\}=&E\left[X\right(t\left){X}^{*}\right(s\left)\right]-m \\=&{R}_{x} (t-s)-m \\=&{R}_{x} (t,s)-m \end{aligned} $$ (3) 式中,
$ R $ 为相关计算函数.对该信号进行自相关计算,相应的自相关函数对于时延
$ \tau = 0 $ 共轭对称,可表示为$$ R_x^*( - \tau ) = {R_x}(\tau ) $$ (4) 对该信号进行功率谱密度计算,功率谱密度可表示为
$$ {P}_{x}^{*}\left(f\right)={P}_{x}\left(f\right)\geqslant 0 $$ (5) 式中,
$ P $ 表示功率计算函数.该信号是一种功率有限的信号,可表示为
$$ E\left[ {{{X}}{{\left( t \right)}^2}} \right] = {R_x}(0)\int_{ - \infty }^\infty {{P_x}(f){\rm{d}}f} < \infty $$ (6) 将该信号输入到线性时不变系统,输出仍是平稳随机信号,对应的时频函数可表示为:
$$ Y(t)=X(t)*h(t)= {\int }_{-\infty }^{\infty }X\left(u\right)h(t-u){\rm{d}}u $$ (7) $$ {P}_{y}\left(f\right)=H{\left(f\right)}^{2}{P}_{x}\left(f\right) $$ (8) 式中:Y表示时频响应;
$ H(f) $ 是冲激响应$ h(t) $ 的傅里叶变换.目前绝大多数调零天线的抗干扰算法,如空域、空时以及空频自适应处理算法,都是基于干扰信号广义平稳这一假设,即干扰信号的均值为常数,其协方差矩阵与时间起点无关,只与时间间隔有关. 因此,如果采用非平稳干扰信号体制,其均值或协方差是时变的,通过单纯的频率分析(傅里叶变换)不具备较好的时频分辨能力,也无法精确地对干扰信号进行定位. 此外,干扰信号的非平稳特性打破了天线阵列抗干扰算法设计的前提(干扰信号广义平稳),对此类抗干扰算法的性能产生较大影响. 因此,可采用非平稳干扰制式,对此条件下的干扰效果进行分析评估,验证非平稳干扰信号对GNSS抗干扰天线的干扰效果.
2. 非平稳干扰制式的仿真及干扰效果验证
空频抗干扰方法因其抗干扰性能较优,抗干扰算法的计算复杂度低,目前在军事和民用领域使用最为广泛,因此本仿真选择的GNSS调零天线的抗干扰方式为空频抗干扰方法. 通过仿真维纳过程、分段平稳信号、白噪声(white noise,WN)中时变正弦组合、均值具有趋向性的非平稳随机信号、周期平稳随机信号等非平稳信号的干扰效果,验证非平稳干扰信号应用于GNSS干扰策略的可行性.
2.1 仿真条件
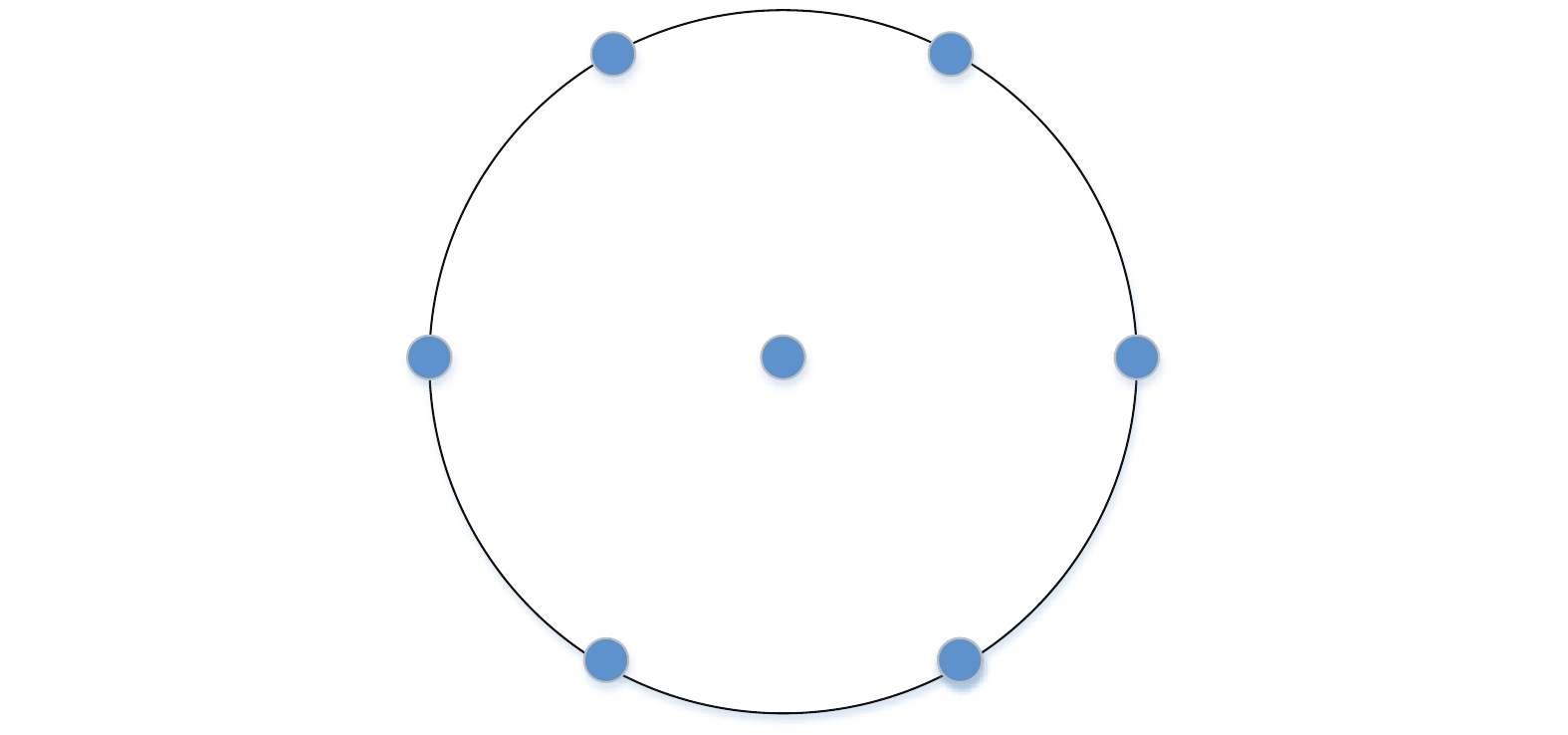
1)目前性能抗干扰性能最优的自适应抗干扰调零天线的阵元数量为7个,因此本仿真选择的阵列排布方式为七阵元圆阵,阵列排布如图2所示.
2)仿真的卫星方向及干扰方向如图3所示,卫星方向设置为方位角40°,俯仰角50°,扩频干扰和非平稳干扰方向均设置为方位角50°,俯仰角40°.
3)仿真的干扰信号频率覆盖1100 MHz~1600 MHz,该频段覆盖GNSS的各卫星导航系统,从而验证干扰制式对GNSS不同频率的干扰效果.
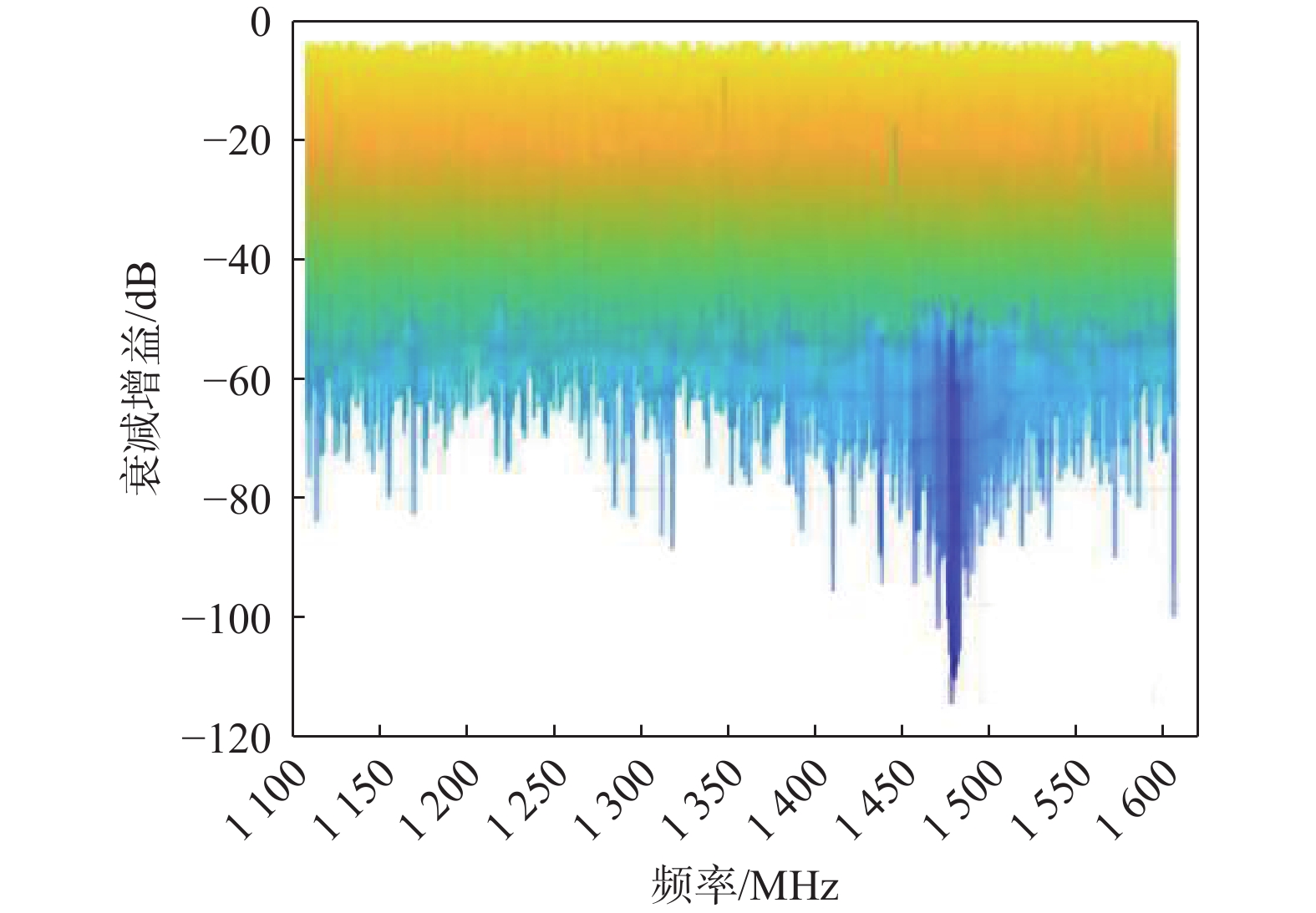
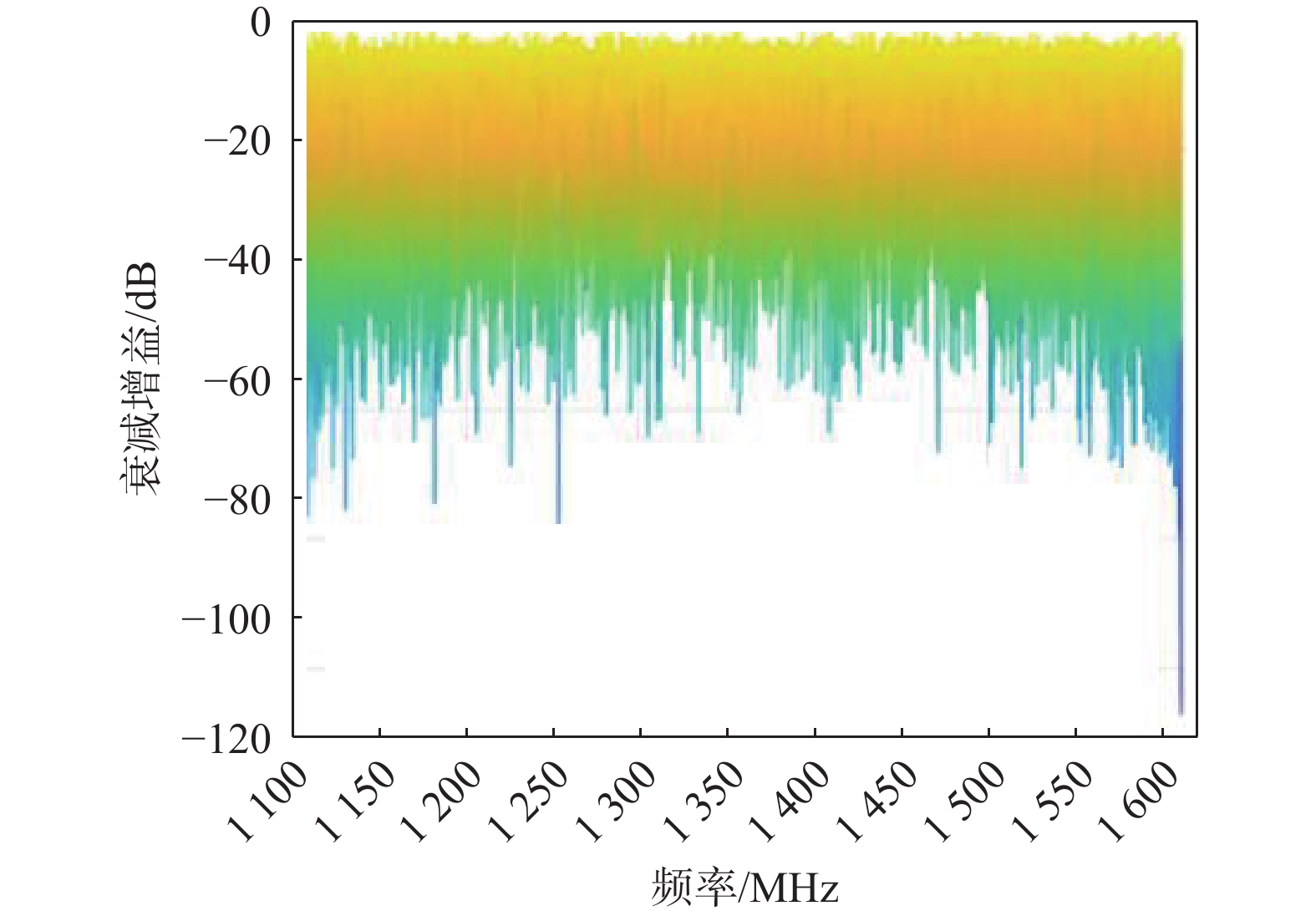
4)空频抗干扰方法对传统宽带扩频信号在干扰方向(方位角50°,俯仰角40°)的衰减增益随频率变化的情况如图4所示.
2.2 维纳过程干扰效果验证
将WN输入到一个积分器,其输出即为维纳过程. 维纳过程作为一种非平稳正态随机过程,若用
$ x(t) $ 来表示它,有$$ x(0) = 0 $$ (9) 其平均值与自相关函数可表示为
$$ \left\{ {\begin{array}{*{20}{l}} {E[x(t)] = 0} \\ {{r_{xx}}({t_1},{t_2}) = \left\{ {\begin{array}{*{20}{c}} {\alpha {t_2}({t_1} \geqslant {t_2})} \\ {\alpha {t_1}({t_1} < {t_2})} \end{array}} \right.} \end{array}} \right. $$ (10) 式中:
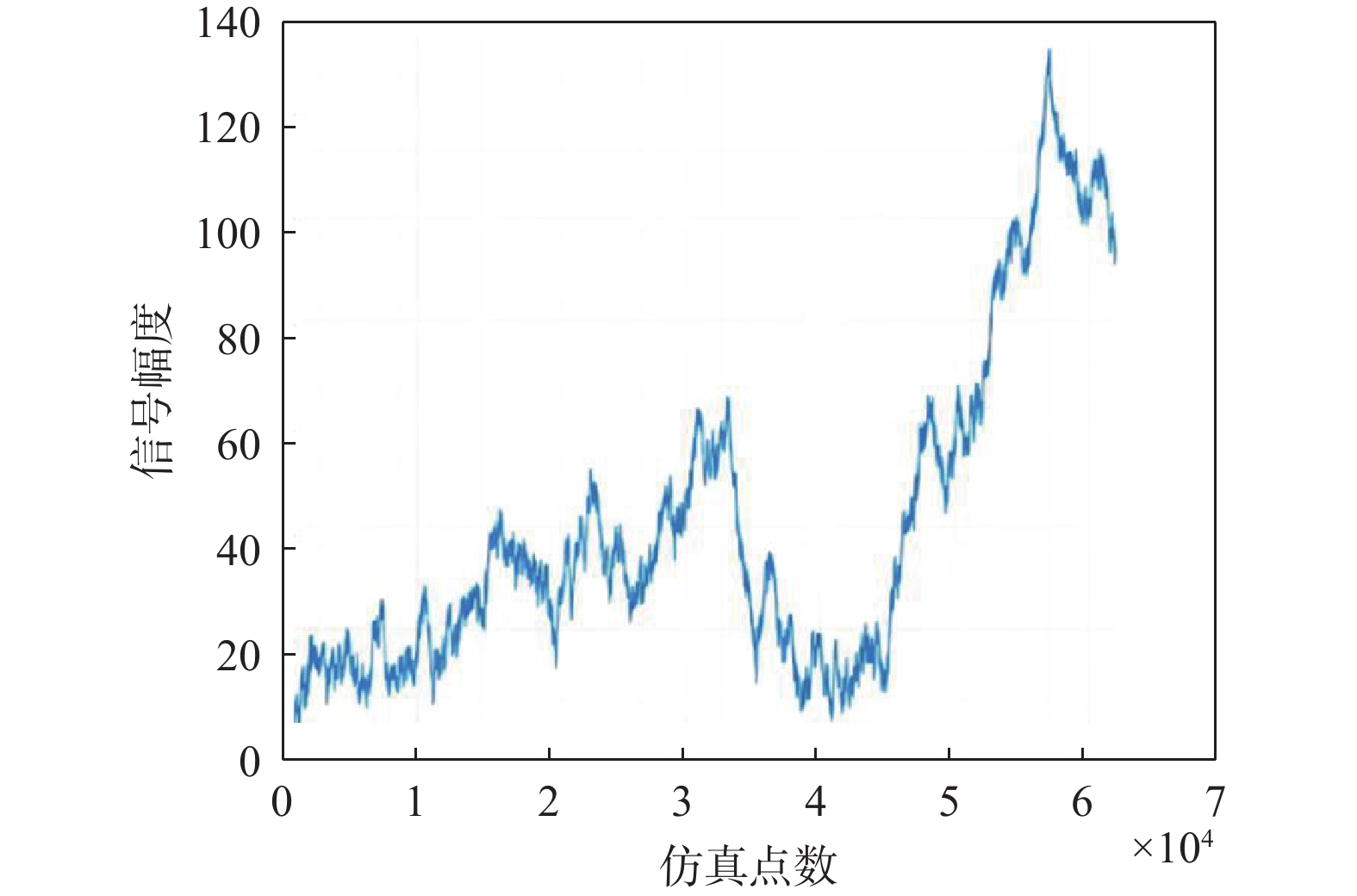
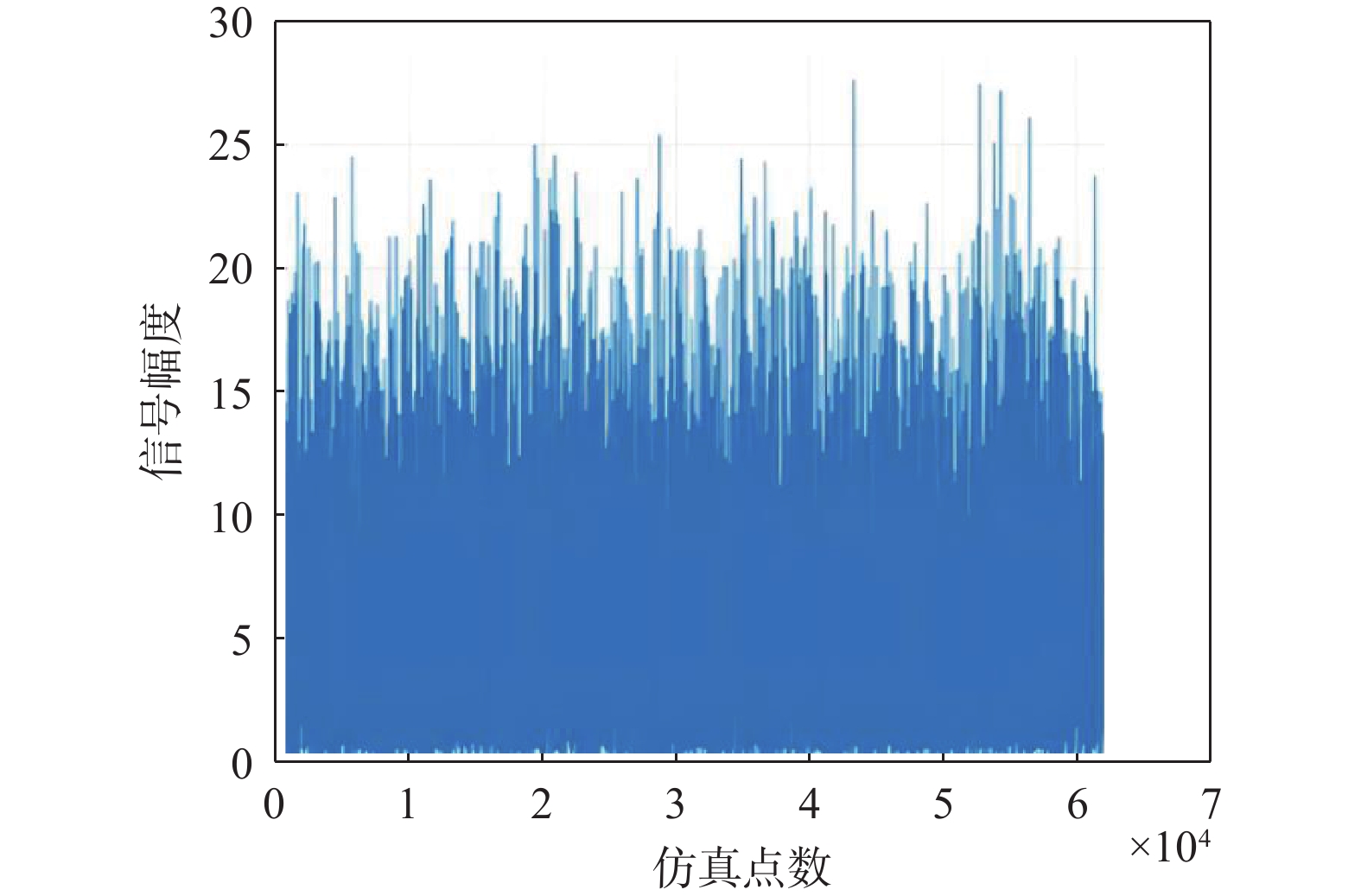
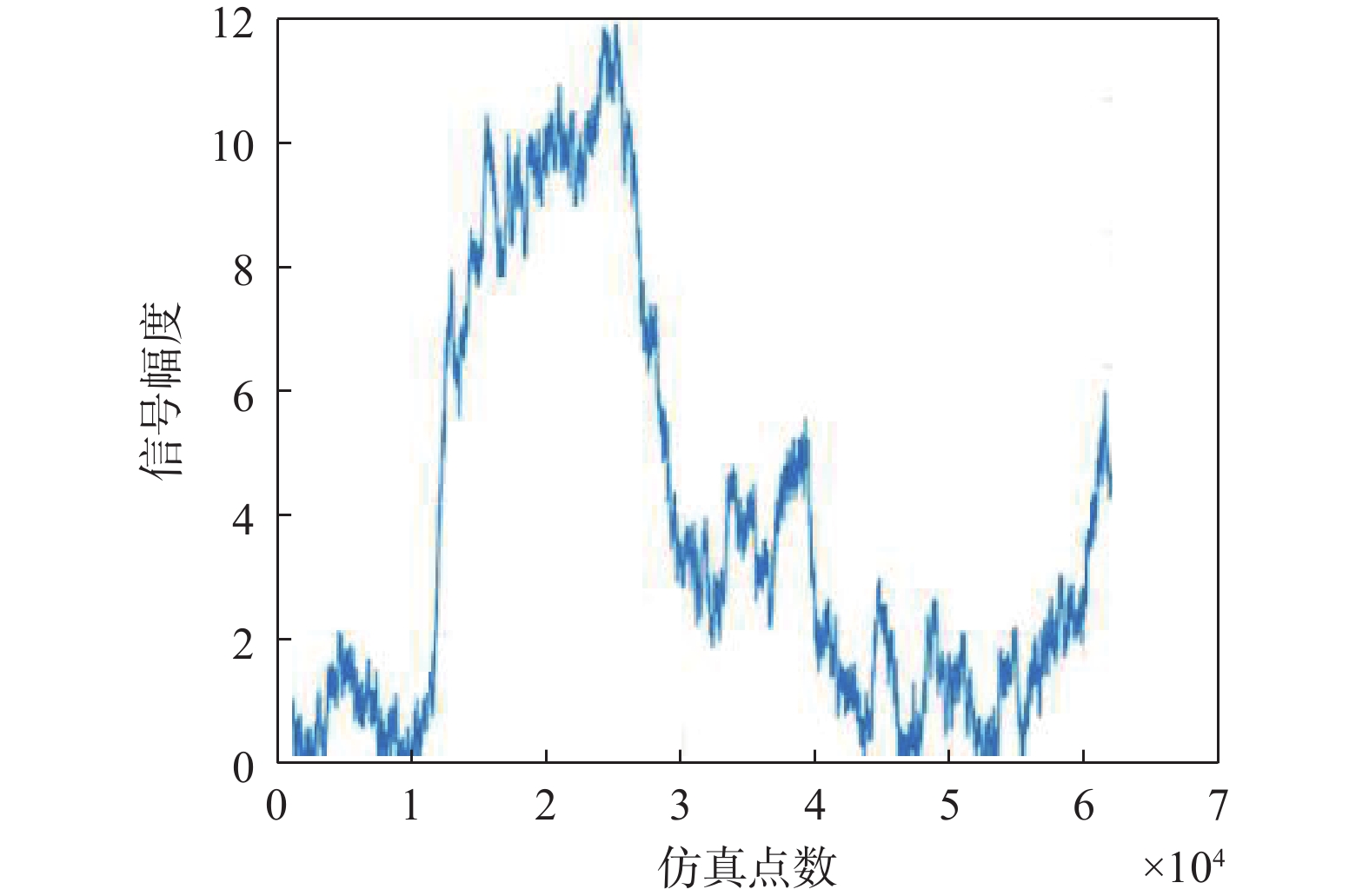
$ {r}_{xx} $ 为求自相关函数;$ \mathrm{\alpha } $ 为输入WN的方差. 若$ \omega (t) $ 为平稳正态WN,则维纳过程$ x(t) $ 为$$ x(t) = \int_0^t {\omega (\tau )} {\rm{d}}\tau $$ (11) 用维纳过程产生的非平稳信号进行仿真分析,其时域波形如图5所示.
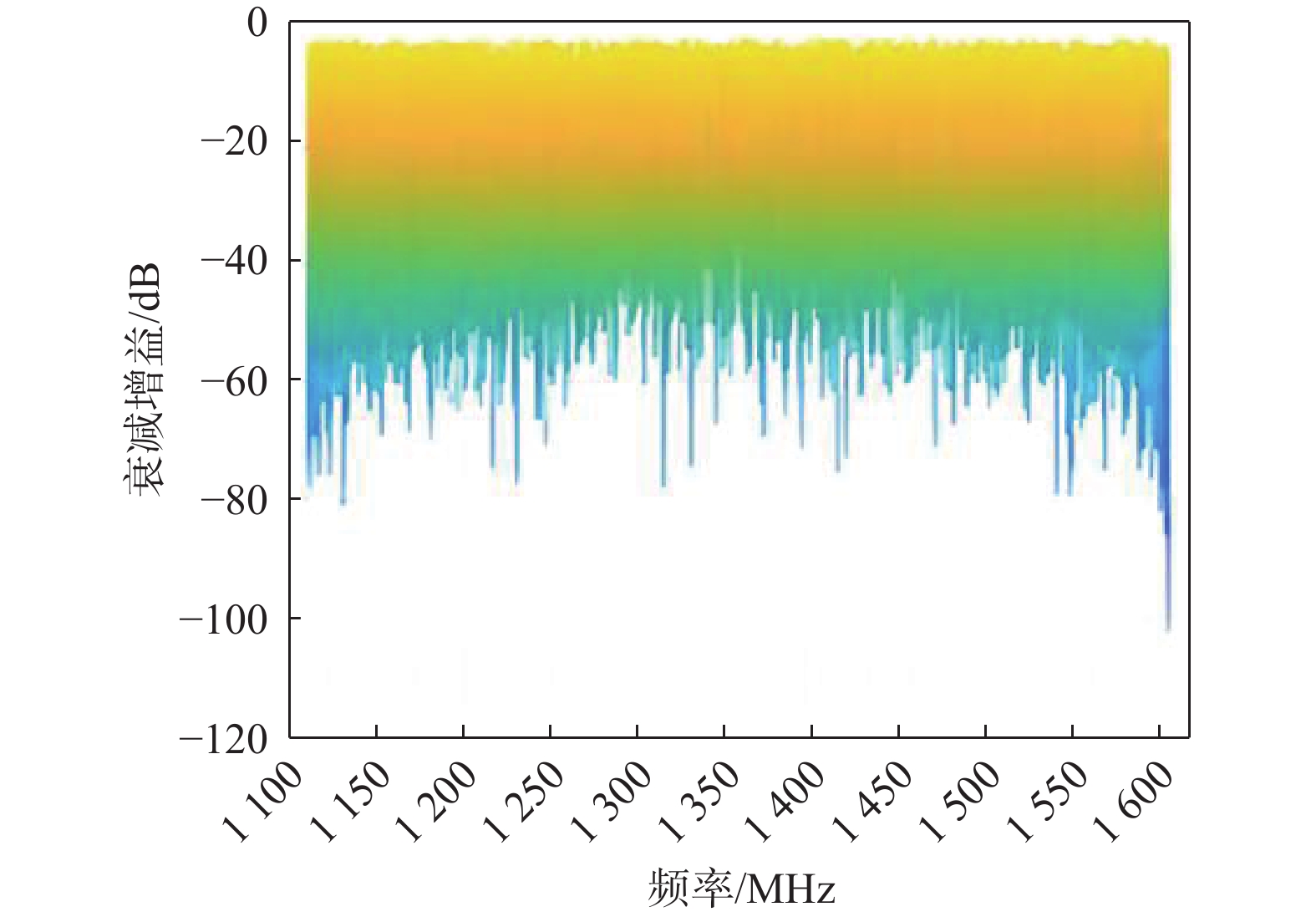
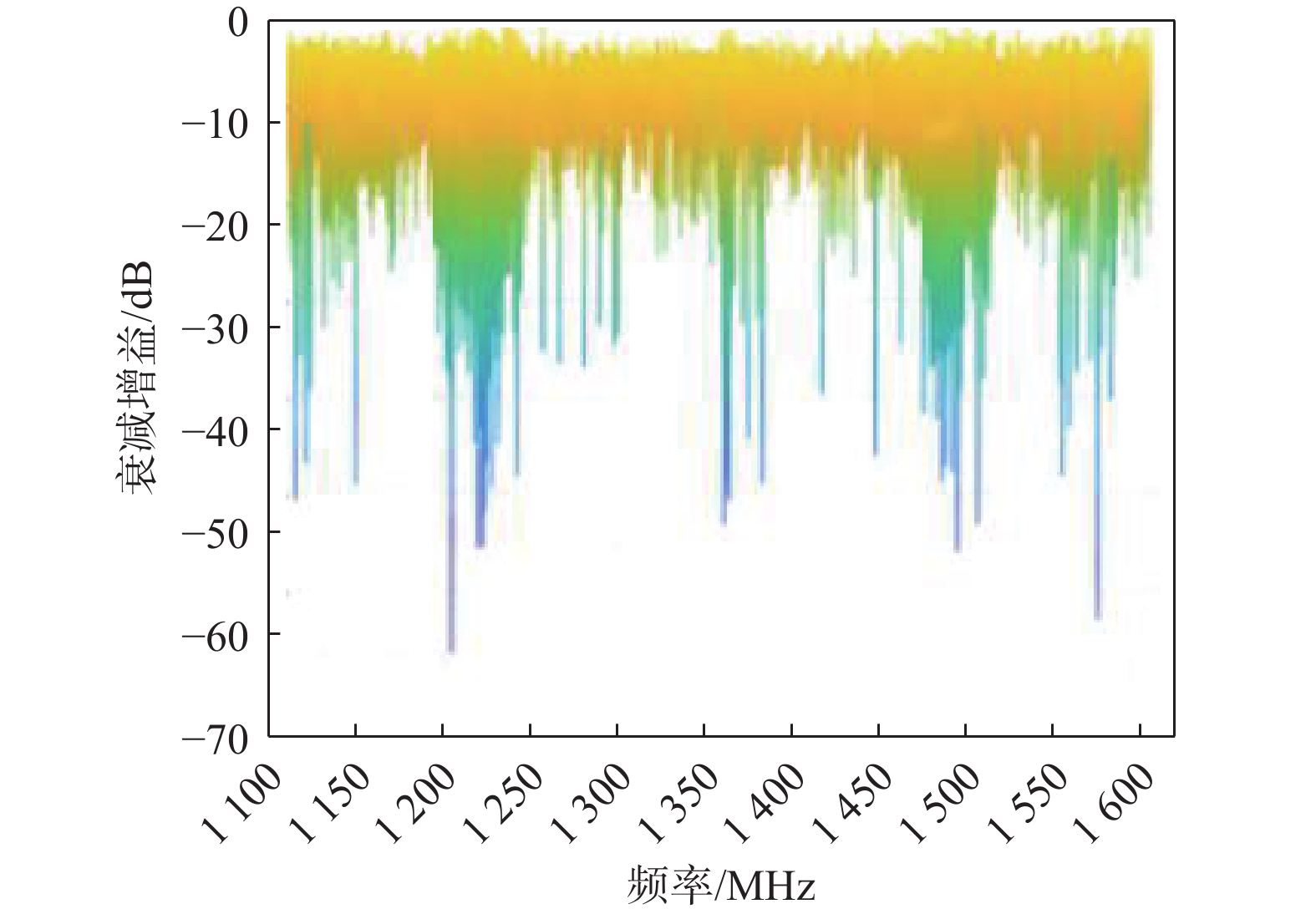
七阵元抗干扰调零天线对维纳过程非平稳信号干扰的衰减增益随频率的变化情况如图6所示.
通过与扩频信号干扰效果类比分析,可以非常明显的观察到采用维纳过程作为干扰信号,对空频抗干扰的干扰效果比扩频干扰的干扰效果好了10 dB以上,说明空频抗干扰对维纳过程非平稳干扰抑制能力较差.
2.3 分段平稳信号干扰效果验证
对于分段平稳随机信号,在完整的观测周期中,该信号的统计特征为非平稳的,但是在多个观测时刻,该信号会有统计特征的突变,如果将信号以突变时刻为分割点,切分为多个时间段进行分析,每段时间内信号的统计特征则保持着平稳特性.
对各段平稳随机信号可采用不同的平稳随机信号模型来描述其统计特性,通常采用自回归模型(autoregressive model,AR)进行信号仿真,将WN输入到线性时不变稳定系统,则输出即为分段平稳随机信号.
将AR(P)模型的
$ x(n) $ 表示为$$ x(n) = {a_{p,1}}x(n - 1) + {a_{p,2}}x(n - 2) + \cdots + {a_{p,p}}x(n - p) + \omega (n) $$ (12) 式中,
$ \omega (n) $ 为零均值与方差$ \delta _\omega ^2 $ 的正态WN.分别对
$ p $ =2、$ p $ =3以及它们的组合信号进行仿真分析,得到的分段平稳信号如图7所示.七阵元抗干扰调零天线对分段平稳信号干扰的衰减增益随频率的变化情况如图8所示.
通过与扩频信号干扰效果类比分析,采用分段平稳信号作为干扰信号,对空频抗干扰的干扰效果比扩频干扰的干扰效果低了15 dB以上,说明空频抗干扰对分段平稳信号的抑制能力较好.
2.4 时变正弦信号干扰效果验证
时变正弦组合是指恒定或时变幅值与时变频率的正弦波,其中恒定幅值与线性时变频率的正弦波为通常的线性调频(linear frequency modulation,LMF)信号.
2.4.1 固定幅值与时变频率的正弦波干扰仿真
为研究方便起见,令固定幅值为1与取样间隔
$ \Delta t=1 $ ,设时变频率的正弦波为$$ x(n) = \sin [\theta (n)] $$ (13) 式中,
$ \theta (n) $ 为相位函数.$ \theta (n) $ 是时变的,可表示为$$ \theta(n)=\theta (n-1)+\Delta \theta (n) $$ (14) 经过推导后可得:
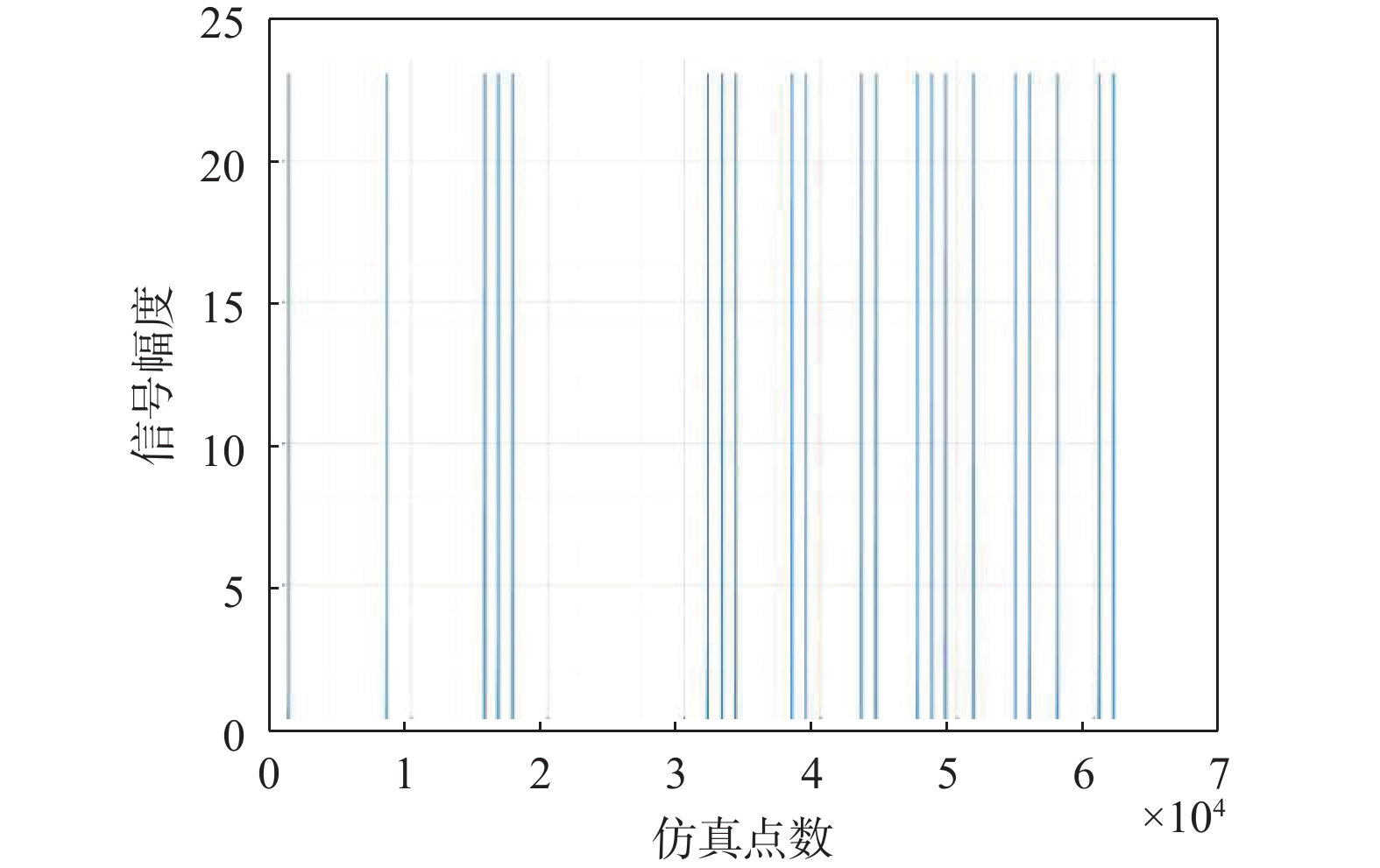
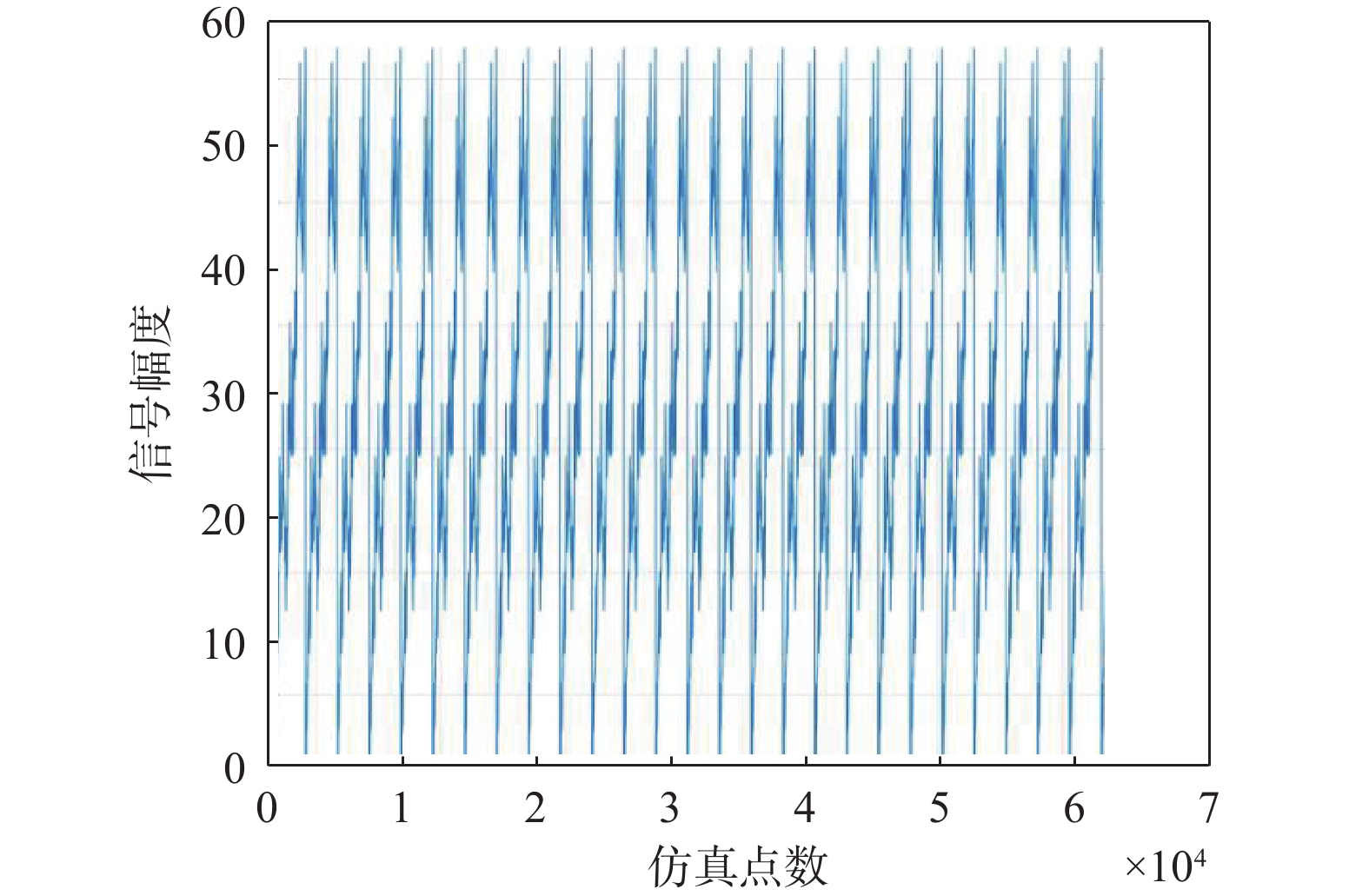
$$ x\left(n\right)={a}_{1}\left(n\right)x\left(n-1\right) -{a}_{2}\left(n\right)x\left(n-2\right) $$ (15) $$ {a}_{1}\left(n\right)=\frac{\mathrm{s}\mathrm{i}\mathrm{n}[\Delta \theta \left(n\right)+\Delta \theta (n-1\left)\right]}{\mathrm{s}\mathrm{i}\mathrm{n}[\Delta \theta (n-1\left)\right]} $$ (16) $$ {a}_{2}\left(n\right)=\frac{\mathrm{s}\mathrm{i}\mathrm{n}[\Delta \theta \left(n\right)]}{\mathrm{s}\mathrm{i}\mathrm{n}[\Delta \theta (n-1\left)\right]} $$ (17) 对固定幅值与时变频率的正弦波模型进行仿真分析,固定幅值与时变频率的正弦波模型的非平稳信号如图9所示.
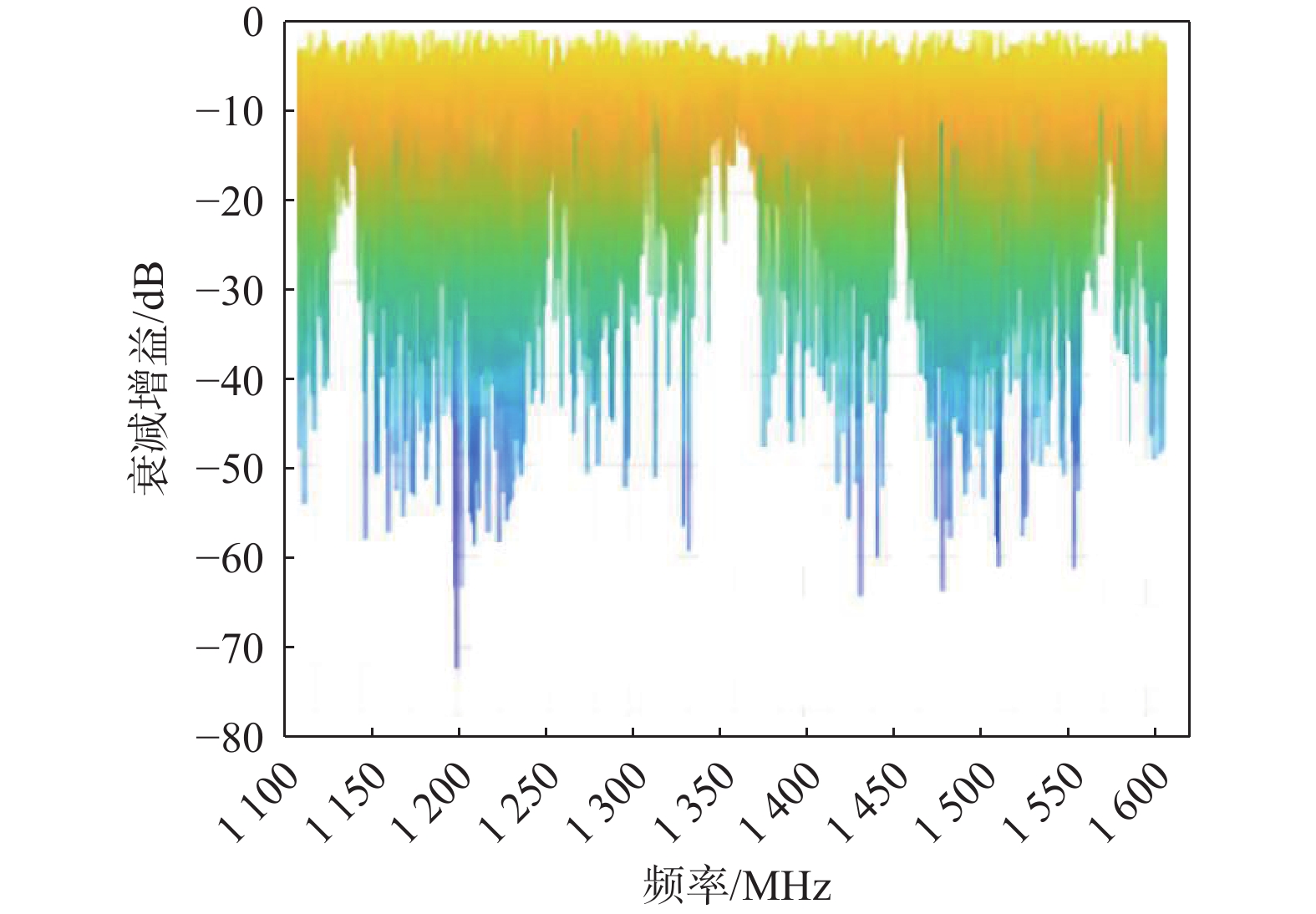
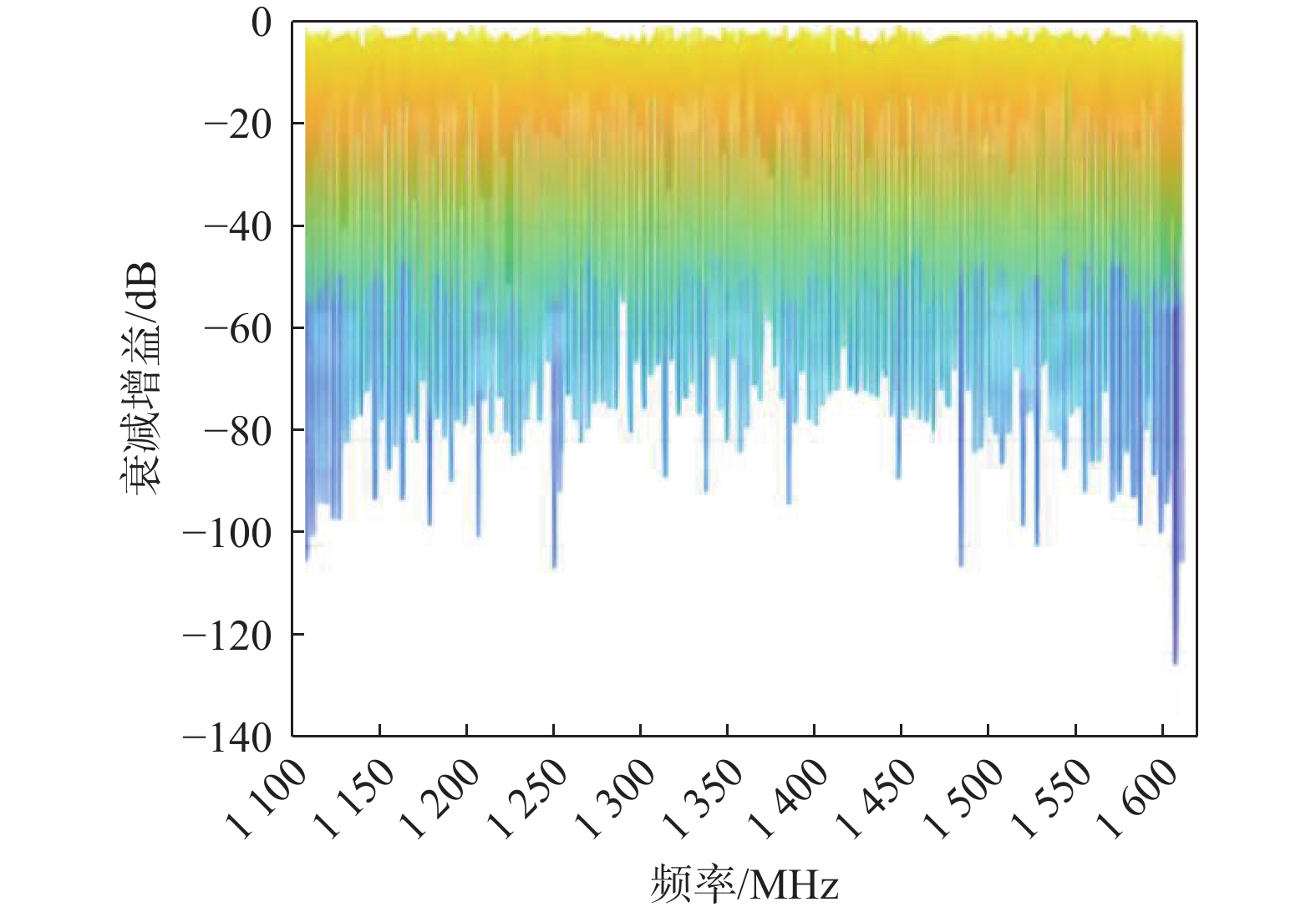
七阵元抗干扰调零天线对固定幅值与时变频率的正弦波信号干扰的衰减增益随频率的变化情况如图10所示.
通过与扩频信号干扰效果类比分析,采用固定幅值与时变频率的正弦波信号作为干扰信号,在大部分频段对空频抗干扰的干扰效果比扩频干扰的干扰效果提升约15 dB,但是存在少部分频段与扩频干扰有相似的干扰效果.
进一步考虑固定幅值与时变频率的正弦波信号间断出现的干扰方式,仿真结果图如图11~12所示.
可以发现固定幅值与时变频率的正弦波间断信号比干扰信号连续出现时的干扰能力更好一点,但还是在部分频段存在被抗干扰的风险.
2.4.2 时变幅值与时变频率正弦波干扰仿真
设具有时变幅值与时变频率的正弦波为
$$ x(n) = q(n)\sin [\theta (n)] $$ (18) 式中,
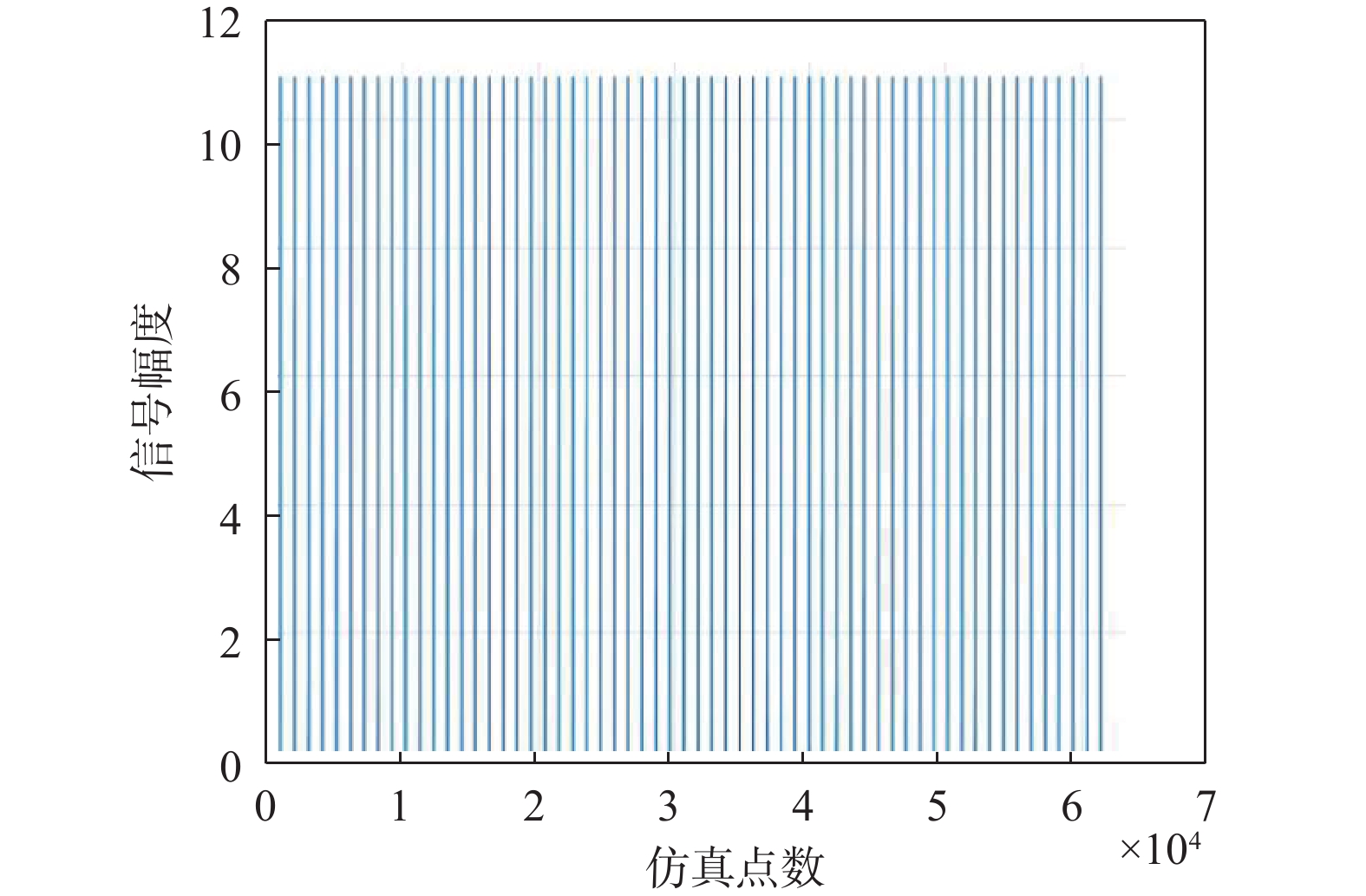
$ q(n) $ 为时变幅值函数.$$ x\left(n\right)={c}_{1}\left(n\right)x\left(n-1\right)-{c}_{2}\left(n\right)x\left(n-2\right) $$ (19) $$ {c}_{1}\left(n\right)=\frac{q\left(n\right){{\rm{sin}}}\left[\Delta \theta \left(n\right)+\Delta \theta \left(n-1\right)\right]}{q\left(n-1\right){{\rm{sin}}}\left[\Delta \theta \left(n-1\right)\right]} $$ (20) $$ {c}_{2}\left(n\right)=\frac{q\left(n\right)\mathrm{s}\mathrm{i}\mathrm{n}[\Delta \theta \left(n\right)]}{q\left(n-2\right)\mathrm{s}\mathrm{i}\mathrm{n}[\Delta \theta (n-1\left)\right]} $$ (21) 对时变幅值与时变频率的正弦波模型进行仿真分析,时变幅值与时变频率的正弦波模型的非平稳信号如图13所示.
七阵元抗干扰调零天线对时变幅值与时变频率的正弦波信号干扰的衰减增益随频率的变化情况如图14所示.
通过与扩频信号干扰效果类比分析,采用时变幅值与时变频率的正弦波信号作为干扰信号,对空频抗干扰的干扰效果比扩频干扰的干扰效果提升约15 dB,说明空频抗干扰对时变幅值与时变频率的正弦波信号的抑制能力较差.
2.5 均值具有趋向性的非平稳随机信号干扰效果验证
均值具有趋向性的非平稳随机信号的特点是它的均值是在某一个趋向性曲线的周围随机波动的. 该信号为线性时不变系统,当输入为WN时,输出为均值具有趋向性的非平稳信号.
设线性时不变离散系统的脉冲响应为
$ h(k) $ ,它有n个极点,若输入为WN时,其输出为$$ \left\{\begin{gathered} h(k) = \sum\limits_{i = 1}^n {{c_i}{k^{i - 1}}} \\ x(k) = \sum\limits_{l = 0}^\infty {h(l)\omega (k - l)} \\ \end{gathered}\right. $$ (22) 对均值具有趋向性的非平稳随机信号模型进行仿真分析,固定幅值与时变频率的正弦波模型的非平稳信号如图15所示.
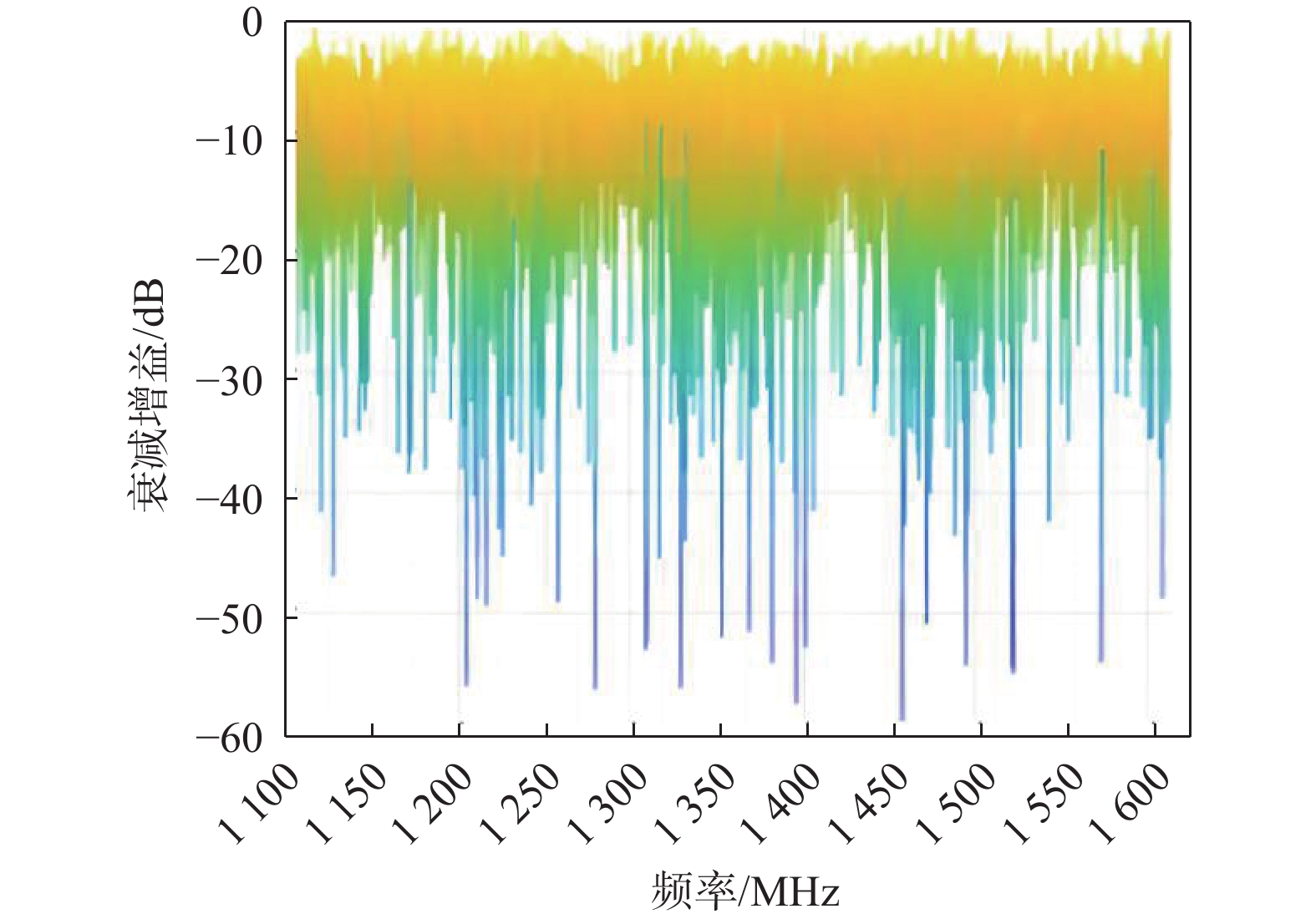
七阵元抗干扰调零天线对均值具有趋向性的非平稳随机信号干扰的衰减增益随频率的变化情况如图16所示.
通过与扩频信号干扰效果类比分析,采用均值具有趋向性的非平稳随机信作为干扰信号,对空频抗干扰的干扰效果比扩频干扰的干扰效果提升15 dB,说明空频抗干扰对均值具有趋向性的非平稳随机信号非平稳干扰抑制能力很差.
2.6 周期平稳随机信号干扰效果验证
周期平稳随机信号的典型特征为:其统计特征随时间周期性变化或近似周期性变化,该信号作为特殊的非平稳随机信号,可通过线性周期时变系统产生.
对于2阶非平稳信号
$ \left\{ {x(t)(t \in ( - \infty ,\infty ))} \right\} $ ,其均值和自相关函数均呈现以T为周期的周期性变化,即$$ \left\{ {\begin{array}{*{20}{l}} {{m_x}(t) = E[x(t)] = {m_x}(t + T)} \\ {{r_{xx}}(t) = E[x(t){x^*}(u)] = {r_{xx}}(t + T,u + T)} \end{array}} \right. $$ (23) 式中:
$ {m}_{x} $ (t)为均值函数;$ {r}_{xx} $ (t)为自相关函数.对该周期平稳随机信号进行仿真建模,周期平稳随机模型的非平稳信号如图17所示.
七阵元抗干扰调零天线对周期平稳随机信号干扰的衰减增益随频率的变化情况如图18所示.
通过与扩频信号干扰效果进行类比分析,采用均值具有趋向性的非平稳随机信作为干扰信号,对空频抗干扰的干扰效果与扩频干扰的干扰效果相似,只在部分频段比扩频干扰的干扰效果好.
3. 结束语
通过对多种典型非平稳干扰信号进行仿真,并对采用空频抗干扰方法的GNSS七阵元调零天线进行干扰效果验证. 对比非平稳干扰信号与扩频信号的干扰性能,优选出比扩频信号干扰效果更好的非平稳干扰信号如表1所示.
由表1可知,时变幅值与时变频率的正弦波信号,在仿真的GNSS频段中,都表现出较好的干扰性能. 因此,采用时变幅值与时变频率的正弦波作为干扰信号制式,可以有效对抗GNSS抗干扰天线.
表 1 非平稳信号干扰效果分析信号制式 相对扩频信号干扰衰减增益 干扰效果分析 维纳过程 大于10 dB 在GNSS整个频段比扩频干扰的干扰效果好10 dB 固定幅值与时变频率的正弦波 约15 dB 在GNSS部分频段与扩频干扰的干扰效果相似 固定幅值与时变频率的正弦波间断信号 大于15 dB 在GNSS部分频段相对扩频干扰的干扰效果好10 dB左右 时变幅值与时变频率的正弦波信号 大于15 dB 在GNSS个别频点相对扩频干扰的干扰效果好15 dB左右 均值具有趋向性的非平稳随机信号 约15 dB 在GNSS整个频段比扩频干扰的干扰效果好15 dB左右 -
表 1 非平稳信号干扰效果分析
信号制式 相对扩频信号干扰衰减增益 干扰效果分析 维纳过程 大于10 dB 在GNSS整个频段比扩频干扰的干扰效果好10 dB 固定幅值与时变频率的正弦波 约15 dB 在GNSS部分频段与扩频干扰的干扰效果相似 固定幅值与时变频率的正弦波间断信号 大于15 dB 在GNSS部分频段相对扩频干扰的干扰效果好10 dB左右 时变幅值与时变频率的正弦波信号 大于15 dB 在GNSS个别频点相对扩频干扰的干扰效果好15 dB左右 均值具有趋向性的非平稳随机信号 约15 dB 在GNSS整个频段比扩频干扰的干扰效果好15 dB左右 -
[1] 李津, 李鹏程, 刘博, 等 . 基于调零天线的无人机抗导航干扰方法[J]. 现代电子技术, 2023, 46(5): 25-28. [2] 郑建生, 陈鲤文, 代永红, 等. GNSS接收机抗干扰自适应调零技术性能估计[J]. 武汉大学学报, 2015, 40(8): 1006-1011. [3] 徐煦, 曾芳玲, 欧阳晓凤. 针对自适应调零接收机的卫星导航对抗装备运用策略研究[C]//第十届中国指挥控制大会论文集, 2023. [4] 白雪妨. 自适应调零天线对抗技术仿真研究[J]. 舰船电子对抗, 2023, 46(2): 35-39. [5] 毛虎, 吴德伟, 卢虎. 针对GPS接收机自适应天线调零抗干扰的对抗方法研究[J]. 弹箭与制导学报, 2016, 36(3): 99-103. DOI: 10.15892/j.cnki.djzdxb.2016.03.026 [6] 张教镭, 黄波. 相干干扰条件下阵列协方差矩阵退化分析[J]. 电子信息对抗技术, 2021, 36(1) : 18-22. [7] 毛虎, 吴德伟, 卢虎. GNSS信号体制抗干扰性能分析[J]. 电子科技大学学报, 2020, 49(4): 575-583. DOI: 10.12178/1001-0548.2018168 [8] 刘富, 舒展, 谢维华. 卫星导航对抗能力现状及发展趋势[J]. 导航定位学报, 2020, 8(6): 1-5. DOI: 10.3969/j.issn.2095-4999.2020.06.001 [9] 辛洁, 张天桥, 郭睿, 等. 卫星导航系统对抗体系构建方法研究[J]. 无线电工程, 2021, 51(10) : 1042-1047. DOI: 10.3969/j.issn.1003-3106.2021.10.005 [10] 焦博, 丛佃伟. 导航干扰技术在无人机防御中的应用展望[J]. 无线电工程, 2021, 51(10) : 1019- 1024. DOI: 10.3969/j.issn.1003-3106.2021.10.001 [11] 李亚伟. 针对采用阵列天线的卫星导航接收机干扰与抗干扰技术研究[D]. 西安: 西安电子科技大学, 2017. [12] 付钰, 朱克家, 韩奇, 等. 一种导航信号干扰源部署方法[J]. 导航定位学报, 2020, 8(3) : 110-114. [13] 张博, 何相勇, 赵丽华, 等. 高功率压制干扰模式下多个GPS干扰站联合部署问题[J]. 火力与指挥控制, 2018, 43(4): 32-36.



 下载:
下载: