Generalized damped LAMBDA method and the application in long baseline real-time positioning
-
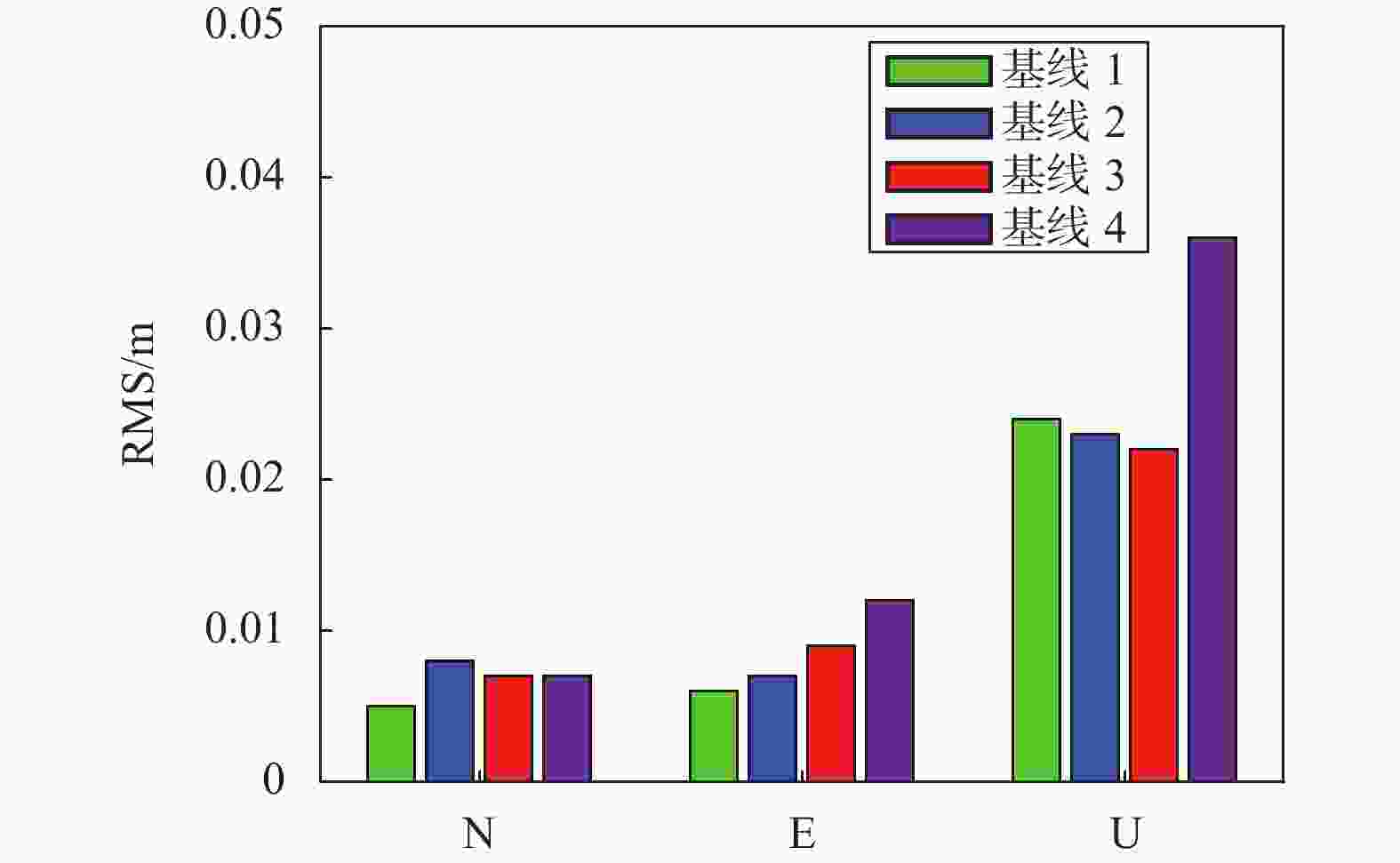
摘要: 在长基线实时定位中,相邻观测值之间具有强相关性导致法方程出现病态,此时载波相位整周模糊度难以快速固定. 针对这一问题,在传统阻尼最小二乘模糊度降相关平差(least-squares ambiguity decorrelation adjustment, LAMBDA)方法基础上,提出了广义阻尼LAMBDA方法,并推导出载波相位模糊度的单历元解表达式. 该方法利用了坐标和载波相位模糊度的先验信息,在改善法方程病态性的同时也提高了浮点模糊度的解算精度,有助于整周模糊度的快速固定. 采用两条长基线(266 km和456 km)实测数据进行验证,改进后的方法相比于传统方法,载波相位模糊度固定率提高了28.8%;当放大因子c=0时,广义阻尼LAMBDA方法与传统阻尼LAMBDA方法等价. 选择澳大利亚连续运行参考站系统(continuous operation reference system,CORS)网中四条长基线实时数据流进行测试,实验结果表明:在基线长度小于1 000 km的多系统实时定位中可以获得水平优于0.02 m,高程优于0.04 m定位精度. 基于广义阻尼LAMBDA方法在长基线实时定位中具有一定的应用参考价值.
-
关键词:
- 广义阻尼最小二乘模糊度降相关平差(LAMBDA) /
- 模糊度解算 /
- 长基线 /
- 实时定位
Abstract: In long baseline real-time positioning, strong correlation between adjacent observations resulting in ill-conditioned normal equation which is adverse to fast integer solution of carrier phase ambiguity. In this contribution, a generalized damped least-squares ambiguity decorrelation adjustment (LAMBDA) method was be proposed based on traditional LAMBDA method and the solution expression for carrier phase ambiguity in single epoch also be derived. This method uses the prior information of coordinates and carrier phase ambiguity to improve the ill-condition of the normal equation and the solution accuracy of floating ambiguity, which is helpful for the fast integer ambiguity solution. Two long baselines (266 km and 456 km) measured data were used to verify. Compared with the traditional method, the ambiguity fixed rate of the improved method was increased by 28.8%. When the amplification factor c=0, the generalized damped LAMBDA method was equivalent to the traditional damped LAMBDA method. Four long baseline real-time data streams from the Australian continuous operation reference system (CORS) network were selected for testing. The experimental results show that multi-system real-time positioning accuracy was better than 2 cm in the horizontal direction and 4 cm in the elevation direction with a baseline length of less than 1 000 km. The generalized damped LAMBDA method has certain application reference value for long baseline real-time positioning.-
Key words:
- generalized damped LAMBDA /
- ambiguity resolution /
- long baseline /
- real-time positioning
-
表 1 基线名称及长度
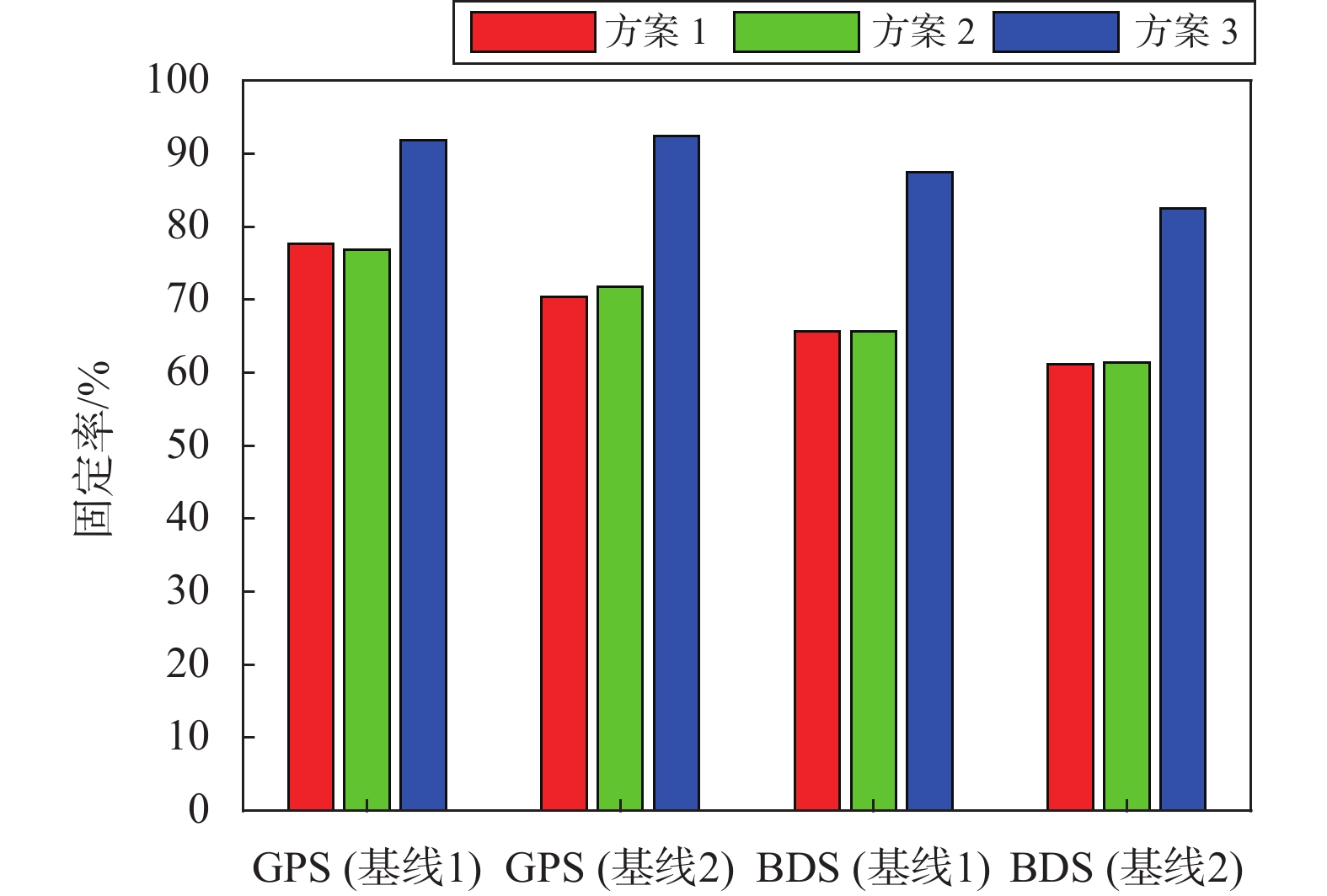
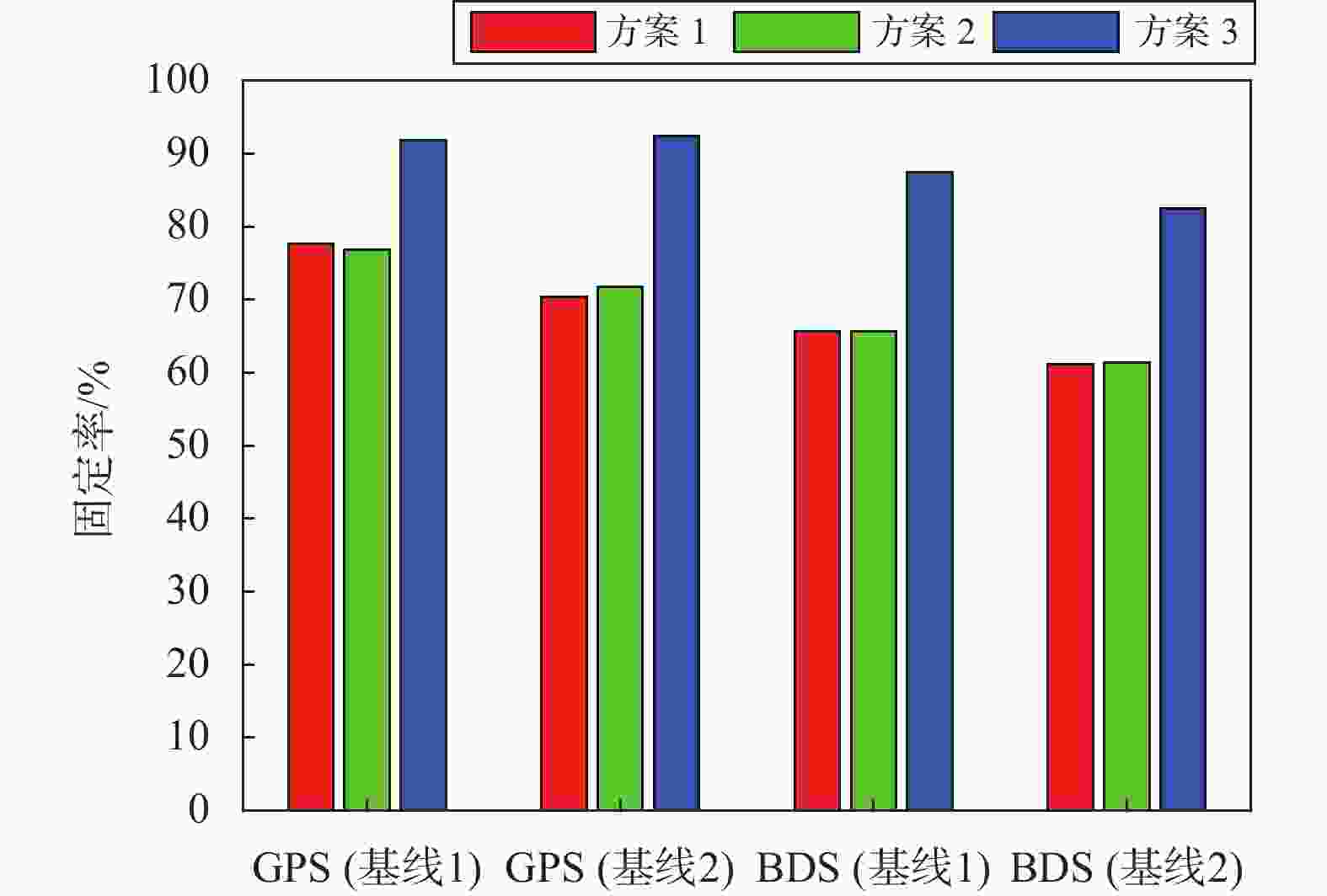
km 名称 测站 长度 基线1 STR1-PARK 266 基线2 STR1-MOBS 456 基线3 MCHL-PARK 736 基线4 MCHL-STR1 996 表 2 广义阻尼LAMBDA测试方案
方案 具体策略 方案1 传统阻尼LAMBDA方法 方案2 广义阻尼LAMBDA方法(全部c=0) 方案3 广义阻尼LAMBDA方法(高度角<30,
小数部分>0.25周时,c=0)表 3 实时长基线解算策略
项目 处理策略 定位模式 GPS+Galileo+BDS 观测频率 GPS:L1+L2; Galileo:E1+E5b; BDS:B1+B2 系统权比 GPS∶Galileo∶BDS=3∶3∶2 估计方法 Kalman滤波 高度角/采样率 15°、 1 s 待估参数 3个坐标分量、双差模糊度(载波伪距权比:100∶1)、天顶对流层延迟(GMF投影函数+随机游走过程噪声1.0 e−8m2/s) 电离层延迟 消电离层组合 卫星星历 广播星历+ CNES的SSR产品(5 s) 地球潮汐改正 IERS conventions2010 -
[1] ODOLINSKI R, TEUNISSEN P J G, ODIJK D. Combined BDS, Galileo, QZSS and GPS single-frequency RTK[J]. GPS solutions, 2015, 19(1): 151-163. DOI: 10.1007/s10291-014-0376-6 [2] SHI C, ZHAO Q L, HU Z G, et al. Precise relative positioning using real tracking data from COMPASS GEO and IGSO satellites[J]. GPS solutions, 2013, 17(1): 103-119. DOI: 10.1007/s10291-012-0264-x [3] 王生亮, 刘根友, 高铭, 等. GPS RTK/UWB紧组合精密动态定位性能分析[J]. 全球定位系统, 2021, 46(2): 69-76. [4] 祝会忠, 李军, 蔚泽然, 等. 长距离GPS/BDS参考站网多频载波相位整周模糊度解算方法[J]. 测绘学报, 2020, 49(3): 300-311. [5] TEUNISSEN P J G, JONGE P D , TIBERIUS C C J M. The least-squares ambiguity decorrelation adjustment: its performance on short GPS baselines and short observation spans[J]. Journal of geodesy, 1997, 71(10): 589-602. DOI: 10.1007/s001900050127 [6] 孙妍艳, 刘翠芝. 基于自适应差分进化算法的高维模糊度搜索[J]. 全球定位系统, 2018, 43(1): 36-42. [7] TEUNISSEN P J G. GPS carrier phase ambiguity fixing concepts[M]. GPS for Geodesy, Springer, Berlin, Heidelberg, 1998: 319-388. [8] 曹士龙, 刘根友, 王生亮, 等. GPS超长基线解算的误差特性与精度分析[J]. 武汉大学学报(信息科学版), 2023, 48(2): 260-267. [9] 张钰玺, 张小红, 刘全海, 等. 航空测量场景下的中长基线动态定位方法[J]. 测绘学报, 2019, 48(7): 871-878. [10] 于文浩, 张云, 韩彦岭, 等. 北斗三频中长基线差分定位性能研究[J]. 全球定位系统, 2018, 43(4): 102-109. [11] 金星, 王玲, 黄文德, 等. 一种单频单历元BDS/GPS组合整周模糊度解算方法[J]. 全球定位系统, 2018, 43(1): 75-80. [12] 易重海, 陈源军. 顾及历元间坐标差信息的GPS模糊度快速固定改进方法[J]. 武汉大学学报(信息科学版), 2019, 44(4): 489-494. [13] BRACK, A. Reliable GPS + BDS RTK positioning with partial ambiguity resolution[J]. GPS solutions, 2017, 21(1): 1083-1092. DOI: 10.1007/810291-016-0594-1 [14] 舒宝, 刘晖, 张晋升, 等. 基于BDS/GPS组合定位的部分模糊度固定效果分析[J]. 武汉大学学报(信息科学版), 2017, 42(7): 989-994, 1001. [15] LI P, ZHANG X. Precise point positioning with partial ambiguity fixing[J]. Sensors, 2015, 15(6): 13627-13643. DOI: 10.3390/s150613627 [16] 高旺, 高成发, 潘树国, 等. 基于部分固定策略的多系统长距离基准站间模糊度快速解算[J]. 武汉大学学报(信息科学版), 2017, 42(4): 558-562. [17] 刘根友, 朱耀仲, 韩保民. GPS单历元定位的阻尼LAMBDA算法[J]. 武汉大学学报(信息科学版), 2004, 29(3): 195-197. -




 下载:
下载: