Comparison and analysis of GNSS precision point positioning performance based on DCB and OSB products
-
摘要: 随着全球卫星导航系统(GNSS)的不断建设,精密单点定位(PPP)可用频率和通道逐步多元化. 文中在原始观测方程的基础上,分别推导出适用于差分码偏差(DCB)产品和绝对偏差(OSB)产品的双频无电离层组合(IF)PPP模型,并利用50个MGEX (Multi-GNSS Experiment)测站的10 d连续观测数据对两种策略对比分析了各GNSS系统PPP模型的定位性能. 结果表明:采用OSB产品的PPP模型在性能上与传统的DCB产品差异可以忽略不计,而且OSB产品在使用时更便利,更适合未来多频PPP的应用前景.Abstract: With the development of the Global Navigation Satellite System (GNSS), the channels and frequencies used for precision point positioning (PPP) are gradually diversified. Therefore, based on the original observation equations, this study derived the dual-frequency ionosphere-free (IF) PPP model for differential code bias (DCB) and observable-specific signal bias (OSB) products, respectively, and used 10-day continuous observation data collected from 50 Multi-GNSS Experiment (MGEX) stations to analyze the performance of the PPP model for each GNSS system. The results show that the performance of PPP model using the OSB product is consistent with that of the conventional DCB product, and the OSB product is more convenient to use and has more applications in future multi-frequency PPP.
-
0. 引 言
目前,以GPS、GLONASS、Galileo以及北斗卫星导航系统(BDS)为主的全球卫星导航系统(GNSS)趋于成熟,为全球用户提供高精度、高可靠的位置服务. 我国的BDS由于建设阶段性的原因,主要分为北斗二号全球卫星导航系统(BDS-2)以及北斗三号全球卫星导航系统(BDS-3)两部分[1],并且已有研究表明,在BDS-2和BDS-3间存在时延偏差问题,不能将两者当成一个系统使用[2].
精密单点定位(PPP)技术以其独立性、无需基站的特点受到国内外众多学者的研究,PPP模型也由传统的单频或双频单系统发展成多频多系统[3]. 然而,多频多系统的PPP技术也带来了一系列的新偏差,如卫星端的差分码偏差(DCB)问题. Wang等[4]采用IGGDCB方法估计各GNSS的卫星端DCB产品,并验证了其精度与欧洲轨道确定中心(CODE)、德国航空航天中心(DLR)一致. 但是,随着越来越多的GNSS播发三频甚至四频、五频信号[5],DCB产品使用起来越来越麻烦. 因此,国际GNSS服务(IGS)组织提出绝对偏差(OSB)这一概念,并通过相应的SINEX格式进行定义、应用和推广[6]. OSB产品可以直接在原始观测值上改正,不需要进行任何变换,在可用性方面具有很大的优势.
中国科学院(CAS)发布的DCB产品已经被广泛使用,但其新公开的OSB产品还没有被充分研究. 目前,CAS分别发布了顾及和不顾及天线相位中心(APC)改正的OSB产品,由于PPP技术涉及精密星历的使用,本文采用顾及APC改正的OSB产品,针对CAS发布的DCB和OSB两种产品分别进行各GNSS的双频PPP实验,验证两种产品在不同系统情况下的可用性及一致性,为未来多频多系统OSB产品的应用提供一定的参考.
1. 双频PPP模型
GNSS原始伪距和载波相位基本观测方程为[7]
$$ \left\{ \begin{array}{l} P_{{\rm{r}},j}^{\rm{s}} = \rho _{{\rm{r}}}^{\rm{s}} + c \cdot {\text{d}}{t_{\rm{r}}} - c \cdot {\text{d}}{t^{\rm{s}}} + {\text{TD}}{{\text{B}}^{\rm{C}}} + \\ \qquad\; {T_{\rm{r}}} + {\gamma _j} \cdot I_{{\rm{r}},1}^{\rm{s}} + c(d_{{\rm{r}},j}^{\rm{s}} - d_j^{\rm{s}}) + \varepsilon _{{\rm{r}},{P_j}}^{{\rm{s}},{\rm{T}}} \\ L_{{\rm{r}},j}^{\rm{s}} = \rho _{\rm{r}}^{\rm{s}} + c \cdot {\text{d}}{t_{\rm{r}}} - c \cdot {\text{d}}{t^{\rm{s}}} + {\text{TD}}{{\text{B}}^{\rm{C}}} + \\\qquad\; {T_{\rm{r}}} - {\gamma _j} \cdot I_{{\rm{r}},1}^{\rm{s}} + \lambda _j^{\rm{s}}(N_{{\rm{r}},j}^{\rm{s}} + b_{{\rm{r}},j}^{\rm{s}} - b_j^{\rm{s}}) + \xi _{{\rm{r}},{L_j}}^{\rm{s}} \end{array} \right..$$ (1) 式中:上标
${\rm{s}}$ 为G、R、E、C,分别代表GPS、GLONASS、Galileo、BDS,需要注意的是BDS包含了BDS-2和BDS-3,因此,当$ {\rm{s}} $ 表示BDS系统时,需要加入一个时延偏差项$ {\text{TDB}} $ ;下标$ {\rm{r}} $ 、$ j $ 为接收机和频率($ j $ =1,2);$ P $ 和$ L $ 为伪距和载波相位的原始观测值;$\;\rho _{\rm{r}}^{\rm{s}}$ 为接收机与卫星之间的几何距离;$ c $ 为光速;${\text{d}}{t_{\rm{r}}}$ 和${\text{d}}{t^{\rm{s}}}$ 分别为接收机钟差和卫星钟差;$ {\gamma _j} $ 为电离层因子,$ {\gamma _j} = f_1^2/f_j^2 $ ;$I_{{\rm{r}},1}^{\rm{s}}$ 为$ {f_1} $ 信号上的斜电离层延迟;${T_{\rm{r}}}$ 为测站天顶的对流层延迟;$\lambda _j^{\rm{s}}$ 为频率$ {f_j} $ 载波对应的波长;$N_{{\rm{r}},{\rm{j}}}^{\rm{s}}$ 为载波模糊度;$d_{{\rm{r}},j}^{\rm{s}}$ 和$d_j^{\rm{s}}$ 分别为接收机端和卫星端的非校正伪距硬件延迟(UCD);$b_{{\rm{r}},j}^{\rm{s}}$ 和$b_j^{\rm{s}}$ 分别为接收机端和卫星端的非校正相位硬件延迟(UPD);$\varepsilon _{{\rm{r}},{P_j}}^{{\rm{s}},{\rm{T}}}$ 和$\xi _{{\rm{r}},{L_j}}^{\rm{s}}$ 为伪距和载波相位的观测噪声、多路径效应以及其他未模型化误差之和;其他误差项(如天线相位中心改正、地球潮汐改正以及相对论效应等)已经采用相应的模型该正[8].为方便后续公式的推导,定义下列表达式:
$$ \left\{\begin{array}{l}{\alpha }_{mn}=\displaystyle\frac{{f}_{m}{}^{2}}{{f}_{m}^{2}-{f}_{n}^{2}},\;{\beta }_{mn}=-\frac{{f}_{n}{}^{2}}{{f}_{m}{}^{2}-{f}_{n}{}^{2}}\\ {\text{DCB}}_{mn}^{{\rm{s}}}\text={d}_{m}^{{\rm{s}}}-{d}_{n}^{{\rm{s}}},\;{\text{DCB}}_{{\rm{r}},mn}^{{\rm{s}}}={d}_{{\rm{r}},m}^{{\rm{s}}}-{d}_{{\rm{r}},n}^{{\rm{s}}}\\ {d}_{{\text{IF}}_{mn}}^{{\rm{s}}}={\alpha }_{mn}\cdot {d}_{m}^{{\rm{s}}}+{\beta }_{mn}\cdot {d}_{n}^{{\rm{s}}},{d}_{{\rm{r}},{\text{IF}}_{mn}}^{{\rm{s}}}={\alpha }_{mn}\cdot {d}_{{\rm{r}},m}^{{\rm{s}}}+{\beta }_{mn}\cdot {d}_{{\rm{r}},n}^{{\rm{s}}}\end{array}.\right. $$ (2) 式中:
$ \alpha _{mn}^{} $ 和$\;\beta _{mn}^{}$ 为双频无电离层组合(IF)因子;${\text{DCB}}_{mn}^{\rm{s}}$ 和${\text{DCB}}_{{\rm{r}},mn}^{\rm{s}}$ 分别为卫星端和接收机端的DCB;$d_{{\text{I}}{{\text{F}}_{mn}}}^{\rm{s}}$ 和$d_{{\rm{r}},{\text{I}}{{\text{F}}_{mn}}}^{\rm{s}}$ 分别为卫星端和接收机端的IF组合UCD.本文采用德国地学研究中心(GFZ)发布的精密星历产品计算卫星钟差,产品分别以GPS的L1/L2、GLONASS的G1/G2、Galileo的E1/E5a、BDS的B1I/B3I为基准频率生成[9],卫星钟差改正
${\text{d}}t_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}}$ 包含了卫星端的$d_{{\text{I}}{{\text{F}}_{mn}}}^{\rm{s}}$ ,则$$ c \cdot {\text{d}}t_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} = c[{\text{d}}{t^{\rm{s}}} + (\alpha _{12}^{} \cdot d_1^{\rm{s}} + \beta _{12} \cdot d_2^{\rm{s}})] = c({\text{d}}{t^{\rm{s}}} + d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}}). $$ (3) 式(1)经精密星历改正后,为
$$ \left\{ \begin{array}{l} P_{{\rm{r}},j}^{\rm{s}} = \rho _{{\rm{r}}}^{\rm{s}} + c \cdot {\text{d}}{t_{\rm{r}}} + {\text{TD}}{{\text{B}}^{\rm{C}}} + {T_{\rm{r}}} +{\gamma _j} \cdot I_{{\rm{r}},1}^{\rm{s}} +\\ \qquad \; c \cdot d_{{\rm{r}},j}^{\rm{s}} + c\left( {d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} - d_j^{\rm{s}}} \right) + \varepsilon _{{\rm{r}},{P_j}}^{{\rm{s}},{\rm{T}}} \\ L_{{\rm{r}},j}^{\rm{s}} = \rho _{\rm{r}}^{\rm{s}} + c \cdot {\text{d}}{t_{\rm{r}}} + {\text{TD}}{{\text{B}}^{\rm{C}}} + {T_{\rm{r}}} - {\gamma _j} \cdot I_{{\rm{r}},1}^{\rm{s}} + \\ \qquad \; \lambda _j^{\rm{s}}(N_{{\rm{r}},j}^{\rm{s}} + b_{{\rm{r}},j}^{\rm{s}} - b_j^{\rm{s}}) + c \cdot d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} + \xi _{{\rm{r}},{L_j}}^{\rm{s}} \end{array} \right.. $$ (4) 1.1 DCB产品的使用
通常,卫星端的DCB在一天内是不会变化的,需要使用MGEX (Multi-GNSS Experiment)发布的DCB产品对伪距偏差项
$d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} - d_j^{\rm{s}}$ 改正. 但是DCB代表的是频率间的伪距偏差,因此,不能直接在各频率的伪距观测方程上改正,具体方法为$$ \left\{ \begin{array}{l} d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} - d_1^{\rm{s}} = - \beta _{12} \cdot {\rm{DCB}}_{12}^{\rm{s}} \\ d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} - d_2^{\rm{s}} = \alpha _{12} \cdot {\rm{DCB}}_{12}^{\rm{s}} \\ \end{array} \right..$$ (5) 不难看出,DCB产品的使用需要搭配IF组合因子,在未来多频多系统的应用背景下,传统的DCB改正方法将会十分复杂困难.
1.2 OSB产品的使用
与DCB产品不同,OSB产品包含了每个频率上的绝对伪距偏差. CAS在产品服务端通过约束基准码进行DCB的估计[10],从而得到最终的OSB产品:
$$ \left\{ \begin{gathered} {\text{DCB}}_{12}^{\rm{s}} = d_1^{\rm{s}} - d_2^{\rm{s}} \\ d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} = \alpha _{12} \cdot d_1^{\rm{s}} + \beta _{12}^{} \cdot d_2^{\rm{s}} \\ d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} = 0 \\ \end{gathered} \right. \Rightarrow \left\{ \begin{gathered} {\text{OSB}}_1^{\rm{s}} = d_1^{\rm{s}} = \beta _{12}^{} \cdot {\rm{DCB}}_{12}^{\rm{s}} \\ {\text{OSB}}_2^{\rm{s}} = d_2^{\rm{s}} = - \alpha _{12}^{} \cdot {\rm{DCB}}_{12}^{\rm{s}} \\ \end{gathered} \right. .$$ (6) 可以看出,OSB产品是在DCB产品估计的基础上增加一个卫星端IF组合UCD等于0的约束求出的,在改正的时候是直接在伪距观测方程上减去相应的
$ {\text{OSB}}_j^{\rm{s}} $ .1.3 双频IF模型
无论是DCB还是OSB产品,原理上都是为了对原始伪距观测方程的伪距硬件延迟项
$d_{{{\rm{IF}}_{12}}}^{\rm{s}} - d_j^{\rm{s}}$ 改正,改正后的式(4)可表示为$$ \left\{ \begin{array}{l} P_{{\rm{r}},j}^{\rm{s}} = \rho _{{\rm{r}}}^{\rm{s}} + c \cdot {\text{d}}{t_{\rm{r}}} + {\text{TD}}{{\text{B}}^{\rm{C}}} + {T_{\rm{r}}} + {\gamma _j} \cdot \\\qquad\; I_{{\rm{r}},1}^{\rm{s}} + c \cdot d_{{\rm{r}},j}^{\rm{s}} + \varepsilon _{{\rm{r}},{P_j}}^{{\rm{s}},{\rm{T}}} \\ L_{{\rm{r}},j}^{\rm{s}} = \rho _{\rm{r}}^{\rm{s}} + c \cdot {\text{d}}{t_{\rm{r}}} + {\text{TD}}{{\text{B}}^{\rm{C}}} + {T_{\rm{r}}} - {\gamma _j} \cdot I_{{\rm{r}},1}^{\rm{s}} + \\\qquad\; \lambda _j^{\rm{s}}(N_{{\rm{r}},j}^{\rm{s}} + b_{{\rm{r}},j}^{\rm{s}} - b_j^{\rm{s}}) + c \cdot d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} + \xi _{{\rm{r}},{L_j}}^{\rm{s}} \end{array} \right..$$ (7) IF组合模型是最经典的PPP模型(式(8)),其特点是通过IF组合因子消除一阶电离层延迟的影响,具有模型简单易实现[11]、计算效率高等优点.
$$ \left\{\begin{array}{l}{P}_{{\rm{r}},{\text{IF}}_{12}}^{{\rm{s}}}={\alpha }_{12}\cdot {P}_{{\rm{r}},1}^{{\rm{s}}}+{\beta }_{12}\cdot {P}_{{\rm{r}},2}^{{\rm{s}}}={\rho }_{{\rm{r}}}^{{\rm{s}}}+\\\qquad\quad\; c\cdot {\bar{\text{d}}{t}_{{\rm{r}}}}+{\text{TDB}}^{{\rm{C}}}+{T}_{{\rm{r}}}+{\varepsilon }_{{\rm{r}},{\text{IF}}_{12}}^{{\rm{s}}}\\ {L}_{{\rm{r}},{\text{IF}}_{12}}^{{\rm{s}}}={\alpha }_{12}\cdot {L}_{{\rm{r}},1}^{{\rm{s}}}+{\beta }_{12}\cdot {L}_{{\rm{r}},2}^{{\rm{s}}}={\rho }_{r}^{{\rm{s}}}+ c\cdot {\bar{\text{d}}{t}_{{\rm{r}}}}+\\\qquad\quad\;{\text{TDB}}^{{\rm{C}}}+{T}_{{\rm{r}}}+{\bar{N}}_{{\rm{r}},{\text{IF}}_{12}}^{{\rm{s}}}+{\xi }_{{\rm{r}},{\text{IF}}_{12}}^{{\rm{s}}}\end{array},\right. $$ (8) $$ \left\{ \begin{array}{l} {\bar{\text{d}}{t_{\rm{r}}}} = {\text{d}}{t_{\rm{r}}} + d_{{\rm{r}},{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} \\ \bar N_{{\rm{r}},{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} = \alpha _{12}^{} \cdot \lambda _1^{\rm{s}}(N_{r,1}^{\rm{s}} + b_{{\rm{r}},1}^{\rm{s}} - b_1^{\rm{s}}) + \beta _{12} \cdot\\\qquad\quad \; \lambda _2^{\rm{s}}(N_{{\rm{r}},2}^{\rm{s}} + b_{{\rm{r}},2}^{\rm{s}} - b_2^{\rm{s}}) + c(d_{{\text{I}}{{\text{F}}_{12}}}^{\rm{s}} - d_{{\rm{r}}{\text{,I}}{{\text{F}}_{12}}}^{\rm{s}}) \end{array} \right..$$ (9) 2. 实验数据及处理策略
为了检验DCB和OSB产品在双频IF模型中的应用,本次实验选取50个MGEX测站采集的10 d的观测数据,分别进行GPS、GLONASS、Galileo以及BDS四个系统的实验. 观测数据的采样间隔为30 s,所有测站均能接收到各GNSS的基准频率,测站的地理位置分布图如图1所示.
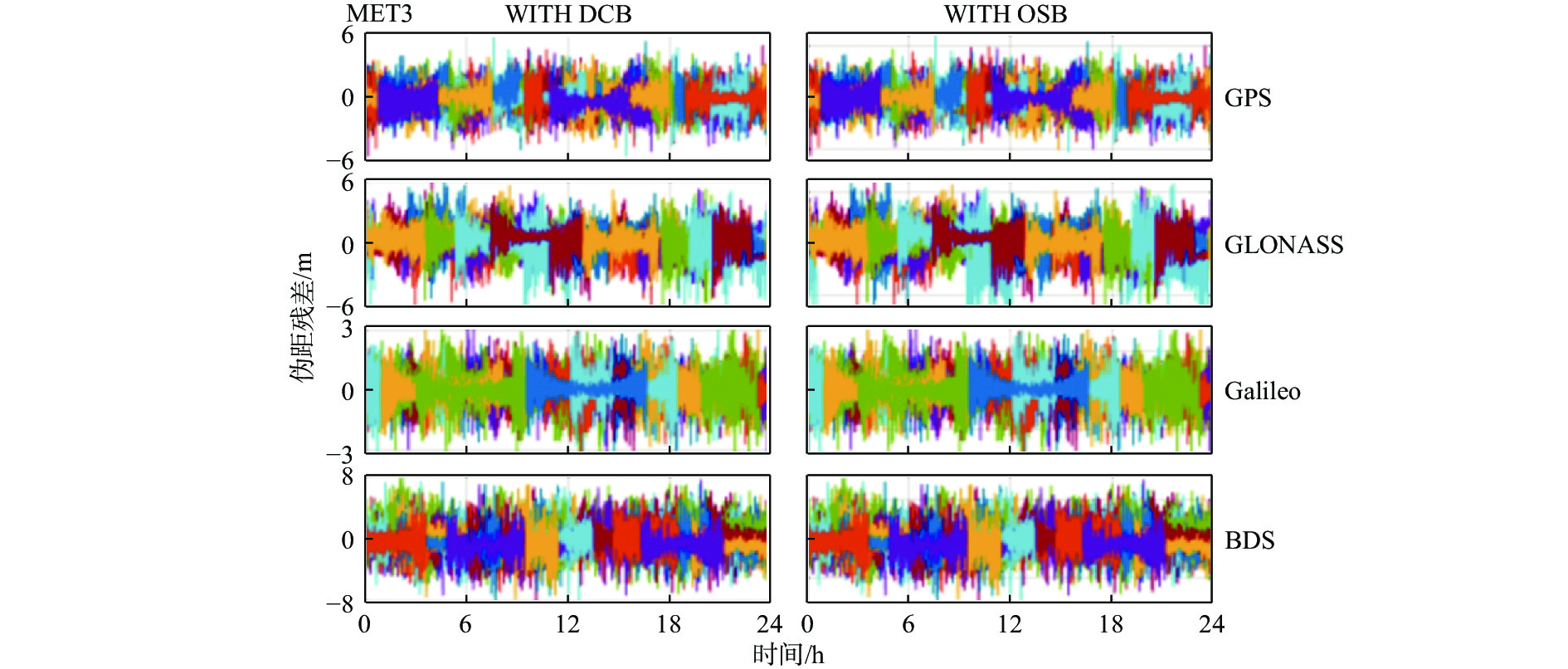
表1总结了DCB和OSB两种产品的实验策略,不同之处在于对卫星伪距偏差的改正. 其中卫星和接收机的天线改正采用IGS发布的atx文件[12],对于缺少的Galileo和BDS接收机天线改正,采用相应的GPS第一、二频代替. 以IGS中心提供的SINEX文件中坐标为坐标真值,当测站的东(E)、北(N)、天顶(U)三个方向的绝对定位误差连续60个历元(30 min)均小于0.1 m时判定为收敛[13]. 由于观测残差包括测量噪声和建模误差,因此,可以通过输出的观测残差是否遵循零均值高斯分布来评估PPP模型,同时检测模型误差是否完全改正. 图2表示采用两种不同产品策略时,MET3测站上IF模型计算的各GNSS的伪距残差分布,不同的颜色表示不同的卫星. 可以看出无论是采用传统的DCB产品还是采用OSB产品改正伪距偏差,各GNSS的伪距残差均在0值附近,初步说明DCB和OSB产品在改正伪距偏差上的一致性和正确性.
表 1 实验处理策略项目 改正模型或处理策略 PPP模型 双频IF组合模型 观测值 GPS: L1/L2; GLONASS: G1/G2; Galileo: E1/E5a; BDS: B1I/B3I 采样间隔 30 s 卫星截止高度角 10° 精密星历 GBM产品 卫星伪距硬件延迟改正 采用CAS发布的后缀名为DCB和OSB的文件 卫星或接收机天线改正 igs14.atx文件 地球自转 模型改正 相对论效应 模型改正 天线相位缠绕 模型改正 地球潮汐 模型改正 地球自转 模型改正 测站位置 静态PPP采用常数估计 接收机钟差 采用白噪声估计 对流层延迟 干延迟采用萨斯塔莫宁模型计算;传播路径上的湿延迟投影至U方向作为参数进行随机游走估计 模糊度 采用常数估计 3. 实验结果和分析
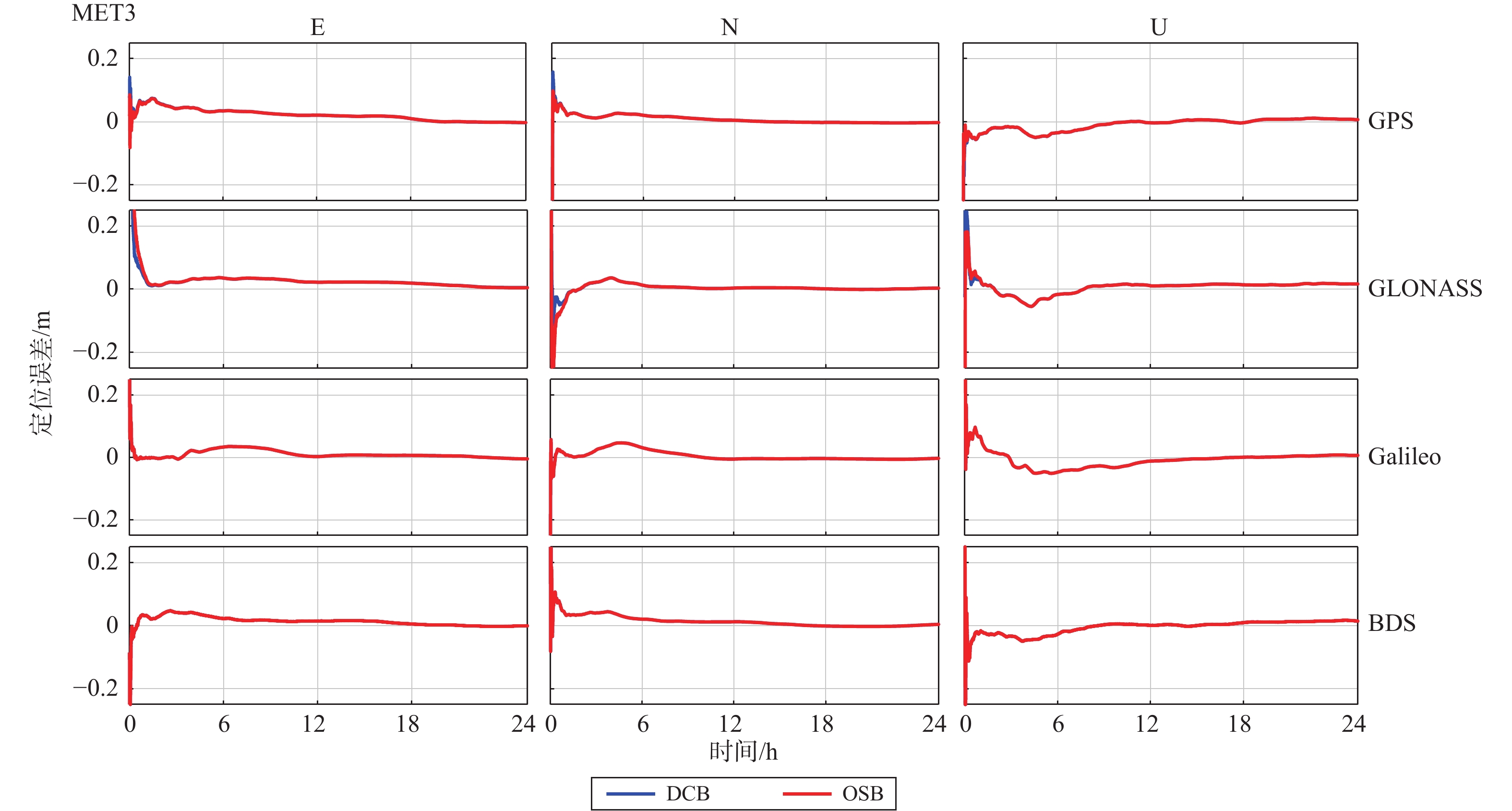
本文分别用CAS发布的DCB和OSB产品进行四种方案的双频IF实验:GPS、GLONASS、Galileo以及BDS,并以定位精度的均方根误差(RMSE)和收敛时间来评定PPP模型的性能. 图3显示采用不同产品时,MET3测站在年积日第182天的四种方案PPP模型静态定位误差曲线图,蓝色和红色曲线分别表示采用DCB产品和OSB产品. 可以看出,无论是用DCB产品还是OSB产品,各方案的定位误差曲线几乎重合.
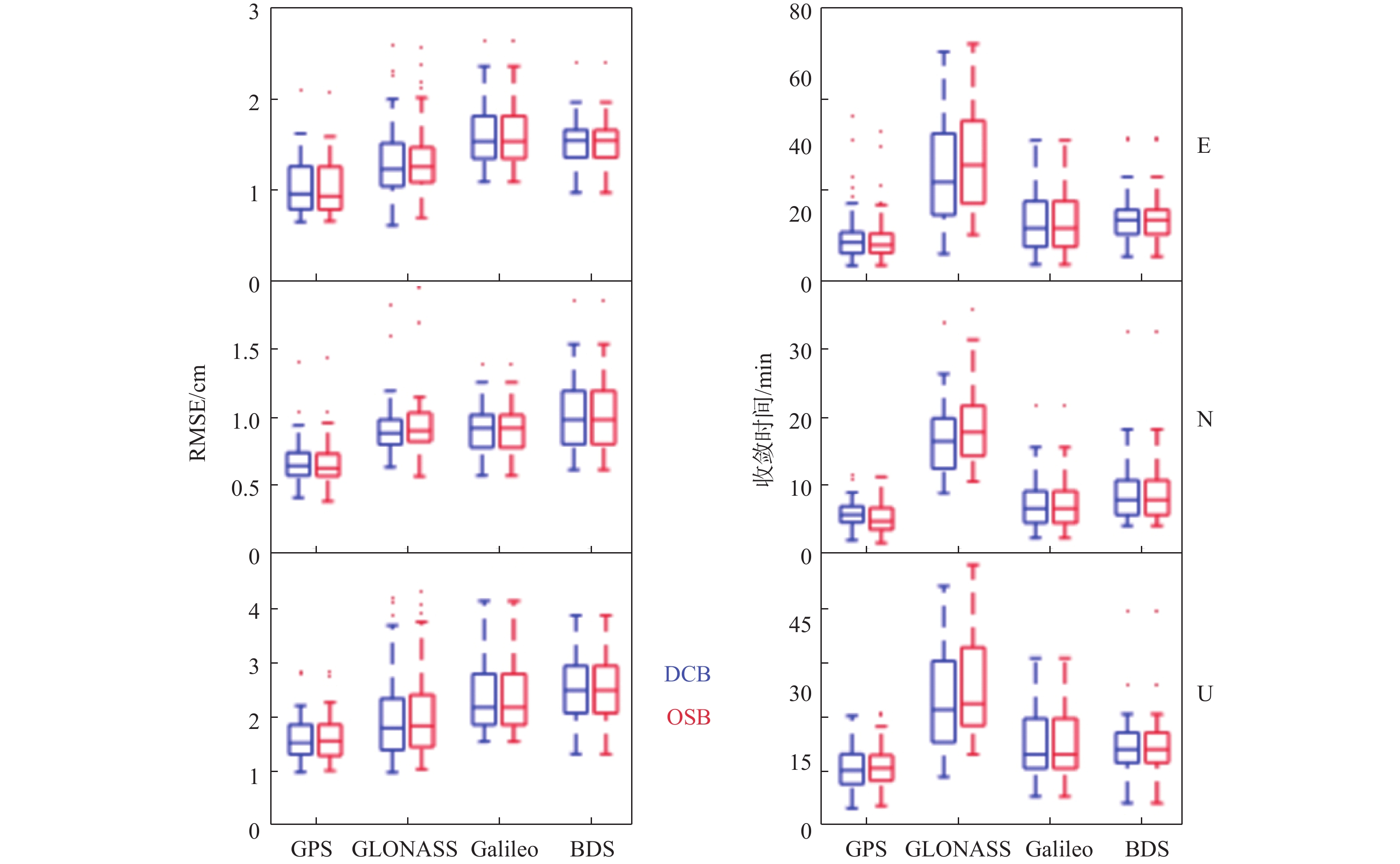
为了进一步科学全面地对比分析两种产品对PPP模型的影响,本文统计了50个MGEX测站10 d平均的三维收敛时间和RMSE值,如图4所示. 由于实验选取的测站分布范围广,表2阐明了收敛时间和RMSE值的中位数. 由表2和图4可知,DCB和OSB两种产品对GPS和GLONASS方案的定位性能略有差别但差异不大,对Galileo和BDS方案的效果是一样的. 采用OSB产品时,GPS方案的定位性能最好,三维定位精度能达到0.92 cm、0.63 cm、1.57 cm,总收敛时间为15.50 min;GLONASS方案的定位精度比GPS稍微差点,但是收敛时间是四个方案中最差的,为38.08 min;Galileo方案的定位性能与BDS在同一水平内,但比BDS方案略好;得益于卫星数的提升,BDS方案在23.10 min时即可达到收敛,收敛后的三维定位精度为1.53 cm、0.98 cm和2.50 cm.
表 2 不同产品方案下三维定位RMSE值和收敛时间统计表系统 RMSE/cm E N U 收敛时间/min DCB OSB DCB OSB DCB OSB DCB OSB GPS 0.94 0.92 0.65 0.63 1.54 1.57 16.33 15.50 GLONASS 1.22 1.24 0.89 0.92 1.81 1.85 37.73 38.08 Galileo 1.52 1.52 0.92 0.92 2.19 2.19 24.80 24.80 BDS 1.53 1.53 0.98 0.98 2.50 2.50 23.10 23.10 4. 结 论
为了应对未来多频多模的PPP技术,本文在原始观测方程的基础上,分别推导出适用于CAS发布的DCB产品和OSB产品的双频IF模型,并采用50个MGEX测站观测的10 d数据分别对不同的方案验证模型的可用性,即GPS、GLONASS、Galileo、BDS四种方案.
实验结果表明,DCB和OSB两种产品下GPS或GLONASS方案的定位精度差异可以忽略不计;使用OSB产品能一定程度上减少GPS方案的收敛时间,但是却稍微延长了GLONASS方案的收敛效果,这可能与GLONASS系统的频分多址(FDMA)信号调制方法有关. 此外,两种产品下Galileo和BDS方案的定位性能是一样的. 综合使用方法和对各系统的定位影响,以后PPP模型的处理策略中,完全可以采用OSB产品代替传统的DCB产品. 采用OSB产品时,GPS方案的定位性能最好,三维定位精度能达到0.92 cm、0.63 cm、1.57 cm,总收敛时间为15.50 min;GLONASS方案的定位精度比GPS稍微差点,但是收敛时间是四个方案中最差的;Galileo方案的定位性能与BDS在同一水平内,但比BDS方案略好.
本文对OSB产品的研究仅限于伪距层面,并没有涉及到相位OSB产品在模糊度固定方面的应用. 因此在后续的研究中,我们将侧重于相位OSB产品的生成策略及模糊度固定方面的应用.
-
表 1 实验处理策略
项目 改正模型或处理策略 PPP模型 双频IF组合模型 观测值 GPS: L1/L2; GLONASS: G1/G2; Galileo: E1/E5a; BDS: B1I/B3I 采样间隔 30 s 卫星截止高度角 10° 精密星历 GBM产品 卫星伪距硬件延迟改正 采用CAS发布的后缀名为DCB和OSB的文件 卫星或接收机天线改正 igs14.atx文件 地球自转 模型改正 相对论效应 模型改正 天线相位缠绕 模型改正 地球潮汐 模型改正 地球自转 模型改正 测站位置 静态PPP采用常数估计 接收机钟差 采用白噪声估计 对流层延迟 干延迟采用萨斯塔莫宁模型计算;传播路径上的湿延迟投影至U方向作为参数进行随机游走估计 模糊度 采用常数估计 表 2 不同产品方案下三维定位RMSE值和收敛时间统计表
系统 RMSE/cm E N U 收敛时间/min DCB OSB DCB OSB DCB OSB DCB OSB GPS 0.94 0.92 0.65 0.63 1.54 1.57 16.33 15.50 GLONASS 1.22 1.24 0.89 0.92 1.81 1.85 37.73 38.08 Galileo 1.52 1.52 0.92 0.92 2.19 2.19 24.80 24.80 BDS 1.53 1.53 0.98 0.98 2.50 2.50 23.10 23.10 -
[1] YANG Y X, LI J L, XU J Y, et al. Contribution of the compass satellite navigation system to global PNT users[J]. Chinese science bulletin, 2011, 56(26): 2813-2819. DOI: 10.1007/S11434-011-4627-4
[2] 朱少林, 岳东杰, 何丽娜, 等. BDS-2/BDS-3融合三频精密单点定位模型及偏差特性分析[J/OL]. (2021-11-05)[2022-04-22]. 武汉大学学报(信息科学版), 2021(11): 1-15. [3] WU Z Y, WANG Q X, YU Z H, et al. Modeling and performance assessment of precise point positioning with multi-frequency GNSS signals[J]. Measurement, 2022, 201(30): 111687.
[4] WANG N B, YUAN Y B, LI Z S, et al. Determination of differential code biases with multi-GNSS observations[J]. Journal of geodesy, 2015, 90(3): 209-228. DOI: 10.1007/s00190-015-0867-4
[5] WU Z Y, WANG Q X, HU C, et al. Modeling and assessment of five-frequency BDS precise point positioning[J]. Satellite navigation, 2022, 3(1): 114-127,10004. DOI: 10.1186/S43020-022-00069-Z
[6] SCHARE S. SINEX BIAS-Solution (Software/technique) Independent exchange format for GNSS biases version 1.00[S]. IGS Workshop on GNSS biases, Bern, Switzerland, 2016. https://files.igs.org/pub/data/format/sinex_bias_100.pdf
[7] ALFRED L, LEV R, DMITRY T. GPS Satellite Surveying[M]. 4th Edition. 2015.
[8] 魏子卿, 刘光明, 吴富梅. 2000中国大地坐标系: 中国大陆速度场[J]. 测绘学报, 2011, 40(4): 403-410. [9] HU C, WANG Q X, WU Z Y, et al. A mixed multi-frequency precise point positioning strategy based on the combination of BDS-3 and GNSS multi-frequency observations[J]. Measurement science and technology, 2022, 34(2): 25008. DOI: 10.1088/1361-6501/ac9a62
[10] LIU G, GUO F, WANG J, et al. Triple-frequency GPS un-differenced and uncombined PPP ambiguity resolution using observable-specific satellite signal biases[J]. Remote sensing, 2020, 12(14): 2310. DOI: 10.3390/rs12142310
[11] 李昕. 多频率多星座GNSS快速精密定位关键技术研究[D]. 武汉: 武汉大学, 2021. [12] 吴志远, 王潜心, 胡超, 等. BDS-3多频PPP模型性能分析[J]. 大地测量与地球动力学, 2022, 42(8): 846-851. DOI: 10.14075/j.jgg.2022.08.014 -
期刊类型引用(1)
1. 李怡文,赵子雯,陈姬君,梁亚茹,魏凯,王棣星,李敏. 北斗三号新频点绝对信号码偏差性能对比评估. 全球定位系统. 2024(06): 14-24+83 .  本站查看
本站查看
其他类型引用(0)


















































 下载:
下载: