The effects of higher order ionosphere on GNSS tropospheric parameters estimation
-
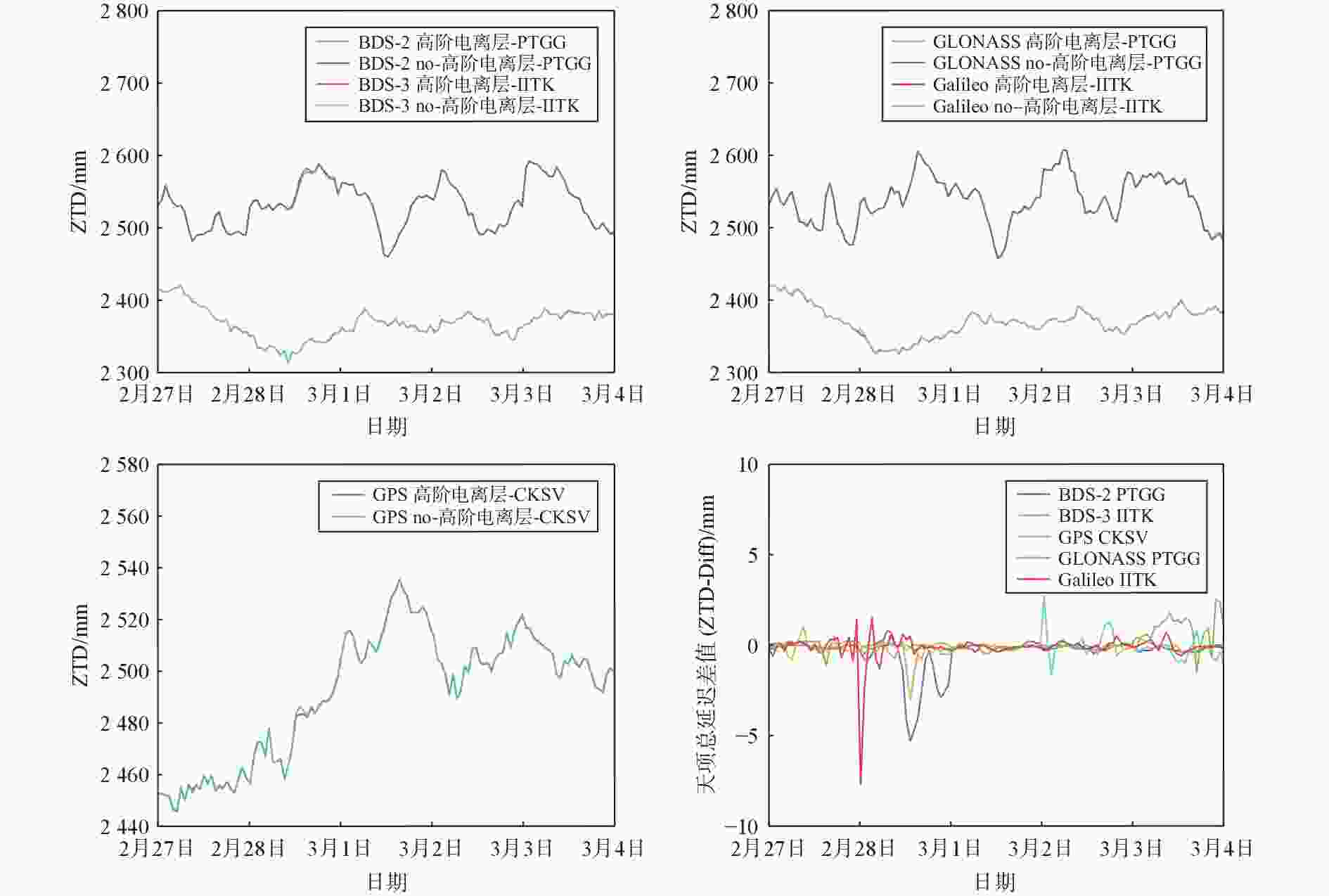
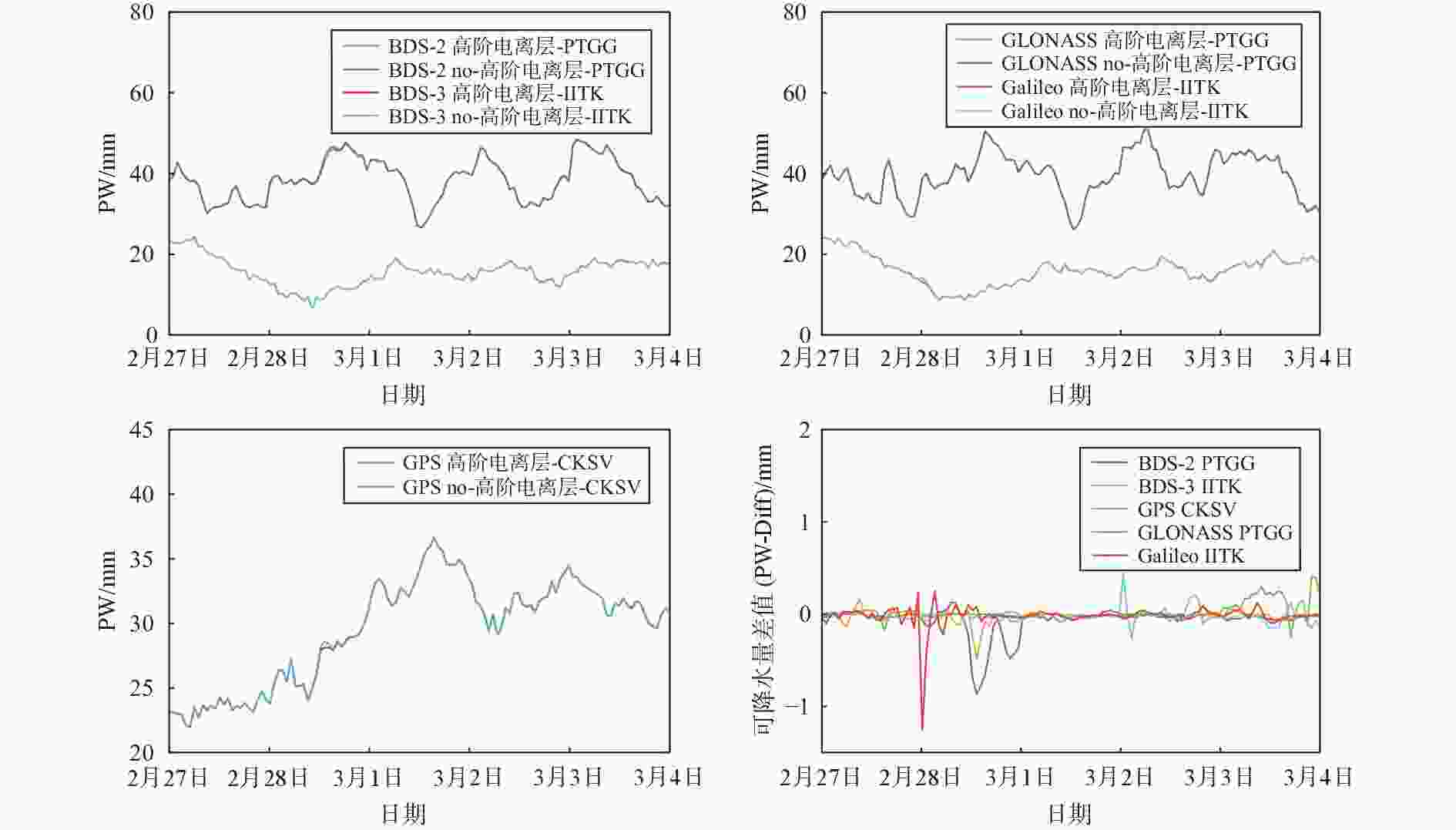
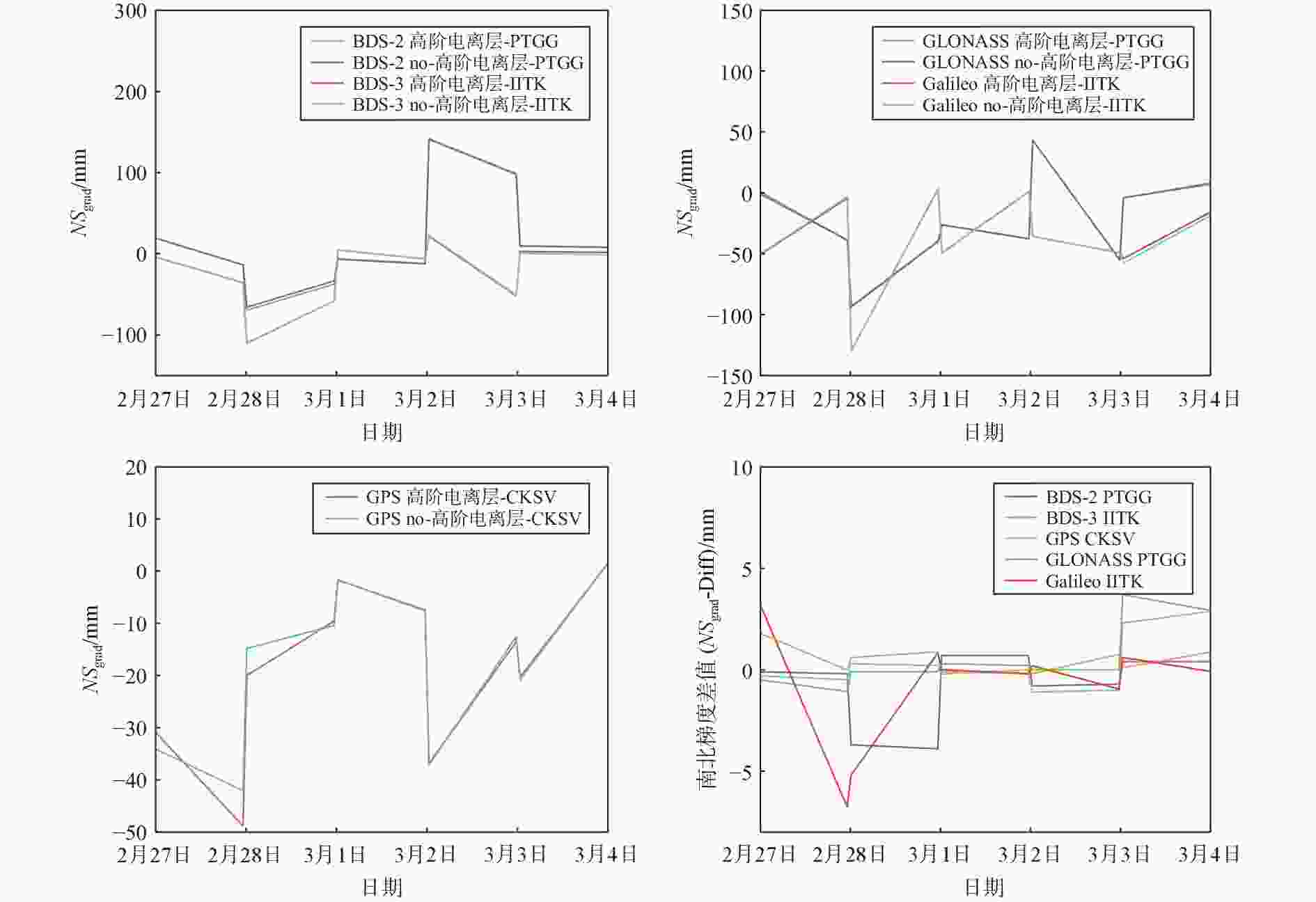
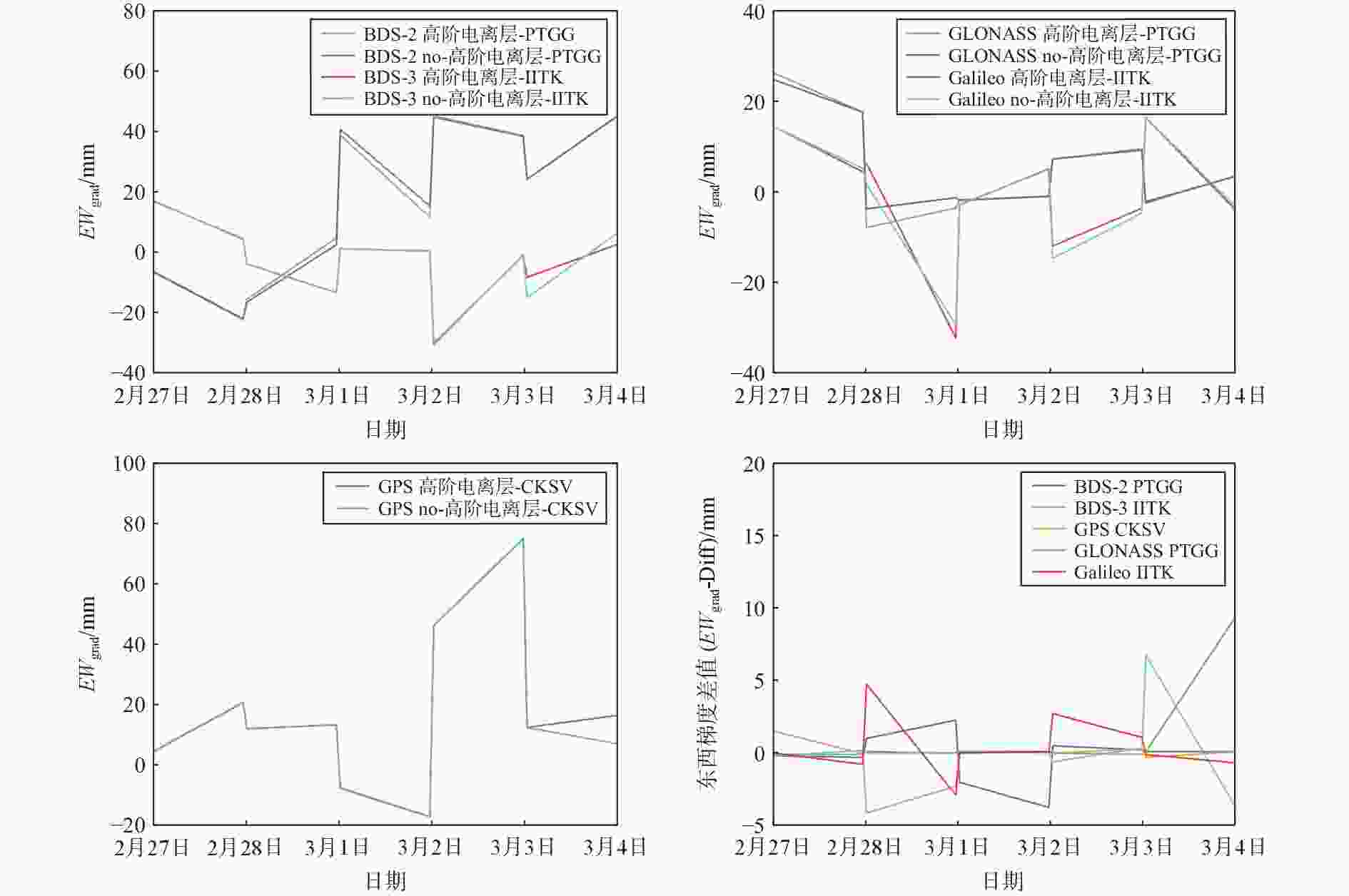
摘要: 为了研究高阶电离层在全球卫星导航系统(GNSS)对流层参数估计中的影响. 在太阳活动平静期和活跃期,分别选择亚太地区的8个MGEX (Multi-GNSS Experiment)跟踪站. 通过GAMIT10.71分析了高阶电离层延迟在北斗二号(BDS-2)、北斗三号(BDS-3)、GPS、GLONASS和Galileo对流层参数估计的影响. 实验结果表明:太阳活动平静期,高阶电离层延迟对于Galileo的对流层天顶总延迟(ZTD)、可降水量(PW)和南北梯度(
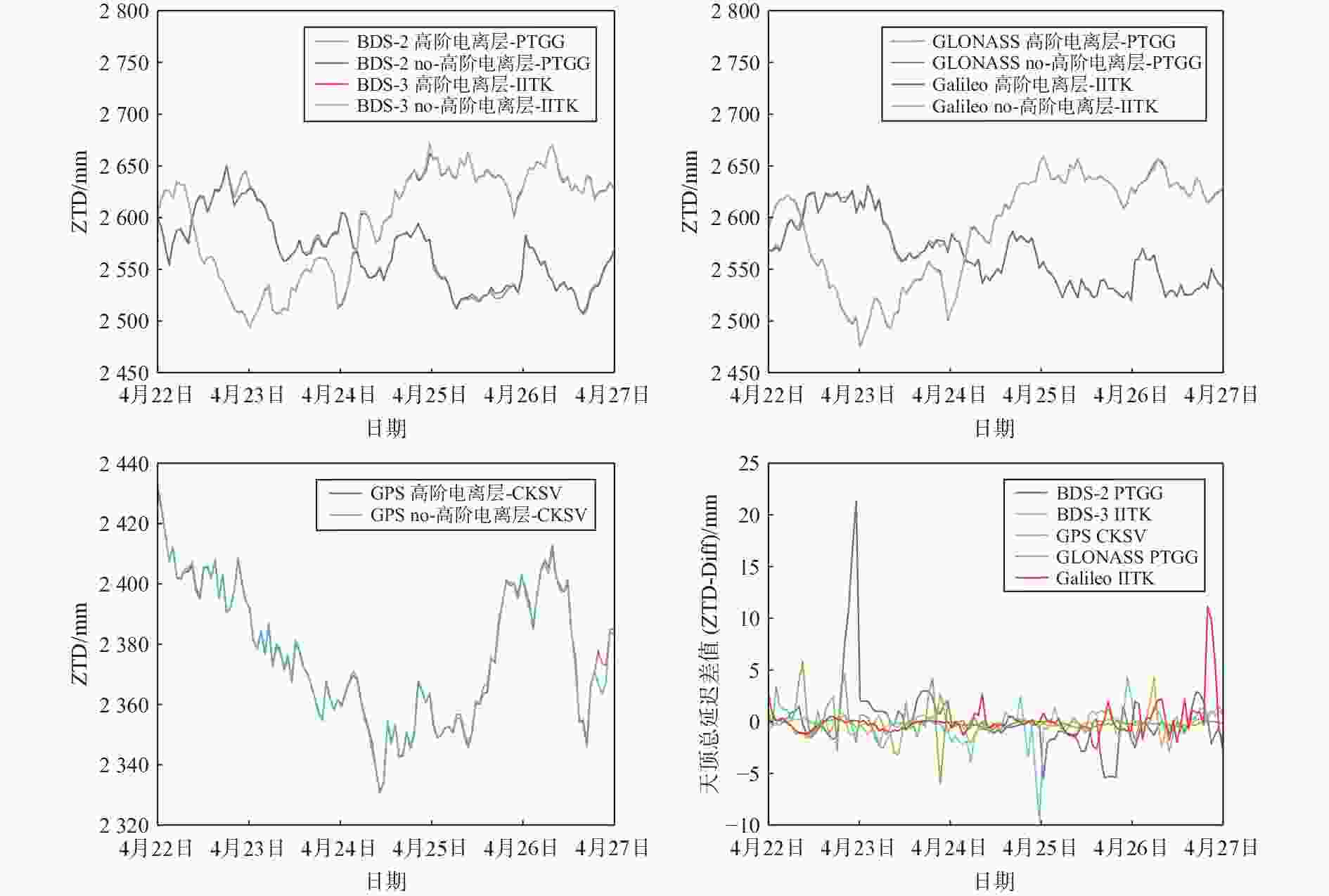
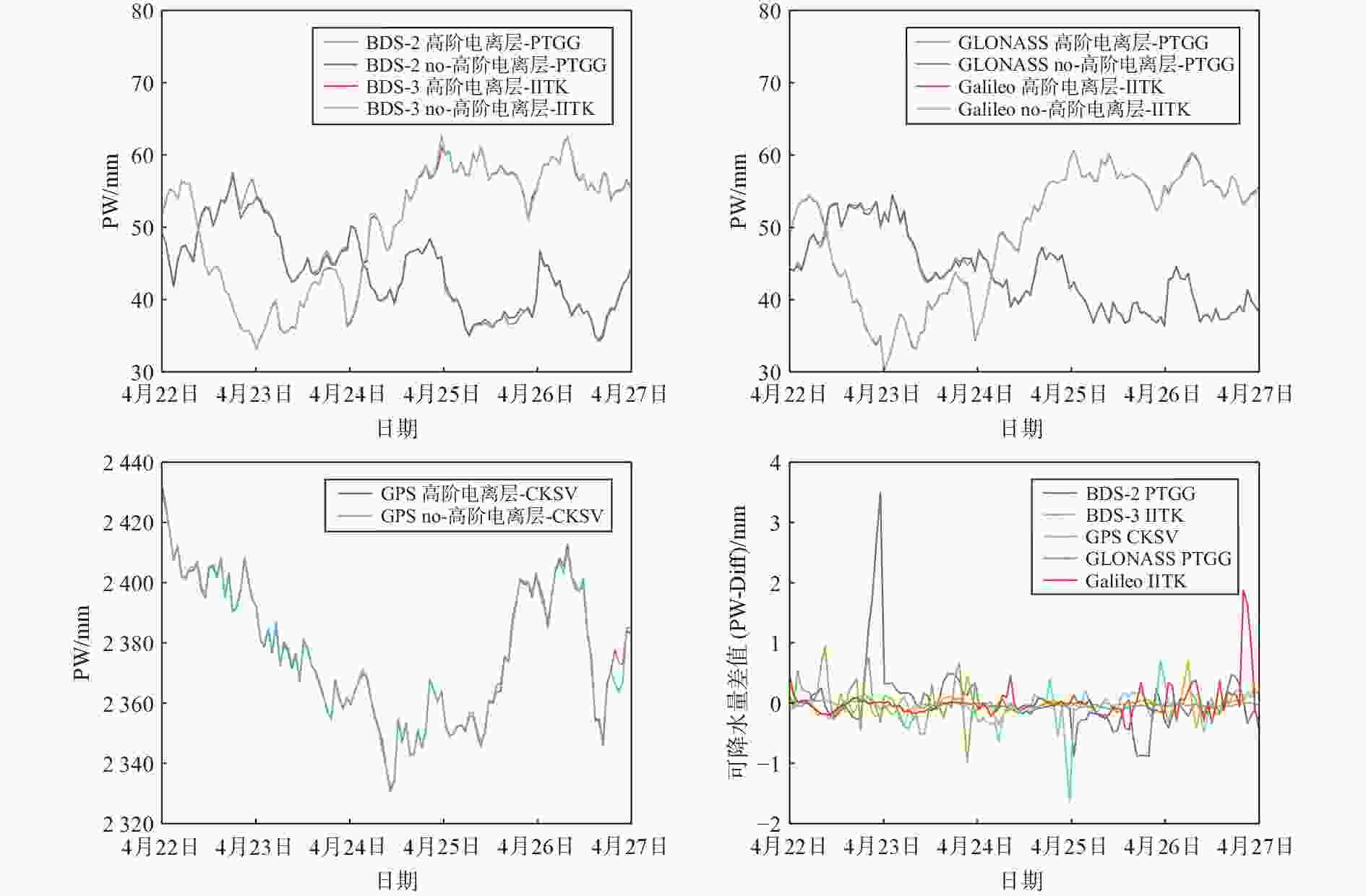
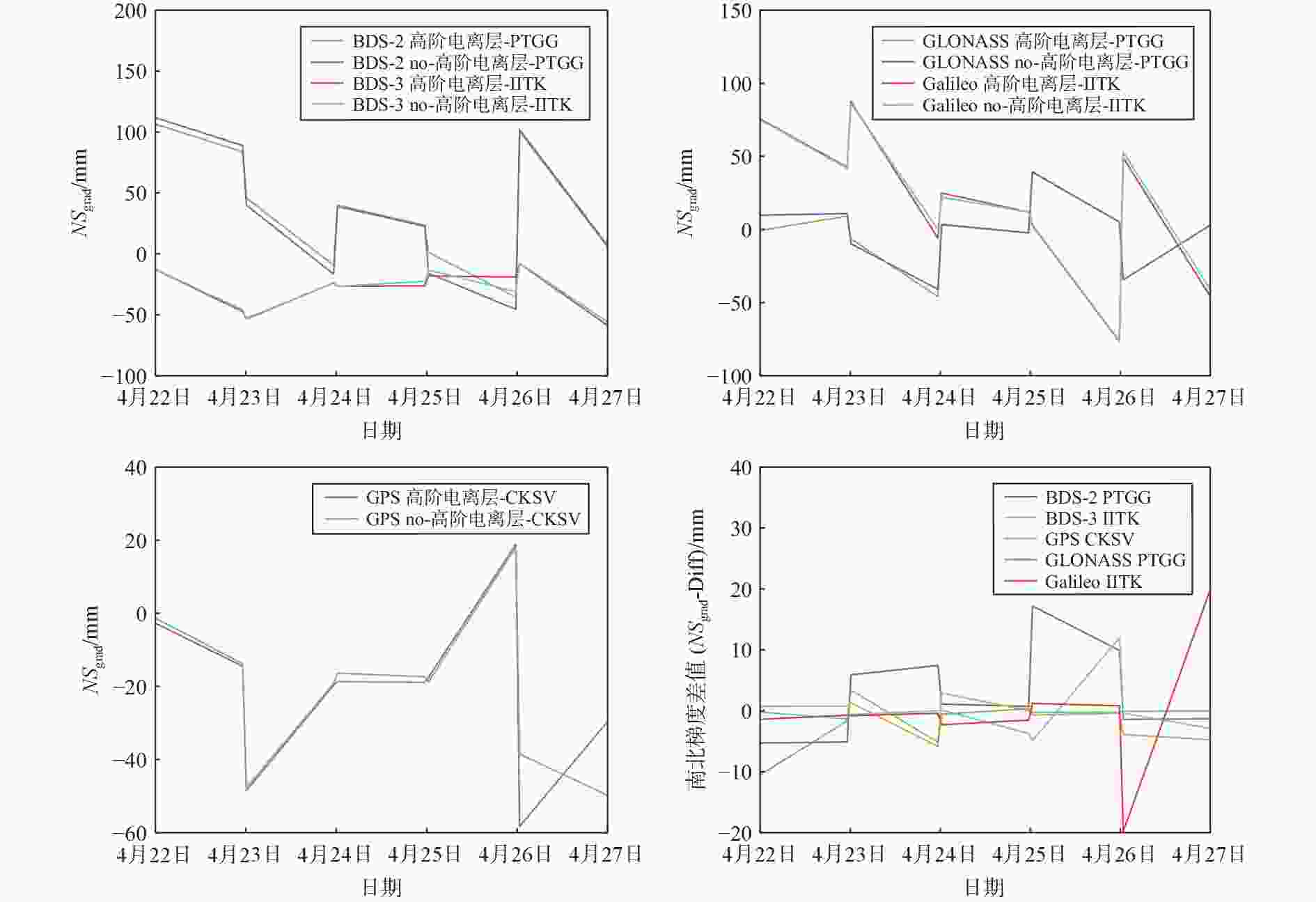
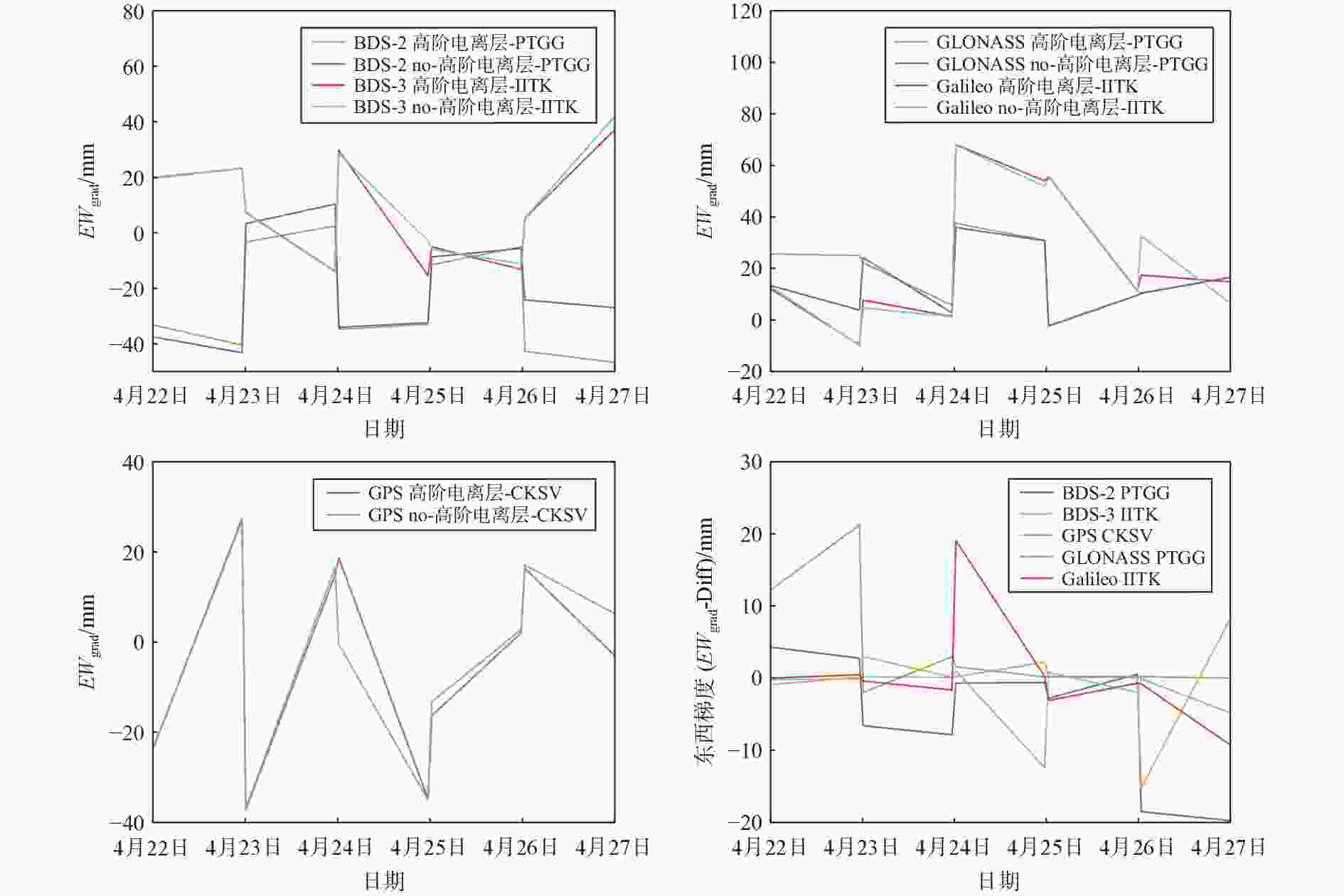
${{NS}}_{\text{grad}}$ )影响最大分别达到7.70 mm、1.26 mm和6.77 mm;高阶电离层延迟对于GLONASS的对流层东西梯度(${{EW}}_{\text{grad}}$ )影响最大达到9.30 mm. 太阳活动活跃期,高阶电离层在GNSS对流层参数估计中产生了更大影响. 其中,高阶电离层延迟对于BDS-2的ZTD和PW影响最大分别达到21.30 mm和3.49 mm;高阶电离层延迟对于Galileo的对流层${{NS}}_{\text{grad}}$ 影响最大达到19.87 mm;高阶电离层延迟对于GLONASS的对流层${{EW}}_{\text{grad}}$ 影响最大达到了21.21 mm. 实验结果进一步表明:高阶电离层在GNSS对流层PW估计的影响较小;ZTD、${{NS}}_{\text{grad}}$ 和${{EW}}_{\text{grad}}$ 影响则较大. 高阶电离层延迟对于BDS-3和GPS对流层参数估计影响较小;Galileo、BDS-2和GLONASS影响则较大.-
关键词:
- 高阶电离层延迟 /
- 全球卫星导航系统(GNSS) /
- 太阳活动平静期 /
- 太阳活动活跃期 /
- 对流层参数估计
Abstract: In order to study the influence of the high-order ionosphere on the Global Navigation Satellite System (GNSS) tropospheric parameter estimation eight MGEX (Multi GNSS Experience) tracking stations in the Asia Pacific region were selected during the quiet and active periods of solar activity The influence of high-order ionosphere delay on tropospheric parameter estimation in Beidou-2 Navigation Satellite System (BDS-2), Beidou-3 Navigation Satellite System (BDS-3), Global Positioning System (GPS), Global Navigation Satellite System (GLONASS) and Galileo is analyzed through GAMIT10.71 The experimental results show that during the quiet period of solar activity, the maximum influence of high-order ionosphere delay on Galileo’s zenith total delay (ZTD), precipitable water (PW) and north south gradient (${{NS}}_{\text{grad}}$ ) is 7.70 mm, 1.26 mm and 6.77 mm respectively; The maximum effect of high-order ionosphere delay on the tropospheric east west gradient (${{EW}}_{\text{grad}}$ ) of GLONASS is 9.30 mm during the active solar period, high-order ionosphere has greater influence on the tropospheric parameter estimation of GNSS among them, the maximum impact of high-order ionosphere delay on the tropospheric ZTD and PW of BDS-2 is 21.30 mm and 3.49 mm respectively; The maximum influence of high-order ionosphere delay on the tropospheric${{NS}}_{\text{grad}}$ of Galileo is 19.87 mm; The maximum effect of high-order ionosphere delay on tropospheric${{EW}}_{\text{grad}}$ of GLONASS is 21.21 mm The experimental results further show that high-order ionosphere has little influence on the tropospheric PW estimation of GNSS; ZTD,${{NS}}_{\text{grad}}$ and${{EW}}_{\text{grad}}$ have greater influence high-order ionosphere delay has little effect on BDS-3 and GPS tropospheric parameter estimation; Galileo, BDS-2 and GLONASS have greater influence -
表 1 GAMIT10. 71基线解算策略和配置文件
参数 解算方式 文件名称 文件内容 观测值类型 LC_AUTCLN antmod. dat 接收机天线信息 解算策略 BASELINE atml. grid 全球大气负荷参数格网模型 观测量 LC_AUTCLN dcb. dat 接收机码间偏差 迭代方案 1-ITER gdetic. dat 地球形状参数 高度截止角 10° leap. sec 跳秒表 采样间隔 30 s luntab. 月球星历文件 卫星钟差
模型精密星历误差的钟差参数 map. grid 全球大气映射函数模型 对流层模型 SAAS模型 nutabl. 章动 对流层参数输出间隔 1 h rcvant. dat 接收机及天线型号对照表 光压模型 ECOMC模型 otl. grid 全球海潮模型 天体延迟
参数13 otlcmc. dat 海洋潮汐负荷
改正梯度参数 2 pole. usno 极移 先验坐标所属框架 ITRF2014 sestbl. 解算参数控制 惯性框架 J2000 svnva. dat 卫星星号对照 测站约束 0.02 m/0.02 m/0.02 m process. defaults 处理控制 表 2 太阳活动平静期状况
日期 射电流量
10.7 cm太阳黑子数 X射线背景 耀斑 质子流量(GOES13)
大于10 MeV Protons /
(cm2-day-sr)电子流量(GOES13)
大于2 MeV Electrons /
(cm2-day-sr)地磁Ap指数 X射线耀斑 光学耀斑 C M X S 1 2 3 2022-02-27 97 48 B1.5 1 0 0 1 0 0 0 4.30×104 5.30×106 13 2022-02-28 99 65 B1.7 3 0 0 2 0 0 0 4.30×104 1.80×106 8 2022-03-01 99 62 B2.2 0 0 0 2 0 0 0 4.30×104 2.70×106 8 2022-03-02 110 66 B3.7 7 1 0 5 1 0 0 4.30×104 3.10×106 4 2022-03-03 111 92 B3.2 3 0 0 1 0 0 0 4.30×104 5.50×106 5 表 3 ZTD差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 0.27 0.45 0.20 0.31 0.23 0.43 0.16 0.35 0.30 0.40 GAMG 0.17 0.24 0.14 0.20 0.10 0.14 0.09 0.12 0.12 0.19 IITK 0.41 0.81 0.27 0.45 0.96 0.19 0.13 0.19 0.31 0.81 JFNG 0.25 0.33 0.16 0.22 1.20 0.13 0.11 0.15 0.19 0.30 MIZU 0.16 0.20 0.19 0.28 1.21 0.14 0.14 0.29 0.15 0.23 PTGG 0.46 1.03 0.23 0.38 1.04 0.20 0.31 0.58 0.27 0.39 ULAB 0.22 0.55 0.13 0.20 1.17 0.15 0.10 0.13 0.14 0.21 URUM 0.27 0.61 0.17 0.24 1.02 0.10 0.11 0.14 0.21 0.57 表 4 PW差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 0.04 0.07 0.03 0.05 0.04 0.07 0.03 0.06 0.05 0.06 GAMG 0.03 0.04 0.02 0.03 0.02 0.02 0.01 0.02 0.02 0.03 IITK 0.07 0.13 0.04 0.07 0.03 0.04 0.02 0.03 0.05 0.13 JFNG 0.04 0.05 0.02 0.03 0.02 0.03 0.02 0.02 0.03 0.05 MIZU 0.02 0.03 0.03 0.04 0.02 0.03 0.02 0.50 0.02 0.04 PTGG 0.08 0.17 0.04 0.06 0.03 0.05 0.05 0.10 0.04 0.07 ULAB 0.03 0.08 0.02 0.03 0.02 0.04 0.01 0.02 0.02 0.03 URUM 0.04 0.09 0.03 0.04 0.02 0.02 0.02 0.02 0.03 0.09 表 5 NSgrad差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 0.74 0.95 0.71 1.07 0.16 0.22 0.23 0.44 0.69 0.84 GAMG 0.36 0.46 0.17 0.30 0.23 0.31 0.14 0.23 0.23 0.35 IITK 0.53 0.77 0.59 1.24 0.17 0.26 0.24 0.37 1.20 2.03 JFNG 0.43 0.50 0.40 0.59 0.20 0.25 0.31 0.51 0.28 0.36 MIZU 0.33 0.42 0.20 0.35 0.32 0.55 0.13 0.20 0.39 0.63 PTGG 1.16 1.77 0.89 1.27 0.51 0.65 0.89 1.54 1.44 1.90 ULAB 0.38 0.82 0.31 0.49 0.38 0.66 0.04 0.06 0.42 0.74 URUM 0.34 0.49 0.22 0.37 0.10 0.14 0.15 0.20 0.64 1.36 表 6 EWgrad差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 1.04 1.51 0.67 1.56 0.86 1.50 0.36 0.68 0.96 1.43 GAMG 0.33 0.53 0.22 0.41 0.21 0.27 0.17 0.24 0.22 0.27 IITK 0.51 0.74 0.68 1.47 0.27 0.41 0.18 0.34 0.42 0.56 JFNG 0.60 1.02 0.12 0.22 0.18 0.23 0.21 0.27 0.56 1.06 MIZU 0.42 0.57 0.54 0.90 0.50 0.63 0.39 0.53 0.28 0.31 PTGG 0.67 0.98 0.46 0.70 0.37 0.47 1.00 2.44 0.88 1.49 ULAB 0.30 0.39 0.23 0.39 0.21 0.34 0.12 0.16 0.22 0.31 URUM 0.28 0.39 0.27 0.41 0.12 0.16 0.16 0.19 0.30 0.41 表 7 太阳活动活跃期情况
日期 射电流量
10.7 cm太阳黑子数 X射线背景 耀斑 质子流量(GOES13)
大于10 MeV Protons /
(cm2-day-sr)电子流量(GOES13)
大于2 MeV Electrons /
(cm2-day-sr)地磁Ap指数 X射线耀斑 光学耀斑 C M X S 1 2 3 2022-04-22 163 101 B8.0 7 2 0 2 0 1 0 4.00×104 9.00×106 7 2022-04-23 160 118 B8.1 8 0 0 5 0 0 0 3.90×104 1.10×107 13 2022-04-24 159 112 B7.6 3 0 0 2 0 0 0 3.80×104 8.90×106 5 2022-04-25 157 94 B8.0 8 2 0 7 0 0 0 3.80×104 1.20×107 5 2022-04-26 150 126 B9.4 7 0 0 3 0 0 0 3.80×104 1.40×107 3 表 8 ZTD差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 1.67 3.23 0.64 0.94 0.51 0.88 0.88 1.45 0.91 1.20 GAMG 0.60 0.82 0.51 0.69 0.25 0.32 0.35 0.53 0.54 0.89 IITK 0.90 1.18 0.59 1.03 0.38 0.54 0.40 0.59 0.87 1.71 JFNG 0.87 1.14 0.52 0.67 0.48 0.72 0.49 0.72 0.71 1.12 MIZU 0.54 0.67 0.80 1.09 0.24 0.30 0.29 0.39 0.65 0.92 PTGG 1.93 3.08 0.83 1.46 0.58 0.84 0.36 0.49 0.81 1.35 ULAB 0.72 0.90 0.46 0.59 0.29 0.37 0.31 0.43 0.62 0.88 URUM 0.83 1.08 0.38 0.54 0.24 0.32 0.24 0.31 0.65 1.05 表 9 PW差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 0.27 0.53 0.10 0.15 0.08 0.14 0.14 0.24 0.15 0.20 GAMG 0.09 0.13 0.08 0.11 0.04 0.05 0.06 0.08 0.08 0.14 IITK 0.15 0.20 0.10 0.17 0.06 0.09 0.07 0.10 0.15 0.29 JFNG 0.14 0.19 0.08 0.11 0.08 0.12 0.80 0.12 0.11 0.18 MIZU 0.09 0.11 0.13 0.17 0.04 0.05 0.05 0.06 0.10 0.15 PTGG 0.32 0.51 0.13 0.24 0.10 0.14 0.06 0.08 0.13 0.22 ULAB 0.11 0.14 0.07 0.09 0.04 0.06 0.05 0.07 0.10 0.14 URUM 0.13 0.17 0.06 0.09 0.04 0.05 0.04 0.05 0.10 0.17 表 10 NSgrad差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 2.57 3.89 1.29 1.80 1.35 1.71 1.79 3.21 2.57 3.69 GAMG 1.46 1.91 0.68 0.85 0.29 0.38 0.74 1.11 0.78 1.07 IITK 2.91 3.47 1.21 1.44 0.86 1.15 0.75 1.00 2.99 5.46 JFNG 1.43 1.73 0.97 1.16 0.93 1.19 1.15 1.60 2.52 3.36 MIZU 1.05 1.39 1.93 3.07 0.31 0.44 0.62 0.91 0.91 1.26 PTGG 5.54 7.25 2.58 3.03 1.93 2.56 1.40 2.42 1.80 2.60 ULAB 2.42 3.27 0.69 0.94 0.42 0.52 0.41 0.55 2.30 2.90 URUM 2.84 3.81 0.65 0.89 0.26 0.34 0.31 0.47 0.92 1,81 表 11 EWgrad差值绝对值的Mean和RMS
m MGEX跟踪站 BDS-2 BDS-3 GPS GLONASS Galileo Mean RMS Mean RMS Mean RMS Mean RMS Mean RMS CKSV 1.54 1.87 2.19 2.84 0.87 1.12 3.84 7.62 2.46 3.17 GAMG 2.47 3.79 1.05 1.60 0.40 0.52 0.52 0.65 0.77 0.98 IITK 3.36 3.90 2.29 3.17 0.73 0.88 0.51 0.57 2.52 5.07 JFNG 6.35 9.31 1.32 2.10 0.85 1.00 0.72 1.32 3.57 5.70 MIZU 1.72 2.58 1.89 3.40 0.79 0.99 0.68 0.88 2.73 3.89 PTGG 6.60 8.39 2.23 3.02 1.99 3.66 0.94 1.56 2.95 4.03 ULAB 2.72 3.49 0.94 1.31 0.53 0.71 0.40 0.58 1.26 1.48 URUM 3.79 4.43 0.87 1.09 0.32 0.36 0.19 0.23 1.14 2.09 -
[1] TREGONING P, BOERS R, O’BRIEN D, et al. Accuracy of absolute precipitable water vapor estimates from GPS observations[J]. Journal of geophysical research atmospheres, 1998, 103(D22): 28701-28710. DOI: 10.1029/98JD02516 [2] BÖHM J, NIELL A E, TREGONING P, et al. Global mapping function(GMF): a new empirical mapping function based on numerical weather model data[J]. Geophysical research letters, 2006, 33(7): 304-316. DOI: 10.1029/2005GL025546 [3] SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin géodésique, 1972, 46(3): 279-298. DOI: 10.1007/BF02521844 [4] HOPFIELD H S. Tropospheric effect on electromagnetically measured range: prediction from surface weather data[J]. Radio science, 1971, 6(3): 357-367. DOI: 10.1029/RS006i003p00357 [5] KLOBUCHAR J A. Ionospheric effects on GPS[J]. American institute of aeronautics and astronautics, 1996(1): 485-515. DOI: 10.2514/5.9781600866388.0485.0515 [6] HOQUE M M, JAKOWSKI N. Estimate of higher order ionospheric errors in GNSS positioning[J]. Radio science, 2008, 43(5): 68-82. DOI: 10.1029/2007rs003817 [7] ELMAS Z G, AQUNINO M, MARQUES H A, et al. Higher order ionospheric effects in GNSS positioning in the european region[J]. Annales geophysicae, 2011, 29(8): 1383-1399. DOI: 10.5194/angeo-29-1383-2011 [8] WANG Z M, WU Y, ZHANG K F, et al. Triple-frequency method for high-order ionospheric refractive error modelling in GPS modernization[J/OL]. [2022-08-20]. Journal of global positioning systems, 2005, 4(1-2): 291-295. https://www.scirp.org/journal/PaperInformation.aspx?paperID=324 [9] BRUNNER F K, GU M. An improved model for the dual frequency ionospheric correction of GPS observations[J]. Manusur geod, 1991(16): 205-214. [10] BASSIRI S, HAJJ G A. Higher-order ionospheric effects on the global positioning system observables and means of modelling them[J]. Manuscripta geodaetica, 1993, 18(5): 280-289. [11] PETRIE E J, KING M A, MOORE P, et al. Higher-order ionospheric effects on the GPS reference frame and velocities[J]. Journal of geophysical research:solid earth, 2010, 115(B3): B03417. DOI: 10.1029/2009JB006677 [12] FRITSCHE M, DIETRICH R, KNOFEL C, et al, Impact of higher-order ionospheric terms on GPS estimates[J]. Geophysical research letters, 2005, 32(23): 23311. DOI: 10.1029/2005GL024342 [13] GARCIA-FERNANDEZ M, DESAI S D, BUTALA M D, et al. Evaluation of different approaches to modeling the second-order ionospheric delay on GPS measurements[J]. Journal of geophysical research:space physics, 2013, 118(12): 7864-7873. DOI: 10.1002/2013JA019356 [14] ELSOBEIEY M, EL-RABBANY A. Impact of second-order ionospheric delay on GPS precise point positioning[J/OL]. [2022-08-20]. Journal of applied geodesy, 2011, 5(1): 37-45. https://www.zhangqiaokeyan.com/academic-journal-foreign_journal-applied-geodesy_thesis/0204112329466.html [15] HERNANDEZ-PAJARES M, JUAN J M, SANZ J, et al. Second-order ionospheric term in GPS: implementation and impact on geodetic estimates[J]. Journal of geophysical research:solid earth, 2007, 112(B8): B08417. DOI: 10.1029/2006JB004707 [16] AKGUL V, JIN S, GURBUZ G, et al. High-order ionospheric effects on 3-D GPS coordinate estimation in Turkey[C]//IGARSS 2018-2018 IEEE Inrenational Geoscience and Remote Sensing Symposium, 2018: 3135-3138. [17] CHEN X, GE M, MARQUES H A, et al. Evaluating the impact of higher-order ionospheric corrections on multi-GNSS ultra-rapid orbit determination[J]. Journal of geodesy, 2019, 93(9): 1347-1365. DOI: 10.1007/s00190-019-01249-7 [18] AKGUL V, GURBUZ G, KUTOGLU S H, et al. Effects of the high-order ionospheric delay on GPS-based tropospheric parameter estimations in Turkey[J]. Remote sensing, 2020, 12(21): 3569. DOI: 10.3390/rs12213569 [19] QI L, GUO J, XIA Y, et al. Effect of higher-order ionospheric delay on precise orbit determination of GRACE-FO based on satellite-borne GPS technique[J]. IEEE access, 2021(9): 29842-29849. DOI: 10.1109/ACCESS.2021.3059296 [20] ZHOU H T, WANG L, FU W J, et al. Impact of higher-order ionospheric delay on the reliability of RTK ambiguity estimation[J]. Advances in space research, 2022, 69(1): 727-736. DOI: 10.1016/j.asr.2021.09.031 [21] HADAS T, KRYPIAK-GREGORCZY A, HERNANDEZ-PAJARES M, et al. Impact and implementation of higher-order ionospheric effects on precise GNSS applications[J]. Journal of geophysical research:solid earth, 2017, 122(11): 9420-9436. DOI: 10.1002/2017jb014750 [22] ZUS F, DENG Z, WICKERT J. The impact of higher-order ionospheric effects on estimated tropospheric parameters in precise point positioning[J]. Radio science, 2017, 52(8): 963-971. DOI: 10.1002/2017rs006254 [23] 曹炳强, 成英燕, 许长辉, 等. 间距分区法在解算卫星连续运行站数据中的应用[J]. 测绘通报, 2016(11): 15-17. DOI: 10.13474/j.cnki.11-2246.2016.0355 -








 下载:
下载: