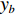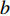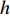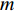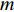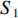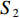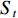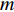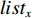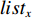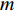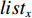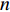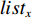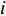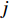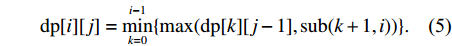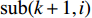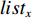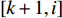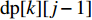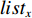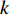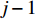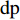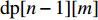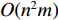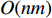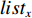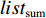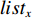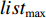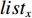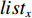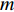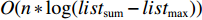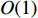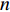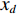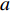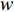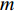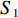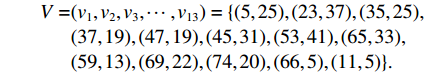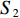UAV track planning algorithm in concave polygonal area based on remote sensing mission
-
摘要: 针对遥感观测的需求与特点,提出一种基于遥感任务的凹多边形区域无人机 (UAV) 航迹规划算法,旨在保证UAV不相撞与区域全覆盖的前提下,总耗时更短. 根据遥感影像获取的特点,采用统一主飞行方向,定点拍摄进行UAV航迹规划. 通过航线分割点求取、多边形划分、UAV分配、碎片多边形合并与UAV再分配以及航点信息求取五个步骤,得到在选定主飞行方向的情况下UAV航迹的优化. 通过选取凹多边形及其凸包的边所在的方向分别为主方向,得到全局最优解. 实验结果表明:该算法能合理分配UAV并进行航迹规划,比传统方法更为高效、适用性更强.Abstract: For the needs and characteristics of remote sensing observing. We proposes an unmanned aerial vehicle (UAV) track planning algorithm based on remote sensing tasks in concave polygonal areas. The algorithm aims to ensure UAV’s non-collision and full area coverage with shorter total time consumption. According to remote sensing image acquisition characteristics, the UAV track planning is carried out by unified main flight direction and fixed-point shooting. The UAV track optimization under the selected main flight direction is obtained through five steps: route segmentation point calculation, polygon division, UAVs assignment, fragment polygon merging and UAVs reassignment, and waypoint information calculation. The global optimal solution is obtained by selecting the main direction of the edges of the concave polygon and its convex hull, respectively. The experimental results show that the algorithm can reasonably assign UAVs and carry out track planning, which is more efficient and more applicable than traditional methods.
-
0. 引 言
由于无人机 (UAV) 具有灵活、高效的特点,不仅在遥感监测、自然灾害救援与评估等方面备受青睐,而且可以快速获取所需地区的遥感影像,以便进行监督与决策. 在UAV航迹规划领域,单机航迹规划算法已相对成熟,根据获取影像区域的特点可分为凸多边形区域单机航迹规划与凹多边形区域单机航迹规划. 对于凸多边形区域单机航迹规划算法,陈海等[1]从理论上获取了在理想情况下的飞行方案,证明当UAV的主飞行方向采用凸多边形最小宽度所在边的方向时,UAV的转弯次数最小,从而其总路程最短. COOMBES等[2]考虑了风速对UAV航迹的影响,用实验证明在风速较大的情况下,垂直于风速飞行总时间最短. 对于凹多边形区域而言,王自亮等[3]提出了基于扫描线的UAV航迹规划算法,并利用之字形策略实现了区域的全覆盖.
对于单机而言,其获取一定区域的影像往往时间较长,在处理自然灾害救援等紧急任务时,采用多机联合方案则显得尤为重要. 对于多机联合方案,目前的算法思路是将其分解为两个子问题来分别求解,即飞行区域划分优化与UAV全覆盖航迹优化[4-7]. 由于这两个子问题是分别进行优化的,所以每个飞行区域中的UAV主飞行方向并不完全相同,在野外实验时,由于存在极端环境,这种方法会存在UAV在飞行过程中相撞的风险. 对于基于遥感任务的航迹规划而言,飞行区域选在郊区是常见的现象,这些区域会受到比较严重的风速干扰,UAV可能会发生偏航现象,采用不同区域不同主飞行方向将增大UAV相撞的风险;而且在进行航迹规划设计时,UAV的转弯轨迹没有被较好地考虑,不同类型的UAV往往会采取不同的转弯策略,主方向不统一会增大UAV相撞的风险. 此外,对于遥感任务而言,其航迹飞行需要获取到航拍影像,后期还需要将这些影像拼接成图,但目前的算法方案各个区域是独立的,不同区域之间缺少重叠度,无法满足遥感成图的需求. 再者,目前的航迹规划方案都是采用定时拍摄影像,即相机每隔一定的时间进行拍摄,不需要给出具体的拍摄地点,因此不需要获取相应的航拍点位,但是由于UAV自身或者气候因素,UAV可能会发生偏航,采用这种方式获得的遥感影像质量往往较差,满足不了成图需求. 对于目前的多机航迹规划算法,它们大多适用于其他目的,并不适用于遥感成图. 如迪杰斯拉特算法(Dijkstra)及其相应改进算法[8]适用于侦查或打击任务,快速搜索随机树(RRT)及其相应改进算法[9-10]适用于火灾扑救及UAV避障,蚁群算法以及相应改进算法[11-13]适用于点对点的路径规划及侦查,
$ {\mathrm{A}}^{\mathrm{*}} $ 及其改进算法适用于点对点的路径规划以及跨区域间的搜索[14-15]. 它们无法很好地获取待观测区域的全覆盖影像,并且所获取的影像航带间的联系性不强,图像拼接较为困难,无法得到高质量的遥感影像图.综上,目前的航迹规划算法仍不能很好地适用于遥感任务中,缺少对成图需求、UAV飞行情况与特殊情况的考虑,算法鲁棒性与成图效果不尽人意. 因此本文提出基于遥感任务的凹多边区域UAV航迹规划算法,利用多机协同来进行规划,采用统一的主飞行方向、定点拍摄来进行成图,考虑遥感影像成图所需的重叠度. 在满足拍摄影像全覆盖的前提下,使得飞行任务整体时间最短.
1. 基于遥感任务的UAV航迹规划算法
基于遥感任务的UAV航迹规划算法的最终目的是获得满足需求空间分辨率的高质量遥感影像,为了解耦合航迹规划与图像拼接过程,可将图像拼接的需求浓缩为空间分辨率、航向重叠度与旁向重叠度三个指标.
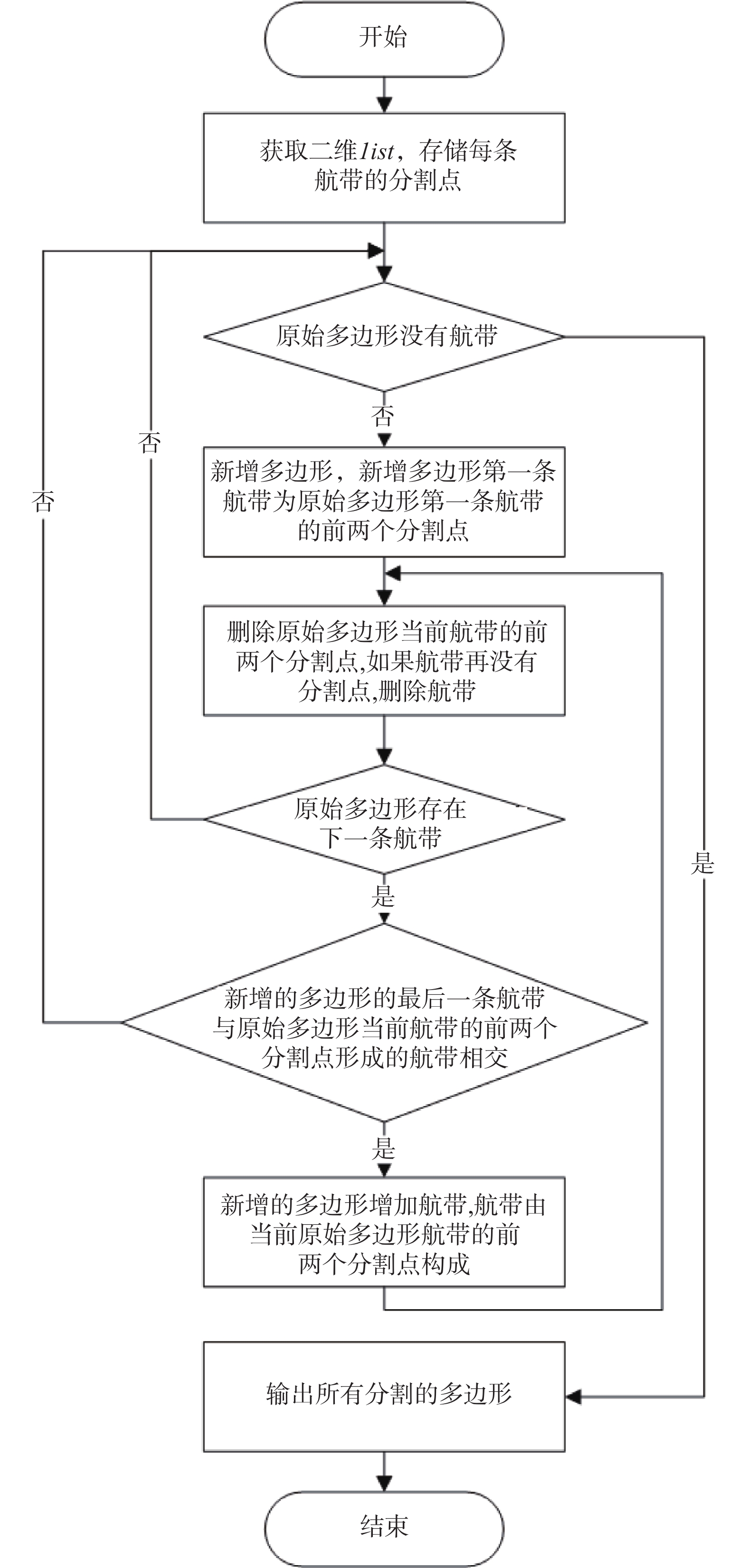
对于空间分辨率,它是指影像中的长度对应到实际地面时的比值,它与UAV的飞行高度相关,计算公式为
$$ m = \frac{f}{H}\text{.} $$ (1) 式中:
$m$ 为空间分辨率;$f$ 为相机焦距;$H$ 为UAV飞行高度.对于航向重叠度,它是指沿着UAV飞行方向两影像间的重叠度,而旁向重叠度则是指垂直UAV飞行方向两影像间的重叠度. 重叠度的计算公式如下:
$$ a = 1 - \frac{{{x_d}}}{{{w_g}}} \text{,} $$ (2) $$ b = 1 - \frac{{{y_d}}}{{{h_g}}} \text{.} $$ (3) 式中:
$a$ 为航向重叠度;$b$ 为旁向重叠度;${x_d}$ 为航向航点间隔;${y_d}$ 为旁向航点间隔;${w_g}$ 与${h_g}$ 为每张拍摄影像对应到地面实际的长度和宽度.为了获得高质量的遥感影像,需要对影像进行定点拍摄,获取到精确的定位. 如果采用定时拍摄,当受到周边环境或自身因素影响,UAV并不能到合适的点位采集到数据,造成图像拼接质量的不稳定. 在遥感任务的规划中,利用影像的大小、影像空间分辨率、影像间的重叠度可以得到每张影像对应到地面的大小、航向航点间隔与旁向航点的间隔. 为了提高算法的鲁棒性,考虑到UAV转弯等实际飞行情况与UAV偏航等特殊情况,本次算法采用统一的主飞行方向进行航迹规划,尽可能避免UAV之间发生碰撞. 考虑到算法的通用性,此算法利用多机协同来解决凹多边区域航迹规划,凸多边形区域是凹多边形区域的一种特殊情形.
因此,本次算法可描述如下:在给定遥感图像大小
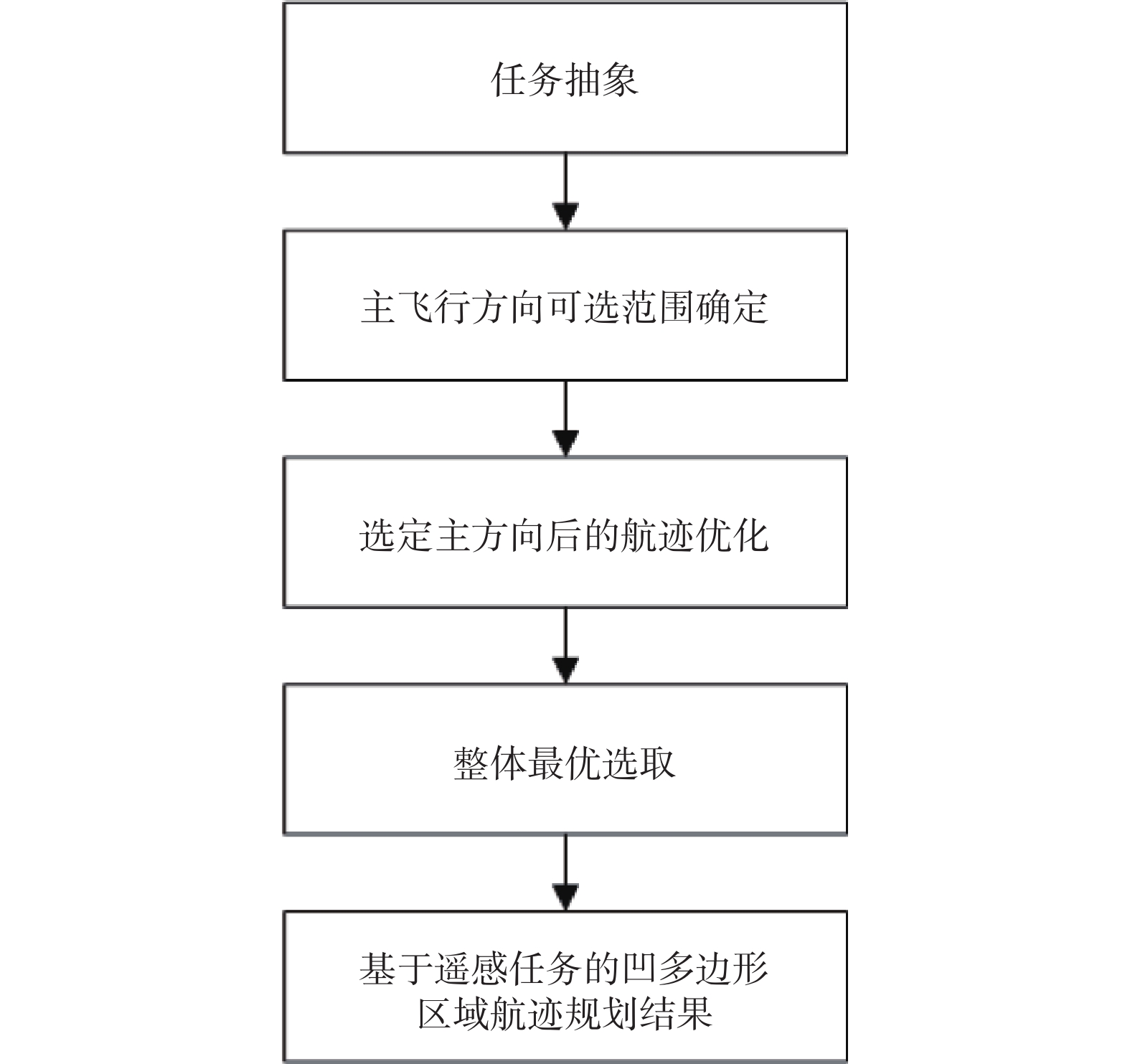
$w*h$ 、空间分辨率$s$ 、航向重叠度$a$ 、旁向重叠度$b$ 的前提下,令$m$ 架性能相同的UAV载有同一焦距$f$ 的相机去一待观测的凹多边形区域${{\rm{S}}}$ 执行遥感观测任务,如何进行UAV航迹规划设计,使得任务的总体时间最短,忽略从机场到飞行起始点的耗时,约束条件为所有UAV的主飞行方向相同. 因此本次算法主要分为两部分,一个是UAV主飞行方向的选取,另一个是选取某一主方向后,航迹规划的设计. 为了便于理解,本文将先进行第二部分的介绍,再进行主飞行方向选取的讨论,技术路线如图1所示.2. 给定主飞行方向的航迹优化模型
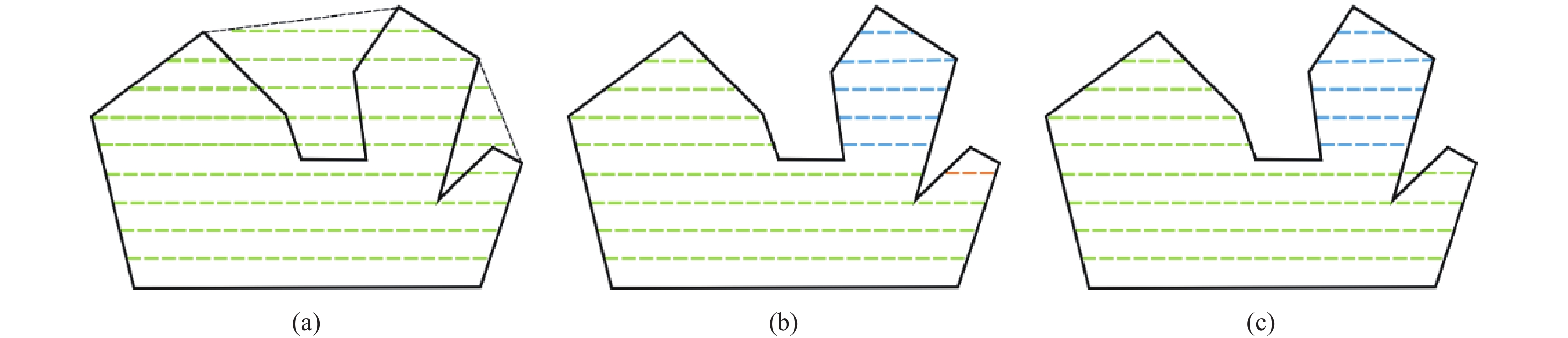
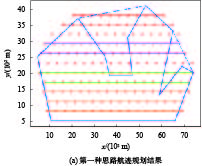
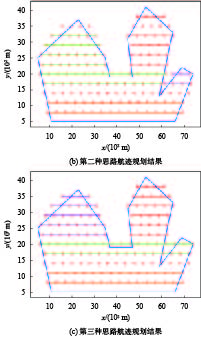
本节将讨论给定UAV的主飞行方向后的航迹优化. 对于凹多边形区域而言,给定主飞行方向后有三种可能的思路,如图2所示. 第一种思路是求取凹多边形的最小凸包,将凹多边形转换为凸多边形来进行航迹规划,如图2(a)所示. 该方法虽然简单有效,但是存在很多无效的航线,算法整体效率不高. 第二种是利用扫描线算法来对凹多边形进行划分,分割出多个区域,进而进行航迹规划,如图2(b)所示. 这种方法消除了无效的航线,极大地提升了航线的利用率,但是会存在分割的碎片区域过多问题,额外派UAV去执行飞行任务将花费较大的代价. 第三种思路是对图2中的碎片多边形进行适当合并,从而使UAV分配更为合理并提高算法效率,如图2(c)所示. 本次算法将采用第三种思路进行,整体算法依次可分解为五个部分,即航线分割点求取、多边形划分、UAV分配、碎片多边形合并与UAV再分配以及航点信息求取.
2.1 航线分割点求取
对于航线求取而言,需要获取航带间的旁向间隔,其计算公式为
$$ {y_b} = (1 - b)\frac{h}{m} . $$ (4) 式中:
${y_b}$ 为航带间的旁向间隔;$b$ 为旁向重叠度;$h$ 为影像垂直于UAV飞行方向的长度;$m$ 为空间分辨率.知晓主飞行方向与航带间的旁向间隔后可以获取航线的空间分布,获取航线的分割点仍有两种思路. 第一种是通过航线与待观测区域求交点获得;另一种是通过航带多边形与待观测区域求交,得到相交多边形在沿着航向方向上的两个端点值. 对于第一种方案,存在遗漏区域、过度分割、获取的边界图像质量较差等问题. 因此本次算法采用方案二进行.
2.2 多边形划分
对于多边形划分,将采用顺序扫描法与堆栈处理进行,利用相邻条带间的连接关系来对多边形进行划分,划分示意图如图2(b)所示,算法流程如图3所示.
2.3 UAV分配
UAV的分配问题可以简单描述如下:给定UAV数量
$m$ ,给定多个多边形区域${{{S}}_1}$ ,${{{S}}_2}$ ,···,${{{S}}_t}$ ,以及每个区域中每条航带的长度,如何分配UAV,使得UAV执行飞行任务时最大飞行距离最小. 它可以拆分为两个子问题,一个从局部入手,讨论同一多边形区域内UAV的分配问题,另一个从整体入手,讨论不同多边形区域间UAV的整体分配问题. 由于需要考虑UAV转弯时花费的距离,为简单说明,可以给每条航带增加一次UAV转弯花费的距离.2.3.1 区域内UAV分配算法
区间内的UAV分配算法主要是获取分配航带的方案,使得UAV执行飞行任务时最大的飞行距离最小. 这个问题可以简化为:给定一个整数
$m$ 以及非负数组$lis{t_x}$ ,如何将$lis{t_x}$ 分成$m$ 个非空连续子数组,使得各个子数组之和的最大值最小,记$lis{t_x}$ 中元素的个数为$n$ . 解决这个问题有两种方案:一个是动态规划,另一个是二分查找与贪心策略. 对于动态规划策略来说,可以令dp[i][j]表示将$lis{t_x}$ 的前$i$ 个数分成$j$ 个非空数组时,最小的各个子数组之和的最大值. 转移方程为$$ {\rm{dp}}[i][j] = \mathop {\min }\limits_{k = 0}^{i - 1} \{ \max ({\rm{dp}}[k][j - 1],{\rm{sub}}(k + 1,i))\} . $$ (5) 式中:
${\text{sub}}(k + 1,i)$ 表示数组$lis{t_x}$ 坐标落在$[k + 1,i]$ 中所有数字的和;${\rm{dp}}[k][j - 1]$ 表示将$lis{t_x}$ 的前$k$ 个数分成$j - 1$ 个非空数组时,最小的各个子数组之和的最大值.通过递推,可以求得
${\rm{dp}}$ 表,${\rm{dp}}[n - 1][m]$ 即为最终所求的结果. 采用动态规划的时间复杂度为$O({n^2}m)$ ,空间复杂度为$O(nm)$ ,空间复杂度为动态规划数组所需的空间开销.对于二分查找与贪心策略而言,可以用二分法来查找各个子数组之和最大值的最小值,其搜索空间的上限是
$lis{t_x}$ 中所有数字的和,即$lis{t_{{\text{sum}}}}$ ,搜索下界是$lis{t_x}$ 中的最大值$lis{t_{{\text{max}}}}$ . 假定好这个最小的最大值后,可以按照贪心策略依次进行$lis{t_x}$ 的划分. 依据贪心策略划分出的$lis{t_x}$ 子数组的数量与$m$ 的关系决定二分查找的方向,直到找出最优解. 第二种策略的时间复杂度为$O(n*\log (lis{t_{{\text{sum}}}} - lis{t_{\max }}))$ ,空间复杂度为$O(1)$ . 在$n$ 比较大时,采用第二种算法性能更优,因此本次区域内无人机分配算法采用二分查找与贪心策略进行计算.2.3.2 区域间UAV的整体分配算法
区域间UAV的整体分配算法采用贪心策略以得到合适的UAV分配方案,使得在多个多边形区域中,各个UAV执行飞行任务时最大飞行距离最小. 具体而言,区域间UAV的整体分配方法可简单表述如下:给定UAV数量m,区域数量为n,将区域内总航迹长度按从小到大进行排序,组成多边形区域数组lists,每个多边形区域包含每条航带的长度信息,求对应多边形的UAV数量列表listp.
该问题的求解可以具体分成三个步骤S1、S2与S3. 对于步骤S1,可以令初始UAV数量列表listp为[1,1,···,1,m−n+1],利用区间内UAV分配算法,在每个区域lists[i]内计算当分配listp[i]架UAV时,所有UAV航程最大的最小值,将这些最小值组成数组listmax,之后转到步骤S2.
对于步骤S2,在listmax中查询最大值的下标,将其记为idmax,对应的最大值记为valuemax,若idmax为n−1,则直接返回数组listp,否则转到步骤S3.
对于步骤S3,需要在listp中寻找同时满足以下三个条件的idneed:idneed≠idmax;listp[idneed]>1;当listp[idneed]为listp[idneed]−1时,对应区域中UAV的最大航程的最小值小于valuemax. 如果不存在满足条件的idneed,则获得最终结果,直接返回数组listp;如果存在,则给listp[idneed]赋值为listp[idneed]−1,给listp[idmax]赋值为listp[idmax]+1,更新listmax,转到步骤S2继续进行循环.
最终求得的listp便是本算法所期望的结果.
2.4 碎片多边形合并与UAV再分配
对于碎片多边形的合并,主要解决问题是碎片多边形和哪个多边形合并以及合并后是否更优的问题. 由于是采用扫描线算法划分的多边形,扫描线算法很好地保持了多边形的邻近性原则,可以让碎片多边形沿主飞行方向进行合并,如图2(c)所示.
对于多边形合并是否更优问题,算法流程图如图4所示,主要分成两种情况,第一种是碎片多边形只指派一架UAV执行飞行任务,第二种是碎片多边形指派多于一架UAV的情形,第二种情况可能会融合碎片多边形的部分条带.
2.5 航点信息求取
为每架UAV分配好航线后还需要获取具体的航拍点位,航拍点位的获取依据航向拍摄间隔,其计算公式为
$$ {x_d} = (1 - a)\frac{w}{m} . $$ (6) 式中:
${x_d}$ 为航带间的航向拍摄间隔;$a$ 为航向重叠度;$w$ 为影像平行于UAV飞行方向的长度;$m$ 为实际分辨率.得到UAV的航向拍摄间隔后可以得到UAV各个航线的航点分布,可以设置UAV第一条航线的起始点都在待观测区域的同一侧.
3. UAV主飞行方向的选取
在选定主飞行方向的情况下使得UAV航迹规划最优,则可以通过选取合适的主飞行方向使得整体方案最优. 对于凸多边形区域,陈海等[5]证明主飞行方向平行于凸多边形最小宽度所对应的边时整体路径最短. 但是对于凹多边形而言,采用这种方式飞行可能会增加无效的航程,使得整体方案不能达到最优. 如图8所示,采用图8(b)的主方向飞行反而比采用图8(a)的主方向飞行更优. 通过大量实验可发现,不论是凸多边形还是凹多边形,它们的最优主方向都属于多边形及其凸包所在边的方向. 因此,猜想凹多边形区域的最优主方向属于凹多边形及其凸包所在边的方向,在第4节的实验部分将采用实验来证明其合理性. 由于计算一个主飞行方向的最优航点分布所需的时间较短,不足0.01 s,因此可以通过采用多边形及其凸包所在边的所有方向分别为UAV的主飞行方向,来寻找全局最优解.
4. 实验分析
4.1 航迹优化分析
第2节中,针对主方向选定的航迹规划有三种算法思路,本节将通过实验证明算法的优越性. 给定任务一如下所示.
观测区域
${{{S}}_1}$ ,如图5所示,共13个顶点,其顶点坐标为$$ \begin{split} V =& ({v_1},{v_2},{v_3}, \cdots ,{v_{13}}) = \{ (5,25),(23,37),(35,25), \\& (37,19),(47,19),(45,31),(53,41),(65,33), \\ &(59,13),(69,22),(74,20),(66,5),(11,5)\} . \end{split} $$ 旁向重叠度为0.5,航向重叠度为0.5,航向间隔为400 m,旁向间隔为300 m,UAV 4架,一次转弯花费500 m,UAV的飞行速度设为45 km/h.
三种思路的航迹规划结果如图6所示,图6(a)是将凹多边形区域转为凸多边形区域,进而进行UAV航迹规划. 目前在遥感领域,大多数算法都采取这种方式. 图6(b)是将凹多边形通过扫描线算法分解成多个区域,在每个区域分别分配不同的UAV去执行飞行任务. 这种方法主要存在的缺点是区域间的UAV分配不均匀,导致算法性能受到限制. 图6(c)是本文提供的算法,是在凹多边形划分算法的基础上进行优化,将部分碎片多边形区域或者其部分区域进行合并,从而得到更好的结果. 耗时与总路程结果如表1所示. 可以看到,本文提出的算法与凹多边形分割算法相比总路程虽差不多,但耗时缩短22.4%,这得益于UAV任务分配的均衡;与传统的转换到凸包的算法相比,本文提出的算法耗时缩短4.0%,总路程缩短15.0%,极大地减少了冗余航线,从而提升了算法的效率.
表 1 不同航迹规划算法的UAV耗时与总路程算法 耗时/s 总路程/km 基于凸包的UAV航迹规划算法 1 616 68.7 基于凹多边形分割的UAV航迹规划算法 2000 59.0 基于遥感任务的UAV航迹规划算法 1 552 58.4 4.2 主方向选取分析
对于凹多边形区域主方向选取问题,王自亮等[3]认为应该先求凹多边形区域的最小凸包,将凸包的最小宽度所对应边的方向选取为最优主方向,但是这种选择方式对于本文提出的算法并不适用. 考虑任务二如表2所示:
表 2 不同方向航迹规划UAV耗时与总路程方向 耗时/s 总路程/km 采用凸包最小宽度所在边的方向 2 800 69.0 全局比较方向 2 080 51.3 给定观测区域
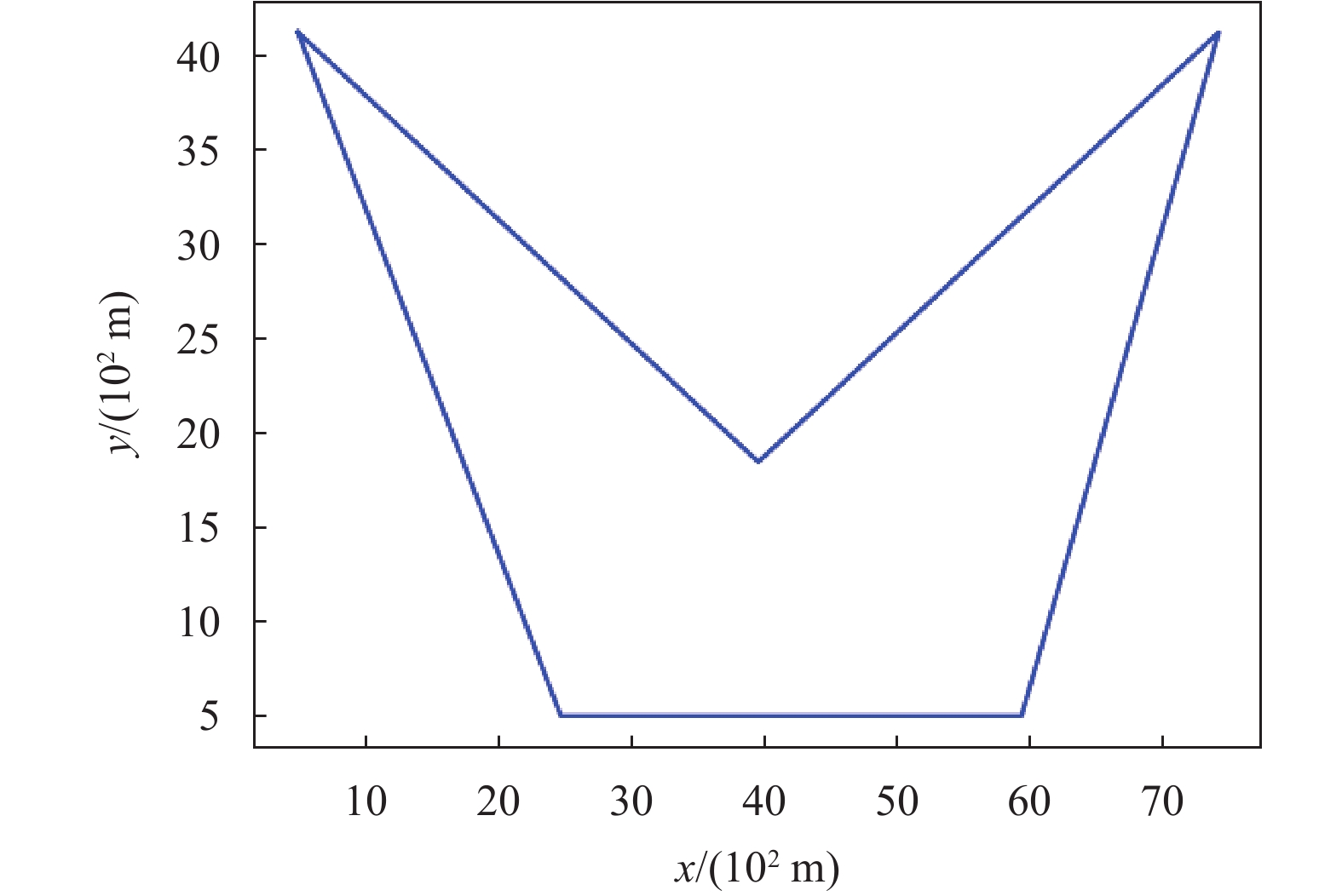
${{{S}}_2}$ ,如图7所示,共5个顶点,其顶点坐标如下
$$ \begin{split} V =& ({v_1},{v_2},{v_3},{v_4},{v_5}) \\ =& \{ (5,40),(40,18),(75,40),(60,5),(25,5)\} . \end{split} $$ 旁向重叠度为0.5,航向重叠度为0.5,航向间隔为400 m,旁向间隔为300 m,UAV2架,一次转弯花费500 m,UAV的飞行速度设为45 km/h.
图8(a)是采用凸包的最小宽度所在边的方向为主方向时进行的航迹规划方案,图8(b)是采用本文提出的全局比较得到的最优主方向进行的航迹规划方案. 表2是两种方案的耗时与总路程比较结果. 可以发现,采用全局比较得到的结果比采用凸包的最小宽度所在边的方向为主方向的结果耗时缩短25.7%,总路程缩短25.7%. 主要原因是选用凸包的最小宽度所在边的方向为主方向时,可能存在区域划分不均衡现象并导致碎片多边形进行合并,从而引起冗余距离的增加. 这种冗余距离的增加可能抵消转弯次数减小带来的收益.
对于全局比较而言,其选择的主方向范围是凹多边形及凹多边形对应凸包所在边的方向. 为了证明选择范围的合理性,将通过任务一与任务二,主飞行方向以每隔20°在[0°, 180°]范围中分别进行UAV航迹规划. 表3是各个角度的耗时与总路程比较结果,通过比较发现,采用最优方向时,UAV耗时最短、总路程最短,从而证实全局比较范围选取的合理性.
表 3 各个方向航迹规划UAV耗时与总路程方向/(°) 任务一 任务二 耗时/s 总路程/km 耗时/s 总路程/km 最优方向 1 556 58.4 2 080 51.3 0 1 556 58.4 2 800 69.0 20 1 792 62.2 2 592 61.3 40 1 598 59.6 2 384 53.3 60 1 584 58.8 2 332 55.4 80 1 664 60.8 2 304 53.6 100 1 634 60.4 2 348 52.8 120 1 720 61.3 2 146 51.4 140 1 742 61.8 2 218 51.7 160 1 858 64.7 2 512 62.4 5. 结 论
结合遥感图像拼接任务,为更高效地获取高质量影像,本文提出了基于遥感任务的凹多边形区域UAV航迹规划算法. 算法主要分为两部分,第一部分是选定主飞行方向后的UAV航迹优化,该优化方法采用扫描线算法进行多边形的划分,结合二分算法与贪心算法合并碎片多边形或碎片多边形部分区域,使得任务分配更为合理,从而提升算法效率;第二部分是主飞行方向的选取,通过实验证明最优主方向在凹多边形及其凸包的边所在的方向上,从而可以通过全局比较选择合适的主飞行方向. 本算法不仅适用于凹多边形区域,也适用于凸多边形区域,可以对指定方向进行UAV航迹规划,也适用于不同架次的UAV规划,因此有较为广泛的适用性.
但是本文只考虑了联通区域的UAV航迹规划,还缺少对非联通区域UAV航迹规划算法的研究. 对于UAV以及载荷也都是统一的,缺少多样性的考虑. 当UAV载荷的焦距不同时,每架UAV的飞行高度会存在差异,这会导致每架UAV拥有独自的航向间隔与旁向间隔,使得观测区域分配与UAV相耦合,这些也是本文后续要进一步研究的方向.
-
表 1 不同航迹规划算法的UAV耗时与总路程
算法 耗时/s 总路程/km 基于凸包的UAV航迹规划算法 1 616 68.7 基于凹多边形分割的UAV航迹规划算法 2000 59.0 基于遥感任务的UAV航迹规划算法 1 552 58.4 表 2 不同方向航迹规划UAV耗时与总路程
方向 耗时/s 总路程/km 采用凸包最小宽度所在边的方向 2 800 69.0 全局比较方向 2 080 51.3 表 3 各个方向航迹规划UAV耗时与总路程
方向/(°) 任务一 任务二 耗时/s 总路程/km 耗时/s 总路程/km 最优方向 1 556 58.4 2 080 51.3 0 1 556 58.4 2 800 69.0 20 1 792 62.2 2 592 61.3 40 1 598 59.6 2 384 53.3 60 1 584 58.8 2 332 55.4 80 1 664 60.8 2 304 53.6 100 1 634 60.4 2 348 52.8 120 1 720 61.3 2 146 51.4 140 1 742 61.8 2 218 51.7 160 1 858 64.7 2 512 62.4 -
[1] 陈海, 王新民, 焦裕松, 等. 一种凸多边形区域的无人机覆盖航迹规划算法[J]. 航空学报, 2010, 31(9): 1802-1808. [2] COOMBES M, FLETCHER T, CHEN W H, et al. Optimal polygon decomposition for UAV survey coverage path planning in wind[J]. Sensors, 2018, 18(7): 2132. DOI: 10.3390/s18072132
[3] 王自亮, 罗德林, 吴顺祥. 凹多边形区域覆盖无人机航迹规划方法[J]. 航空兵器, 2020, 26(1): 95-100. [4] 彭辉, 沈林成, 霍霄华. 多UAV协同区域覆盖搜索研究[J]. 系统仿真学报, 2007, 19(11): 2472-2476. DOI: 10.3969/j.issn.1004-731X.2007.11.022 [5] 陈海, 何开锋, 钱炜祺. 多无人机协同覆盖路径规划[J]. 航空学报, 2016, 37(3): 928-935. [6] ARAÚJO J F, SUJIT P B, SOUSA J B. Multiple UAV area decomposition and coverage[C]// IEEE Symposium on Computational Intelligence for Security and Defense Applications, 2013. DOI: 10.1109/CISDA.2013.6595424
[7] GUASTELLA D C, CANTELLI L, GIAMMELLO G, et al. Complete coverage path planning for aerial vehicle flocks deployed in outdoor environments[J]. Computers and electrical engineering, 2019(75): 189-201. DOI: 10.1016/j.compeleceng.2019.02.024
[8] 廖文旭. 复杂环境下无人机航迹规划算法的研究[D]. 成都: 电子科技大学, 2021. [9] 史博辉. 面向森林火情的无人机航迹规划算法研究[D]. 西安: 西安理工大学, 2021. [10] 段慧瑶. 多无人机协同任务规划的研究与实现[D]. 长春: 吉林大学, 2020. [11] 徐文辉. 基于改进蚁群算法的无人机航迹规划研究[D]. 德阳: 中国民用航空飞行学院, 2020. [12] 刘紫玉, 赵丽霞, 薛建越, 等. 面向车辆路径问题的改进蚁群算法研究[J]. 河北科技大学学报, 2022, 43(1): 80-89. DOI: 10.7535/hbkd.2022yx01009 [13] 马培博, 钟麟. 基于蚁群算法的无人机侦察任务分配[J]. 无线电通信技术, 2022, 48(2): 371-375. DOI: 10.3969/j.issn.1003-3114.2022.02.024 [14] 毕天枢. 多无人机协同任务分配和航迹规划算法研究[D]. 北京: 北京邮电大学, 2020. [15] 韩晓微, 韩震, 岳高峰, 等. 救灾无人机的优化A*航迹规划算法[J]. 计算机工程与应用, 2021, 57(6): 232-238. DOI: 10.3778/j.issn.1002-8331.1912-0304 -
期刊类型引用(1)
1. 宋志强,陈少博. 考虑最短转弯半径的无人机区域覆盖航迹规划. 实验室研究与探索. 2023(07): 124-129 .  百度学术
百度学术
其他类型引用(1)



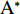

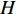


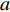
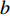
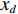
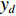
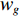
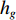
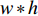
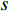
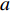
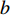
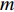
 下载:
下载: