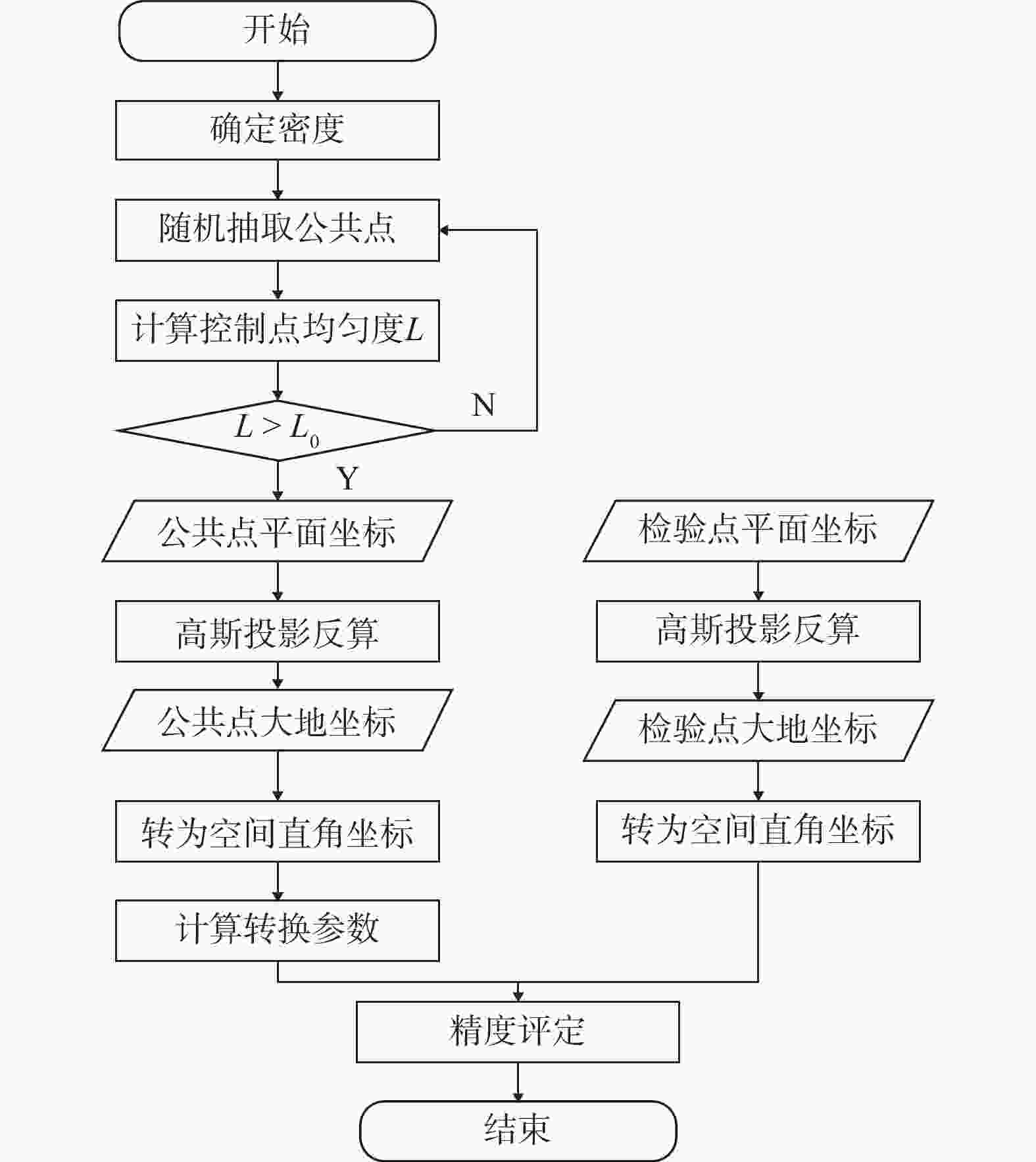
Research on coordinate transformation model considering the spatial distribution of control points
-
摘要: 针对目前坐标转换中公共点选取缺乏依据、坐标转换精度难以保证的问题，研究了基于控制点空间分布的坐标转换模型. 提出了控制点均匀度的概念，研究了控制点均匀度和密度的表达方法，分析了公共点均匀度和密度对坐标转换模型精度的影响，构建了顾及控制点空间分布的坐标转换模型，探讨了地方坐标系与CGCS2000的坐标转换流程，并结合实例验证了该模型的有效性.Abstract: To guarantee the accuracy of coordinate transformation, a coordinate transformation model was studied through selecting the proper coincident points based on the spatial distribution of control points. With the models to describe the uniformity and density of control points set up, the influence of uniformity and density of coincident points on the accuracy of coordinate transformation model was discussed. A coordinate transformation model was constructed with the spatial distribution of control points taken into account, and the coordinate transformation process between the local coordinate system and CGCS2000 was discussed. At last, the effectiveness of the new model was verified with examples.
-
Key words:
- coordinate transformation /
- monopolized circle /
- coincident point /
- uniformity /
- density
-
表 1 控制点密度与转换精度关系
控制点$t$ $ {d_{{\text{min}}}} $/m ${\overline \sigma _{{\text{in}}}}$/mm ${\overline \sigma _{{\text{out}}}}$/mm ${\overline \sigma _{{\text{out}}}}$占比/% 0～1.5 mm 1.5～3 mm >3 mm 3 46 429 0.685 3.418 9.5 61.9 28.6 5 35 964 0.726 1.921 21.1 73.6 5.3 7 30 395 0.828 1.852 11.1 88.9 0 9 26 806 0.807 1.778 18.3 81.7 0 11 24 246 0.872 1.705 7.4 92.6 0 13 22 303 0.912 1.709 3.7 96.3 0 15 20 763 0.924 1.716 0 100.0 0 
下载: 导出CSV
-
[1] 王阿昊, 王解先, 陈俊平. 同时考虑公共点新老坐标误差的三维坐标转换模型[J]. 全球定位系统, 2016, 41(5): 61-65. [2] 陈宇, 白征东, 罗腾. 基于改进的布尔莎模型的坐标转换方法[J]. 大地测量与地球动力学, 2010, 30(3): 71-73,78. [3] 方兴, 曾文宪, 刘经南, 等. 三维坐标转换的通用整体最小二乘算法[J]. 测绘学报, 2014(11): 1139-1143. [4] 刘忠贺, 李宗春, 郭迎钢, 等. 利用RANSAC算法筛选坐标转换中相对稳定公共点[J]. 测绘科学技术学报, 2019, 36(5): 487-493. [5] 王玉成, 胡伍生. 坐标转换中公共点选取对于转换精度的影响[J]. 现代测绘, 2008, 31(5): 13-15. DOI: 10.3969/j.issn.1672-4097.2008.05.004 [6] 焦立芬. 基于坐标转换重合点的分布、密度、精度与转换精度分析[J]. 测绘技术装备, 2013(4): 25-28. DOI: 10.3969/j.issn.1674-4950.2013.04.008 [7] 周跃寅, 潘国荣. 公共点分布对坐标转换精度的影响[J]. 大地测量与地球动力学, 2013(2): 105-109. [8] 罗传文. 点空间分析-分维与均匀度[J]. 科技导报, 2004(10): 51-54. DOI: 10.3321/j.issn:1000-7857.2004.10.014 [9] 陆权. 点集空间分布特征的分形描述方法[D]. 成都: 西南交通大学, 2019. [10] 王解先, 邱杨媛. 高程误差对七参数转换的影响[J]. 大地测量与地球动力学, 2007, 27(3): 25-27,38. -
点击查看大图
图(3) / 表(1)
计量
- 文章访问数: 408
- HTML全文浏览量: 131
- PDF下载量: 19
- 被引次数: 0
