Research on GPS elevation fitting method for linear engineering
-
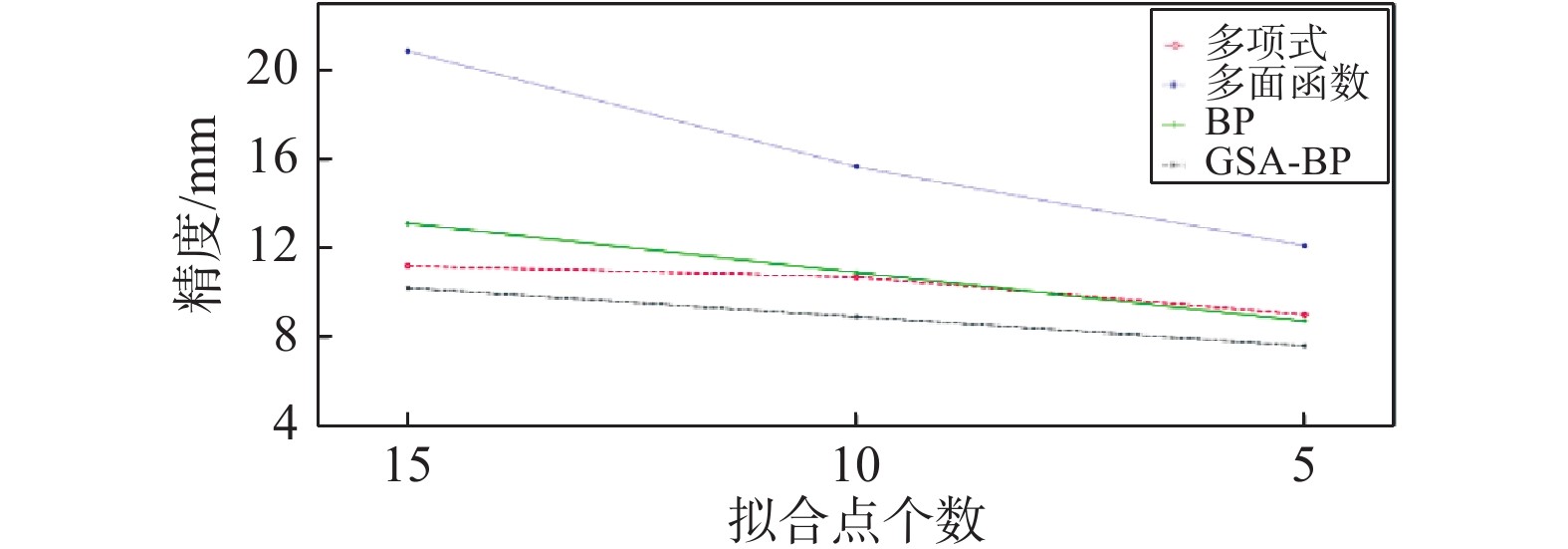
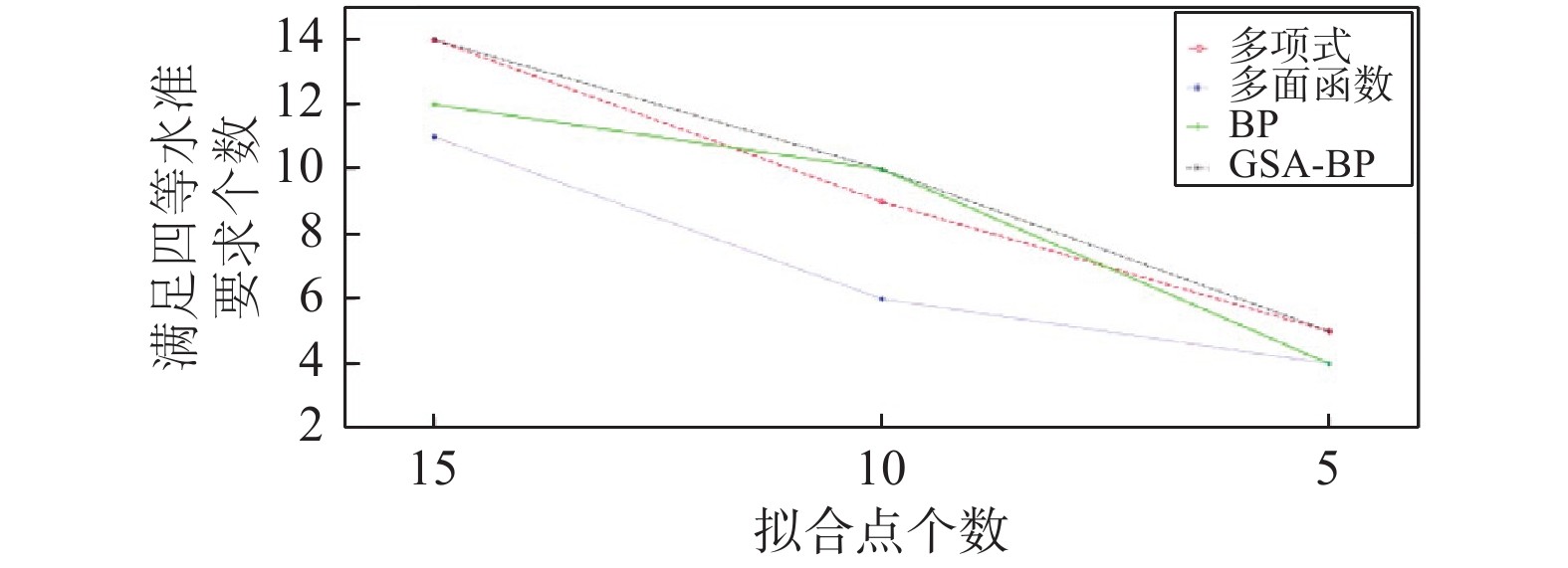
摘要: 针对数学模型只适用于特定地形和神经网络模型易陷入局部最优解的特点，提出了最优加权算法，分别利用两种数学模型和两种神经网络模型进行线状工程GPS高程拟合，并将每种模型拟合效果好的单一算法组合成最优加权算法. 结果显示：多项式拟合法优于多面函数法，遗传模拟退火算法优化BP神经网络算法(GSA-BP)优于其他算法，为最优单一算法；加权算法比其单一成员算法精度分别提高17.7%、10.0%，且能基本满足四等水准测量要求，在线状工程GPS高程拟合中具有可行性.Abstract: Aiming at the characteristics that mathematical models are only applicable to specific terrain and neural network models are easy to fall into local optimal solution, an optimal weighting algorithm is proposed. Two mathematical models and two neural network models are used to fit the GPS elevation of linear engineering respectively, and a single algorithm with good fitting effect of each model is combined into an optimal weighting algorithm. The results show that the polynomial fitting algorithm is superior to the multifaceted function method, and the genetic simulated annealing algorithm optimized BP neural network algorithm (GSA-BP) is better than other algorithms, which is the best single algorithm. The precision of the weighted algorithm is 17.7% and 10.0% higher than that of the single member algorithm, respectively, and can basically meet the requirements of the fourth grade leveling, which is feasible in GPS elevation fitting of linear engineering.
-
Key words:
- elevation anomaly /
- polynomial fitting /
- BP neural network /
- weighted /
- fourth level
-
表 1 不同方案下拟合结果对比表
方案 精度/mm 满足四等水准要求点数 多项式 多面
函数BP GSA-BP 多项式 多面
函数BP GSA-BP A 11.2 20.9 13.1 10.2 14 11 12 14 B 10.7 15.7 10.9 8.9 9 6 10 10 C 9.0 12.1 8.7 7.6 5 4 4 5 
下载: 导出CSV
表 2 拟合结果对比表
点号 最近点
距离/km四等水准
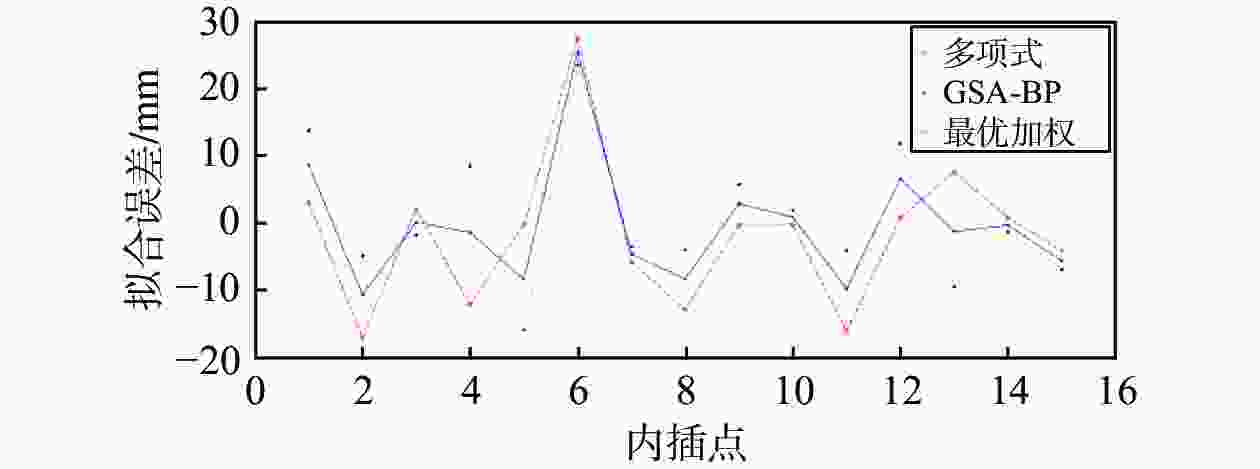
限差/mm拟合误差/mm 多项式 GSA-BP 最优加权 D04 2.1 42.7 3.1 13.8 8.7 D10 0.9 17.9 −17.1 −4.9 −10.7 D20 1.0 19.2 2.1 −1.8 0.1 D26 1.3 26.6 −12.2 8.5 −1.4 D30 1.2 23.7 −0.2 −15.9 −8.4 D02 1.2 23.6 27.6 23.6 25.5 D14 1.1 22.8 −5.8 −3.5 −4.6 D16 1.0 20.4 −12.9 −4.0 −8.3 D18 0.8 15.4 −0.2 5.8 2.9 D24 0.8 16.6 −0.2 1.9 0.9 D06 1.1 21.5 −16.1 −4.1 −9.8 D08 1.1 22.9 0.8 11.9 6.6 D12 0.5 9.6 7.6 −9.5 −1.3 D22 1.1 21.8 0.8 −1.3 −0.3 D28 0.6 11.1 −4.1 −6.9 −5.6
下载: 导出CSV
表 3 拟合精度统计表
精度/mm 加权精度提高/% 满足四等水准要求点数 多项式 GSA-BP 最优
加权多项式 GSA-BP 多项式 GSA-BP 最优
加权11.2 10.2 9.2 17.7 10.0 14 14 14
下载: 导出CSV
-
[1] 魏二虎, 刘学习, 刘经南. 北斗+GPS组合单点定位精度评价与分析[J]. 测绘通报, 2017(5): 1-5. [2] 吕建伟, 张志华, 张新秀, 等. 二次曲面与最小二乘配置的组合模型在GPS高程异常拟合中的应用[J]. 测绘通报, 2020(5): 127-129,133. [3] 唐丽娟. GPS高程转换方法研究及精度分析[J]. 全球定位系统, 2017, 42(6): 88-91. [4] 陈智伟, 张兴福, 胡波, 等. 利用RBF实现线状工程中GNSS高程转换的精度分析[J]. 测绘通报, 2018(12): 79-82,86. [5] 董洲洋, 徐卫明, 庄昊, 等. 基于深度学习的GPS水准拟合方法[J]. 测绘科学, 2021, 46(4): 57-62. [6] 王珍, 程垒. GPS高程拟合方法的研究和应用[J]. 测绘通报, 2015(增刊1): 99-102. [7] 张怀亮, 李晓莉, 朱赛虎. 改进多面函数拟合跨带区域高程异常的研究[J]. 测绘科学, 2016, 41(3): 132-137. [8] 魏宗海. 几种改进的BP神经网络在GPS高程拟合中的应用比较[J]. 全球定位系统, 2016, 41(5): 99-103. [9] 张兴福, 于红波. 模型拟合法进行GPS高程转换的研究及软件开发[J]. 广东工业大学学报, 2008, 25(3): 61-65. DOI: 10.3969/j.issn.1007-7162.2008.03.016 [10] FUNAHASHI K I. On the approximate realization of continuous mappings by neural networks[J]. Neural networks, 1989, 2(3): 183-192. DOI: 10.1016/0893-6080(89)90003-8 [11] HORNIK K. Approximation capabilities of multilayer feedforward networks[J]. Neural networks, 1991, 4(2): 251-257. DOI: 10.1016/0893-6080(91)90009-T [12] 黎剑. 区域GPS高程异常拟合及建模方法研究[D]. 昆明: 昆明理工大学, 2013. -
点击查看大图
图(6) / 表(3)
计量
- 文章访问数: 301
- HTML全文浏览量: 127
- PDF下载量: 20
- 被引次数: 0
