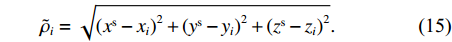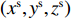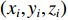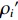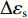Reduced-dynamic and kinematic orbit determination of Jason-3 based on satellite-borne GPS data
-
摘要: 利用Jason-3星载GPS观测数据,采用简化动力学方法和运动学方法对Jason-3卫星进行精密定轨研究. 通过载波相位残差、重叠轨道对比、参考轨道对比和卫星激光测距(SLR)轨道检核四种方式评定轨道精度. 计算相位残差均方根(RMS)值,简化动力学轨道的RMS值在0.7~0.8 cm,运动学轨道的RMS值在0.50~0.55 cm;简化动力学轨道重叠部分径向RMS值达到0.32 cm,运动学轨道重叠部分径向RMS值达到1.12 cm;与国际DORIS服务(IDS)官方提供的参考轨道对比,简化动力学轨道径向精度达到1.47 cm,运动学轨道径向精度达到4.36 cm;利用SLR观测数据进行核验,简化动力学轨道精度整体优于2.1 cm,运动学轨道精度整体优于3.3 cm. 通过实验证明:Jason-3卫星的简化动力学轨道和运动学轨道的精度均达到cm级.Abstract: The satellite-borne GPS data are used to determine precise orbit of Jason-3 satellite with the reduced-dynamic method and the kinematic method. The orbital accuracy is assessed by the carrier phase residual analysis, overlapping orbit comparison, comparison with reference orbit and satellite laser ranging (SLR) checks. The result show that the variation range of phase residuals for reduced-dynamic orbit is 0.7 cmto 0.8 cm, the variation range of phase residuals for kinematic orbit is 0.50 cm to 0.55 cm. The radial root mean square (RMS) error of the reduced-dynamic overlapping orbits is 0.32 cm, and the same error of the kinematic overlapping orbits is 1.12 cm. Compared with the reference orbits released by international DORIS service(IDS), the radial RMS of reduced-dynamic orbits is about 1.47 cm, and the radial RMS of kinematic orbits is about 4.36 cm. Results of SLR checks show that the reduced-dynamic orbital accuracy is better than 2.1 cm, and the kinematic orbital accuracy is better than 3.3 cm. The experimental results proved that the accuracy of both reduced-dynamic and kinematic orbits of Jason-3 altimetry satellite were at centimeter level, which could meet the accuracy requirements of satellite orbit.
-
Keywords:
- Jason-3 /
- satellite-borne GPS /
- precise orbit determination /
- reduced-dynamic method /
- kinematic method /
- SLR check
-
0. 引 言
Jason-3卫星是由美国国家海洋和大气管理局(NOAA)、欧洲气象卫星开发组织(EUMETSAT)、法国空间研究中心(CNES)等组织合作开发的测高卫星,于2016年1月17日发射. 作为OSTM/Jason-2卫星的继任卫星,Jason-3卫星需要继续承担TOPEX/Poseidon、Jason-1和OSTM/Jason-2卫星的任务,为全球气候预测和海洋地形研究提供高精度的监测数据. 对于测高卫星,高精度的卫星轨道可以保障卫星测高数据的高精度处理,因此对于Jason-3卫星的精密定轨至关重要,其轨道径向精度要求达到厘米级[1].
随着星载GPS接收机的发展和应用,星载GPS技术日益成熟,并且星载GPS观测数据多,数据精度高,因此星载GPS定轨技术逐渐成为低轨卫星精密轨道确定的重要手段[2]. 目前,星载GPS定轨技术已成功应用于TOPEX/Poseidon、Jason-1、OSTM/Jason-2和HY-2A等多颗测高卫星以及CHAMP、GRACE和SWARM等多颗重力卫星. 根据是否使用动力学信息,LEO卫星定轨方法可以分为运动学(Kinematic)法、动力学(Dynamic)法和简化动力学(Reduced-dynamic)法.
动力学法定轨的原理是通过精确解算带有各种力学模型的动力学方程,根据最小二乘法得到顾及各个历元观测值的轨道参数,积分得到卫星位置. 该方法能以较少的GPS观测数据得到可靠的卫星轨道,但是涉及到的力学模型较多,动力学方程复杂. 目前关于动力学定轨的研究较少,郭金运[3]等利用星载GPS双差数据对CHAMP卫星进行动力学定轨,定轨精度达到亚分米级;张德成等[4]利用星载GPS数据,采用非差动力学法定轨,获得GRACE卫星的精密轨道,定轨精度达到cm级.
简化动力学法定轨的过程与动力学定轨相似,但与动力学定轨的差异在于其使用的力学模型比动力学定轨少. Yunck T等[5]最早提出了简化动力学方法,基于星载GPS观测数据对TOPEX/Poseidon卫星进行简化动力学定轨,定轨的精度优于3 cm;随后Jäggi等[6]研究了将伪随机脉冲参数运用到定轨中,成功解算CHAMP卫星的简化动力学轨道;Haines等[7]考虑到相位中心变化(PCV),解算得到的Jason-1卫星轨道径向精度达到1 cm;秦建[8]等利用星载GPS数据,基于简化动力学方法得到GRACE卫星轨道,轨道精度达到cm级;秦建[9]等利用BERNESE5.0软件基于星载GPS观测数据对Jason-2卫星进行非差数据简化动力学定轨,轨道径向精度优于6 cm;张德志等[10]利用BERNESE5.2软件对Jason-3卫星进行简化动力学定轨,轨道径向精度优于2.2 cm;杨洲铭[11]等使用星载GPS观测数据,对GRACE-FO卫星进行简化动力学定轨研究,轨道径向精度优于2 cm;Yang[12]等提出一种监测和修复星载GPS接收机周跳的方法EEM,成功将该方法应用到SWARM-A卫星简化动力学定轨中;Qi等[13]通过添加高阶电离层延迟的改进顺序,可以提高GRACE-FO的简化动力学轨道精度.
运动学法定轨的本质是卫星空间后方交会,根据GPS卫星精密星历得到GPS卫星的位置,再结合低轨卫星的星载GPS观测数据,解算出每个历元下低轨卫星的位置. 运动学方法不受力学模型的影响,解算简单,但是数据缺失或数据观测质量下降会影响定轨的结果. 郑作亚[14]提出基于历元间加权的伪距和相位观测值联合定轨的方法,实现CHAMP卫星的运动学定轨,内符合精度达到10 cm;张守建等[15]解算得到的GRACE卫星运动学轨道精度优于4 cm;张兵兵等[16]利用星载GPS观测数据实现了SWARM系列卫星的运动学定轨,轨道径向精度达到1~2 cm.
对比研究运动学定轨和简化动力学定轨,可以更加直观的反映两种定轨方法的特点. Guo[17]等利用BERNESE5.0软件进行HY-2星载GPS数据模拟并对HY-2卫星进行定轨,定轨精度达到cm级;夏要伟等[18]使用星载GPS观测数据,基于运动学和简化动力学定轨方法,计算SWARM卫星轨道,定轨精度达到cm级.
本文基于Jason-3卫星星载GPS双频观测数据,实现Jason-3卫星的简化动力学法和运动学法精密定轨. 主要使用运动学和简化动力学方法解算精密轨道,通过设置伪随机脉冲参数吸收大气阻力和太阳光压,成功解算出Jason-3卫星的简化动力学轨道.同时,不考虑力学模型,成功解算出运动学轨道. 为了评价定轨结构,通过载波相位残差分析、重叠轨道对比、与参考轨道对比、卫星激光测距(SLR)轨道检核四种方法评价轨道精度.
1. 定轨方法及策略
1.1 观测方程
对于低轨卫星,星载GPS的双频无电离层载波相位观测方程[19]为
$$\begin{split} {l_\phi } =& \rho + c({\rm{\delta }}{t_{\rm{r}}} - {\rm{\delta }}{t^{\rm{s}}}) + \lambda \cdot N + {\rm{\delta }}{\rho _{{\rm{rel}}}} + {\rm{\delta }}{\rho _{{\rm{mul}}}}+ \\& {\rm{\delta }}{\rho _{{\rm{pco}}}} + {\rm{\delta }}{\rho _{{\rm{pcv}}}} + {\varepsilon _\phi }.\end{split}$$ (1) 式中:
${l_\phi }$ 为双频载波相位无电离层组合观测值(等效距离);$\rho $ 为低轨卫星$({x_{\rm{r}}},{y_{\rm{r}}},{z_{\rm{r}}})$ 与GPS卫星$({X^{\rm{s}}},{Y^{\rm{s}}},{Z^{\rm{s}}})$ 之间的几何距离;${\rm{\delta }}{t_{\rm{r}}}$ 为接收机钟差;${\rm{\delta }}{t^{\rm{s}}}$ 为卫星钟差;$c$ 为光速;${\rm{\delta }}{\rho _{{\rm{rel}}}}$ 为相对论改正;${\rm{\delta }}{\rho _{{\rm{mul}}}}$ 为多路径效应;${\rm{\delta }}{\rho _{{\rm{pco}}}}$ 和${\rm{\delta }}{\rho _{{\rm{pcv}}}}$ 分别为星载GPS接收机天线相位中心偏差与天线相位中心变化;$\lambda $ 为相应的波长;$N$ 为整周模糊度参数;${\varepsilon _\phi }$ 为载波相位观测数据残差.若测站的近似坐标为
$({x_0},{y_0},{z_0})$ 、接收机钟差的初始值为${\left( {{\rm{\delta }}{t_{\rm{r}}}} \right)_0}$ 和模糊度参数的初始值为${N_0}$ 作为初始值,对式(1)进行线性化. 其中${x_{\rm{r}}} = {x_0} + \Delta {x_{\rm{r}}}$ ;${y_{\rm{r}}} = {y_0} + $ $ \Delta {y_{\rm{r}}}$ ;${z_{\rm{r}}} = {z_0} + \Delta {z_{\rm{r}}}$ ;${\rm{\delta }}{t_{\rm{r}}} = {\left( {{\rm{\delta }}{t_{\rm{r}}}} \right)_0} + \Delta {\rm{\delta }}{t_{\rm{r}}}$ ;$B = {B_0} + \Delta B$ ,B为双频消电离层组合模糊度的等效距离[20]. 用泰勒级数展开,保留一阶项为$$\begin{split}{l_\phi } - {\rho _0} =& \frac{{{X^{\rm{s}}} - {x_0}}}{{{\rho _0}}}\Delta {x_{\rm{r}}} + \frac{{{Y^{\rm{s}}} - {y_0}}}{{{\rho _0}}}\Delta {y_{\rm{r}}} + \frac{{{Z^{\rm{s}}} - {z_0}}}{{{\rho _0}}}\Delta {z_{\rm{r}}} +\\& c \cdot \Delta {\rm{\delta }}{t_{\rm{r}}} + \Delta B. \end{split}$$ (2) 整理得线性化后的误差方程
$${{V}} = {{A}}x - {{L}}.$$ (3) 式中:
${{V}}$ 为观测值残差向量;${{A}}$ 为系数矩阵;$x$ 为未知参数改正量;${{L}}$ 为常数向量.1.2 动力学法
低轨卫星在飞行过程中,会受到多种力的作用,包括地球引力、日月引力、地球非球形摄动、潮汐摄动、大气阻力、太阳辐射压、地球辐射压以及相对论效应等影响[21],其运动微分方程[22]为
$${\ddot{ r}} = - \frac{{GM}}{{{{{r}}^3}}}{{r}} + {{{f}}_1}({t_1},{{r}},{{\dot r}},{q_1}, \cdots ,{q_d}).$$ (4) 式中:
${{r}}$ 、${{\dot r}}$ 、${\ddot{ r}}$ 分别表示卫星的位置、速度和加速度向量;初始条件表示为${{r}}({t_0}) = {{r}}(a,e,i,\varOmega ,\omega ,{{T}_0};{t_0})$ 、${{\dot r}}({t_0}) = {{\dot r}} $ $ (a,e,i,{{\varOmega}} ,\omega ,{{T}_0};{t_0})$ ,其中,$(a,e,i,\varOmega ,\omega ,{{T}_0};{t_0})$ 为在参考历元${t_0}$ 下的6个开普勒元素;${f_1}$ 为扰动加速度;$({q_1}, \cdots , $ $ {q_d})$ 表示未知的扰动力参数;$GM$ 表示地球万有引力常量.根据测码伪距可得到先验轨道
${{{r}}_0}(t)$ ,动力学法定轨可以看作是一个逐渐改善轨道的过程. 其本质是根据最小二乘的方法得到顾及各个历元观测值的轨道参数. 假设有$n$ 个历元的观测值,初始历元的轨道参数为${{{p}}_0}$ ,利用数值积分得到$({t_i},{t_0})$ 时段的状态转移矩阵${{\varPhi }}({t_i},{t_0})$ ,${{{p}}_i} = {{\varPhi }}({t_i},{t_0}){{{p}}_0}$ ,可建立观测方程[22]$$ {\begin{bmatrix} {{{{V}}_0}} \\ \vdots \\ {{{{V}}_i}} \\ \vdots \\ {{{{V}}_n}} \end{bmatrix}} = \left[\!\!\!\! {\begin{array}{*{20}{c}} {{{{A}}_0}} \\ \vdots \\ {{{{A}}_i}{{\varPhi }}({t_i},{t_0})} \\ \vdots \\ {{{{A}}_n}{{\varPhi }}({t_n},{t_0})} \end{array}} \!\!\!\!\right]{{{p}}_0} - \left[\!\!\!\! {\begin{array}{*{20}{c}} {{L_0}} \\ \vdots \\ {{L_i}} \\ \vdots \\ {{L_n}} \end{array}} \!\!\!\!\right].$$ (5) 式(5)也可以写成
${{V}} = {{B\varPhi }}{{{P}}_0} - {{L}}$ ,其中,${{V}}$ 为观测数据残差向量矩阵,${{B}}$ 表示由观测数据构建的误差方程的系数矩阵,${{L}}$ 表示常数项矩阵.1.3 简化动力学
由于低轨卫星所在的空间环境复杂,动力学模型难以对大气阻力和太阳光压进行模式化处理,因此动力学定轨精度不可避免的受到未被模式化的摄动因素的影响.
在卫星定轨过程中,每隔一段时间,在特定的历元上对卫星径向(R)、切向(T)和法向(N)设置一组瞬时变化值,该值称为伪随机脉冲. 在简化动力学求解卫星轨道的过程中引入伪随机脉冲参数,每周期估计一次脉冲作为制约因子,以改善太阳光压误差[23].
简化动力学方法计算卫星轨道与动力学法类似,都是采用力学模型与数值积分求解卫星轨道,但差异在于简化动力学方法所使用的力学模型比动力学方法少,简化动力学方法通过附加伪随机参数,平衡了动力学与运动学两方法,通过不断迭代求解改善轨道质量,使得定轨结果更加准确.
1.4 运动学法
运动学法是指利用星载GPS观测数据和地面站的跟踪数据,根据空间距离后方交会的原理,解算卫星轨道的方法. 运动学法定轨的优点是解算过程简单,不受低轨卫星动力学模型的影响,但是解算出的轨道是离散的点位,需要拟合后得到连续轨道[24-25]. 运动学定轨精度主要受到GPS数据质量的影响,包括GPS观测数据的质量,GPS卫星数量和空间结构,GPS卫星轨道和钟差质量等[26].
在GPS数据处理过程中,参数数量非常庞大,无法使用常规的最小二乘方法. 需要通过最小二乘方法中的参数消元法分类处理不同的参数,以提高解算效率. 在动态定位中,测站位置和接收机钟差参数与时间相关,而对于整周模糊度参数,若不发生周跳,可以将整周模糊度参数当作常数. 因此,先将这些与时间相关的参数从法方程中消去,只解算与历元变化无关的参数;得到这些与历元变化无关的参数后带回到初始方程,再逐历元解算提前消掉与时间有关的参数.
对式(1)进行线性化后,历元
$i$ 的误差方程为$${{{V}}_i} = {{{A}}_i}{{{x}}_i} + {{{B}}_i}{{y}} - {{{L}}_i}{{{p}}_i}\;\;.$$ (6) 式中:
${{{V}}_i}$ 为历元$i$ 线性化观测值残差向量;${{{x}}_i}$ 表示与历元$i$ 相关的参数(测站坐标、接收机钟差)改正量;${{y}}$ 表示在此观测时间内的整周模糊度参数改正量;${{{A}}_i}$ 和${{{B}}_i}$ 分别为相应参数的系数矩阵;${{{L}}_i}$ 为历元$i$ 的线性化常数阵;${{{p}}_i}$ 为历元$i$ 的权矩阵.式(6)的法方程为
$$ {\begin{bmatrix} {{{A}}_i^{\rm{T}}{{{P}}_i}{{{A}}_i}}&{{{A}}_i^{\rm{T}}{{{P}}_i}{{{B}}_i}} \\ {{{B}}_i^{\rm{T}}{{{P}}_i}{{{A}}_i}}&{{{B}}_i^{\rm{T}}{{{P}}_i}{{{B}}_i}} \end{bmatrix}} \cdot {\begin{bmatrix} {{{{x}}_i}} \\ {{y}} \end{bmatrix}} = {\begin{bmatrix} {{{A}}_i^{\rm{T}}{{{P}}_i}{{{L}}_i}} \\ {{{B}}_i^{\rm{T}}{{{P}}_i}{{{L}}_i}} \end{bmatrix}}.$$ (7) 式中,
$i \!=\!\! 1,2, \cdots ,n$ . 令$\left[\!\!\!\! {\begin{array}{*{20}{c}} {{{{N}}_{{{xx}},i}}}&{{{{N}}_{{{xy}},i}}} \\ {{{{N}}_{{{yx}},i}}}&{{{{N}}_{{{yy}},i}}} \end{array}} \!\!\!\!\right] \!\!=\!\! \left[\!\!\!\! {\begin{array}{*{20}{c}} {{{A}}_i^{\rm{T}}{{{P}}_i}{{{{\rm A}}}_i}}&{{{A}}_i^{\rm{T}}{{{P}}_i}{{{B}}_i}} \\ {{{B}}_i^{\rm{T}}{{{P}}_i}{{{A}}_i}}&{{{B}}_i^{\rm{T}}{{{P}}_i}{{{B}}_i}} \end{array}} \!\!\!\!\right]$ ,$\left[\!\!\!\! {\begin{array}{*{20}{c}} {{{{U}}_{{{x}}.i}}} \\ {{{{U}}_{{{y}}.i}}} \end{array}}\!\!\!\! \right] = \left[\!\!\!\! {\begin{array}{*{20}{c}} {{{A}}_i^{\rm{T}}{{{P}}_i}{{{L}}_i}} \\ {{{B}}_i^{\rm{T}}{{{P}}_i}{{{L}}_i}} \end{array}} \!\!\!\!\right]$ .当
$i = 1$ 时,消去随历元变化的参数${{x}_1}$ ,则$$ {\begin{bmatrix} {{{{N}}_{{{xx}},1}}}&{{{{N}}_{{{xy}},1}}} \\ {{{{N}}_{{{yx}},1}}}&{{{{N}}_{{{yy}},1}}} \end{bmatrix}} \cdot {\begin{bmatrix} {{{{x}}_1}} \\ {{y}} \end{bmatrix}} = {\begin{bmatrix} {{{{U}}_{{{x}},1}}} \\ {{{{U}}_{{{y}},1}}} \end{bmatrix}} ,$$ (8) 即
$({{{N}}_{{{yy}},1}} - {{{N}}_{{{yx}},1}}{{N}}_{{{xx}},1}^{ - 1}{{{N}}_{{{xy}},1}})y = {{{U}}_{{{y}},1}} - {{{N}}_{{{yx}},1}}{{N}}_{{{xx}},1}^{ - 1}{{{U}}_{{{x}},1}}$ . 令${\overline {{N}} _{{{xy}},i}} = {{{N}}_{{{yy}},i}} - {{{N}}_{{{yx}},i}}{{N}}_{{{xx}},i}^{ - 1}{{{N}}_{{{xy}},i}}$ ,${\overline {{U}} _{{{y}},i}} = {{{U}}_{{{y}},i}} - {{{N}}_{{{yx}},i}}{{N}}_{{{xx}},i}^{ - 1}{{{U}}_{{{x}},i}}$ ,则式(6)可以表示为$${\overline {{N}} _{{{yy}},i}} \cdot {{y}} = {\overline {{U}} _{{{y}},i}}\;\;.$$ (9) 考虑第1个历元的向量
${{y}}$ 的先验信息,则第2个历元的法方程为$$ {\begin{bmatrix} {{{{N}}_{{{xx}},2}}}&{{{{N}}_{{{xy}},2}}} \\ {{{{N}}_{{{yx}},2}}}&{{{{N}}_{{{yy}},2}} + {{\overline {{N}} }_{{{yy}},1}}} \end{bmatrix}} \cdot {\begin{bmatrix} {{{{x}}_2}} \\ {{y}} \end{bmatrix}} = {\begin{bmatrix} {{{{U}}_{{{x}},2}}} \\ {{{{U}}_{{{y}},2}} + {{\overline {{U}} }_{{{y}},1}}} \end{bmatrix}}. $$ (10) 再从上式消去随历元变化的参数
${{{x}}_2}$ ,则$$\sum\limits_{i = 1}^2 {({{{N}}_{{{yy}},i}} \!-\! {{{N}}_{{{yx}},i}}{{N}}_{{{xx}},i}^{ - 1}{{{N}}_{{{xy}},i}}) \cdot } {{y}} \!=\! \sum\limits_{i = 1}^2 {({{{U}}_{{{y}},i}} \!-\! {{{N}}_{{{yx}},i}}{{N}}_{{{xx}},i}^{ - 1}{{{U}}_{{{x}},i}})}. $$ (11) 联合式(9)得
$$\sum\limits_{i = 1}^2 {{{\overline {{N}} }_{{{yy}},i}} \cdot } {{y}} = \sum\limits_{i = 1}^2 {{{\overline {{U}} }_{{{y}},i}}}\;\;. $$ (12) 以此类推,则在第n个历元消去随历元变化的参数
${{{x}}_n}$ ,相应的向量${{y}}$ 的法方程为$$\sum\limits_{i = 1}^n {{{\overline {{N}} }_{{{yy}},i}} \cdot } {{y}} = \sum\limits_{i = 1}^n {{{\overline {{U}} }_{{{y}},i}}}\;\;. $$ (13) 得到
${{y}} = {\left(\displaystyle\sum\limits_{i = 1}^n {{{\overline {{N}} }_{{{xy}},i}} \cdot } \right)^{ - 1}} \cdot \left(\displaystyle\sum\limits_{i = 1}^n {{{\overline {{U}} }_{{{y}},i}}} \right)$ . 将${{y}}$ 带回式(6)中,可以得到${{{x}}_i}$ $${{{x}}_i} = {{N}}_{{{xx}},i}^{ - 1} \cdot {{{U}}_{{{x}},i}}\;\;.$$ (14) 1.5 定轨策略
本文基于Jason-3卫星2019-01-25—01-31年积日DOY 25—31共7天的星载GPS观测数据,进行精密定轨研究. 主要采用简化动力学法和运动学法,利用Jason-3卫星7天星载GPS数据解算卫星的精密轨道,定轨弧段为24 h. 通过载波相位残差分析、重叠轨道对比、与参考轨道对比以及SLR轨道检核四种方法对比,分析Jason-3卫星简化动力学定轨和运动学定轨的精度. 简化动力学定轨的策略如表1所示.
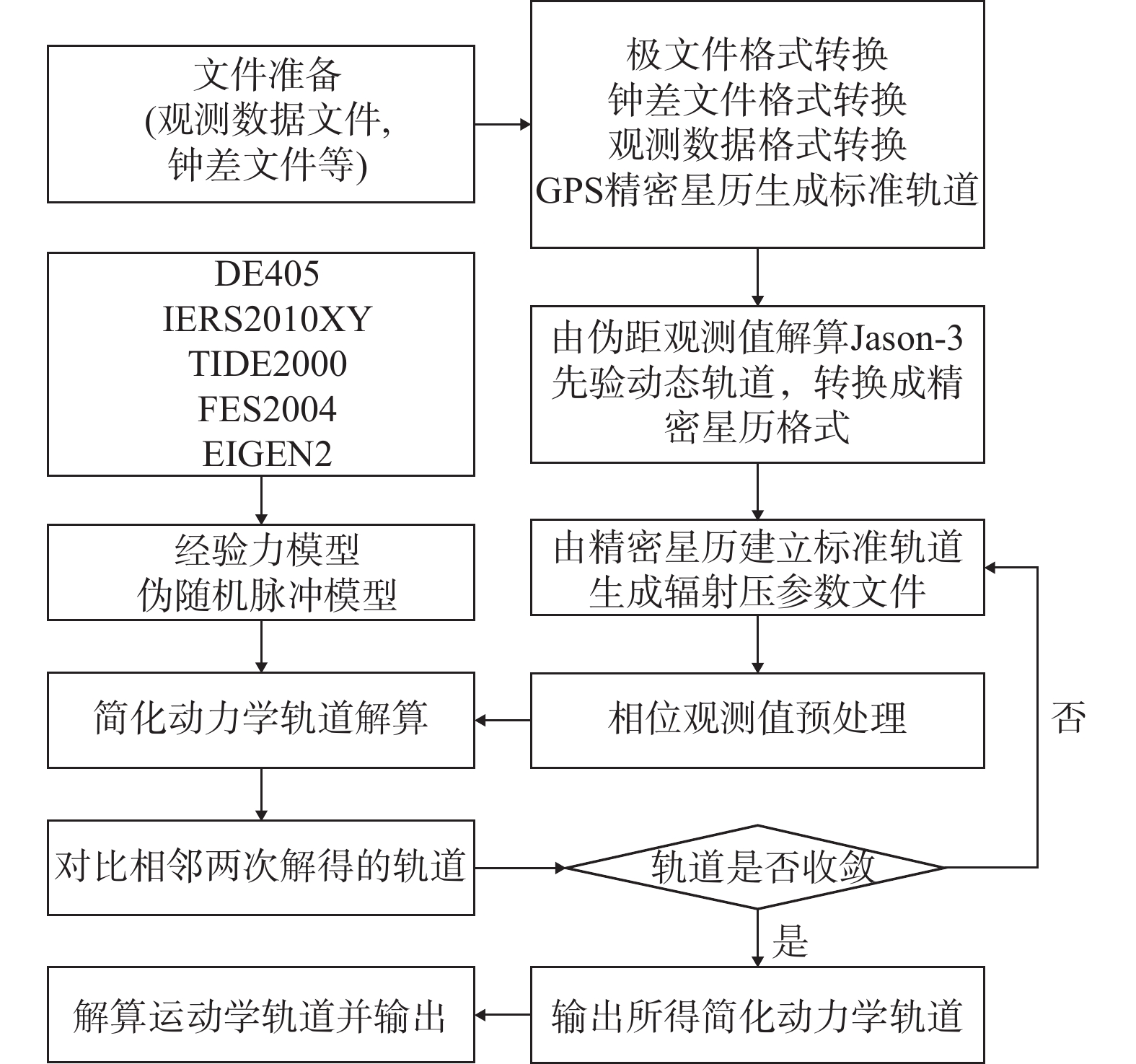
表 1 Jason-3卫星简化动力学定轨策略项目 描述 地球重力场 EIGEN2 海潮 FES2004 固体潮 TIDE2000 单日极移 IERS2010XY GPS天线相位模型 igs08.atx 伪随机脉冲参数 每15 min估计一组 截至高度角/(°) 5 采样率/s 30 参考轨道时间系统 GPST 本文利用Bernese5.2软件对Jason-3卫星定轨进行研究,简化动力学和运动学定轨的技术路线[18]如图1所示.
由于GPS观测的是从GPS卫星发射天线的相位中心到LEO卫星天线相位中心间的距离,而GPS精密星历提供的是卫星质心的坐标,因此需要进行卫星天线相位中心改正. 天线相位中心的误差通常分为两部分:天线相位中心偏差(PCO)和天线PCV;PCO指天线瞬时相位中心的平均值与天线参考点之间的距离,PCV指天线瞬时相位中心的平均值与天线瞬时相位中心的距离[27-28].
在与参考轨道对比时,需要考虑将简化动力学轨道和运动学轨道与参考轨道在时间系统上进行统一. 由于国际DORIS服务(IDS)官方网站(https://ids-doris.org)提供的Jason-3卫星参考轨道的时间系统是国际原子时(TAI),而简化动力学轨道和运动学轨道的时间系统是GPS时(GPST),TAI与GPST存在19 s的偏差,即TAI−GPST=19 s,所以需要事先对IDS提供的参考轨道做预处理,将参考轨道的时间系统转换为GPST,以方便与参考轨道对比.
2. 数据来源
本文定轨采用CNES(ftp://ftp-access.aviso.altimetry.fr)提供星载GPS双频观测数据,采样间隔为10 s,观测弧段为2019-01-25—01-31年积日DOY 25—31共7天的观察数据;采用欧洲定轨中心(CODE)(ftp://ftp.aiub.unibe.ch/CODE)提供的GPS卫星精密星历采样间隔为30 s 的卫星钟差产品、地球自转参数数据;采用IDS官方网站(https://ids-doris.org)提供的Jason-3卫星精密轨道作为参考轨道,它是法国CNES利用DORIS和GPS观测数据联合定轨解算得到的,轨道的径向精度优于1.5 cm[1,27];采用NASA官方网站(https://cddis.nasa.gov/archive/slr)提供的SLR轨道检核观测数据,其定轨精度可以达到1~2 cm. 相关数据的详细信息如表2所示.
表 2 数据来源数据文件 数据来源 星载GPS观测数据文件
(30 s)CNES(ftp://ftp-access.aviso.altimetry.fr) GPS卫星精密星历文件
(15 min)CODE(ftp://ftp.aiub.unibe.ch/CODE) GPS卫星钟差文件
(30 s)CODE(ftp://ftp.aiub.unibe.ch/CODE) 地球自转参数文件 CODE(ftp://ftp.aiub.unibe.ch/CODE) Jason-3卫星精密轨道文件(1 min) IDS(https://ids-doris.org) SLR观测数据文件 NASA(https://cddis.nasa.gov/archive/slr) 3. Jason-3卫星定轨结果与对比分析
本文对于Jason-3卫星简化动力学轨道和运动学轨道的精度检核分为内符合精度检核和外符合精度检核两个部分. 内符合精度检核采用载波相位残差分析和重叠轨道对比两种方法,外符合精度检核采用与参考轨道对比和SLR轨道检核两种方式.
3.1 载波相位残差分析
评价轨道的精度,首先要看观测数据的拟合程度. 对于简化动力学定轨而言,载波相位残差主要指模型化的误差和未被模型化的误差,因此残差均方根(RMS)值可以作为内符合精度评定的指标之一[29]. 残差RMS值越小,说明内符合精度越高
本文采用双频数据消电离层(LC)组合对星载GPS观测数据进行处理,消除电离层延迟一阶主项的影响[30]. 图2为2019-01-25—01-31年积日DOY 25—31共7天中每天的简化动力学定轨和运动学定轨两种方法定轨总的相位残差RMS值. 结果如表3所示.
表 3 载波相位残差RMS值汇总统计mm 轨道 最小值 最大值 平均值 标准差 RMS 简化动力学 4.8 22.3 7.2 2.6 7.6 运动学 3.5 15.7 5.1 1.9 5.4 对于简化动力学方法定轨,结合图2所示的每天的残差RMS值和表3统计的总残差RMS值,可以发现7天内的残差RMS值相当接近,均在7~8 mm,这说明Jason-3卫星搭载的GPS接收机获取的数据稳定,简化动力学定轨的策略得当,结果可靠.
类似地,对于运动学方法定轨,结合图2所示的每天的残差RMS值和表3统计的总残差RMS值,可以发现7天内的残差RMS值相当接近,均在5.0~5.5 mm,这说明运动学定轨没有受到力学模型等模型误差的影响,运动学定轨结果可靠.
3.2 重叠轨道对比
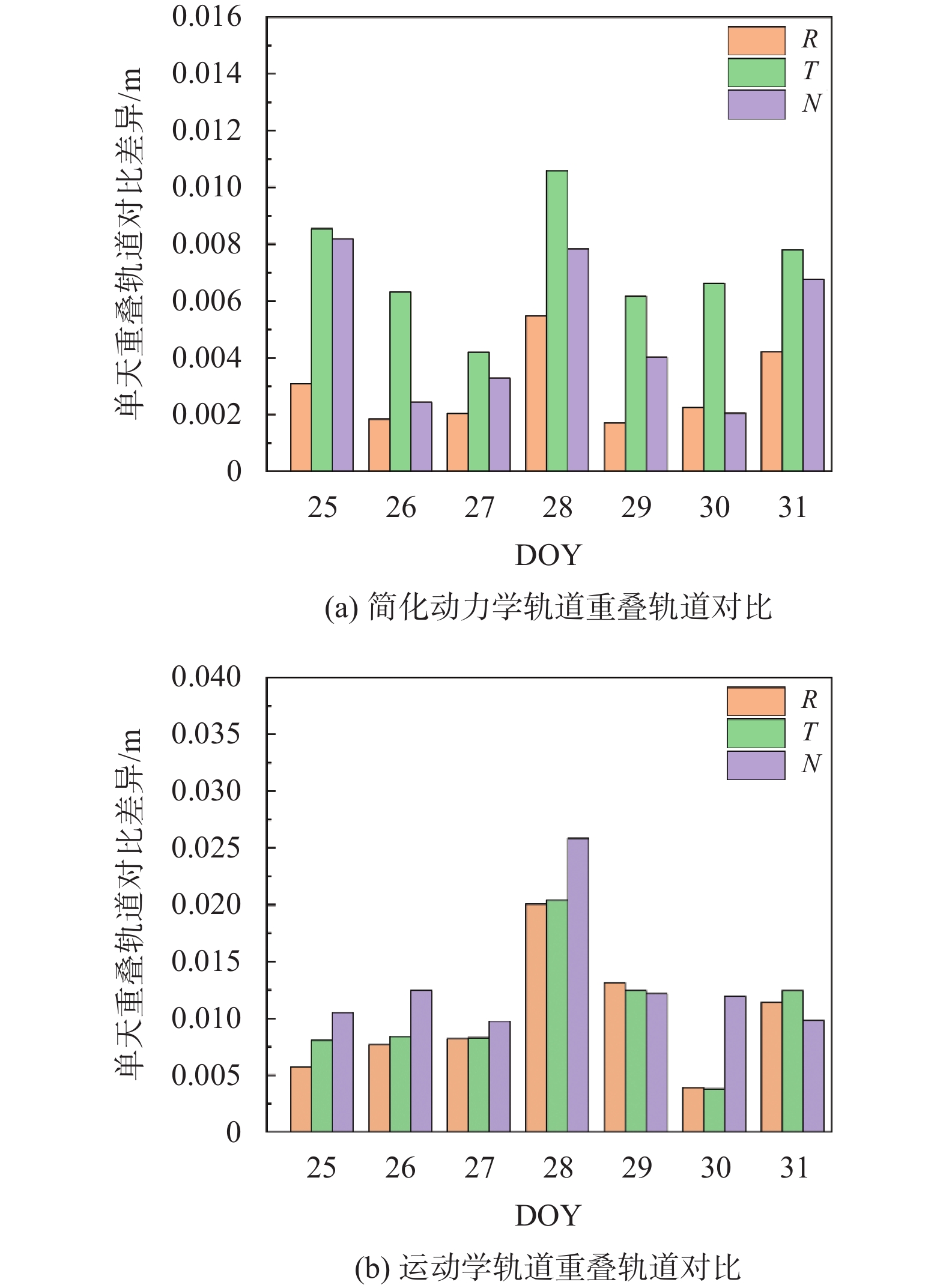
本文使用2019-01-25—01-31年积日 DOY 25—31共7天的Jason-3卫星星载GPS观测数据进行简化动力学定轨和运动学定轨,对轨道结果按照重叠时段进行对比以验证其精度. 将单天的定轨分为2个弧段进行,第一个弧段为0~18 h,第二个弧段为12~24 h,两个弧段的重叠时间为6 h. 重叠时段的轨道通过两次相互独立的定轨得到,可以通过对比重叠时段的两段轨道,来检核定轨结果的内符合精度,结果如图3所示. 汇总统计结果如表4所示.
由图3所示的单天重叠轨道对比差异图可以看出,对于简化动力学轨道,差异在R向上的RMS值在0.001~0.005 m波动;在T向上的RMS值在0.004~0.01 m波动;在N向上的RMS值在0.002~0.008 m波动. 表4所示的简化动力学轨道重叠时段对比7天汇总的结果是,重叠轨道的差异在R向上的RMS值为0.32 cm;在T向上的RMS值为0.97 cm;在N向上的RMS值为0.55 cm.
表 4 重叠轨道对比残差7天汇总统计结果cm 轨道 轨道方向 最小值 最大值 平均值 标准差 RMS 简化动力学
轨道R −1.20 1.13 −0.02 0.32 0.32 T −4.07 1.79 0.05 0.97 0.97 N −1.33 1.27 0.14 0.53 0.55 运动学轨道 R −4.55 4.70 −0.02 1.12 1.12 T −4.92 4.42 −0.10 1.16 1.16 N −1.01 4.85 1.15 0.84 1.42 类似的,对于运动学轨道,由图3可以看出,差异在R向上的RMS值在0.003~0.013 m波动;在T向上的RMS值在0.003~0.012 m波动;在N向上的RMS值在0.009~0.025 m波动. 表4所示的运动学轨道重叠时段对比7天汇总的结果是,重叠轨道的差异在R向上的RMS值为1.12 cm;在T向上的RMS值为1.16 cm;在N向上的RMS值为1.42 cm.
对Jason-3卫星进行的简化动力学轨道和运动学轨道进行重叠轨道对比,简化动力学轨道的重叠轨道对比整体差异的RMS值在R、T、N三个方向分别为0.32 cm、0.97 cm、0.55 cm,运动学轨道的重叠轨道对比整体差异的RMS值在R、T、N三个方向分别为1.12 cm、1.16 cm、1.42 cm. 统计结果表明,重叠时段轨道的差异较小,定轨内符合精度达到cm级.
3.3 与参考轨道对比
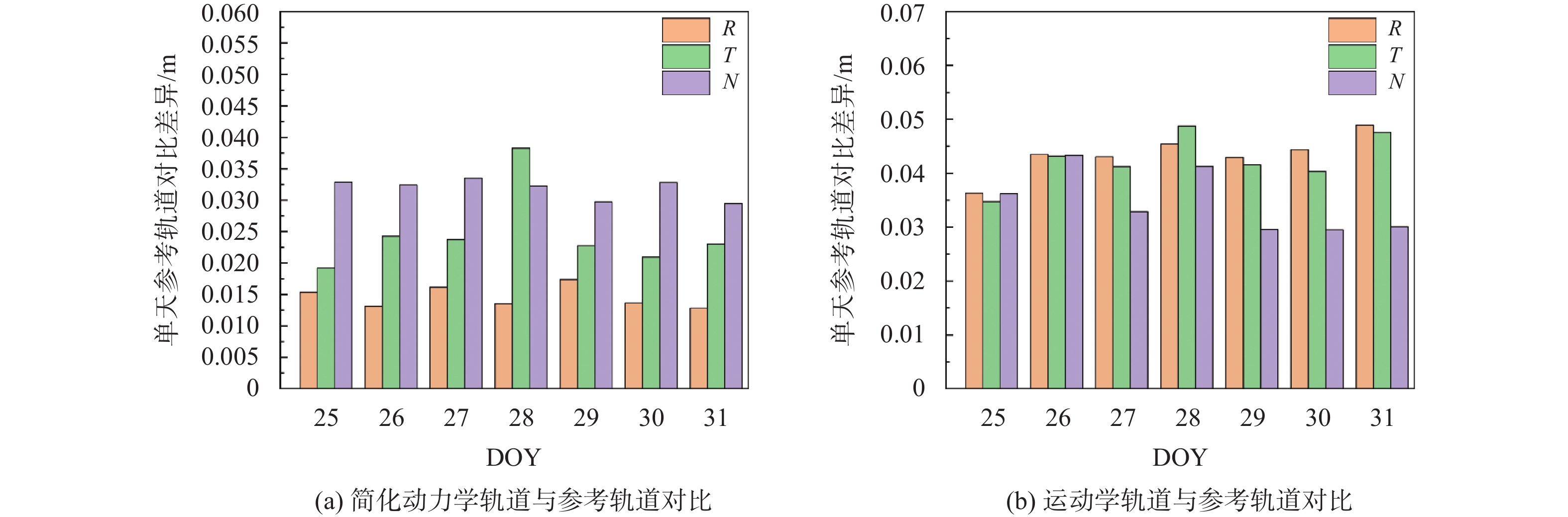
本文采用IDS官方网站(https://ids-doris.org)提供的Jason-3卫星精密轨道作为参考轨道,该轨道是CNES利用DORIS和GPS观测数据联合定轨解算得到的,轨道的径向精度优于1.5 cm[1]. 以IDS官方网站提供的精密轨道作为参考轨道,将简化动力学轨道和运动学轨道分别与之对比,得到轨道残差的RMS值对Jason-3卫星的简化动力学轨道和运动学轨道进行外符合精度评定与参考轨道对比的单天结果如图4所示. 将Jason-3卫星7天的简化动力学轨道和运动学轨道分别与参考轨道对比,统计得到的轨道残差,整体信息如表5所示.
表 5 简化动力学轨道和运动学轨道分别与参考轨道对比7天汇总结果统计cm 轨道 轨道方向 最小值 最大值 平均值 标准差 RMS 简化动力学
轨道R −12.81 7.07 −0.20 1.45 1.47 T −10.10 6.61 0.05 2.53 2.53 N −8.39 0.46 −2.95 1.21 3.19 运动学轨道 R −14.97 20.56 −0.30 4.35 4.36 T −16.41 20.43 −0.21 4.26 4.27 N −12.19 8.30 −2.18 2.75 3.51 从图4(a)可以看出,简化动力学轨道与参考轨道对比,在R向上的RMS值在0.012~0.016 m波动;在T向上的RMS值在0.019~0.038 m波动;在N向上的RMS值在0.029~0.033 m波动. 图4(a)中可以看出DOY 28的轨道残差切向精度最差;而其他6天的简化动力学轨道与参考轨道对比结果均是法向精度较差,Jason-3卫星的简化动力学轨道径向精度较高.
从图4(b)中可以看出,运动学轨道与参考轨道对比得到的轨道残差,在R向上的RMS值在0.036~0.046 m波动;在T向上的RMS值在0.034~0.047 m波动;在N向上的RMS值在0.029~0.043 m波动. 图4(b)中可以看出DOY 28的轨道残差切向精度最差;而其他6天的结果均是径向精度较差. Jason-3卫星的运动学轨道,法向精度较高.
从表5可以看出,简化动力学轨道与参考轨道对比的残差在R向上的RMS值为1.47 cm;在T向上的RMS值为2.53 cm;在N向上的RMS值为3.19 cm;整体上看,简化动力学轨道的径向精度较高. 对于运动学轨道,残差在R向上差异的RMS值为4.36 cm;在T向上差异的RMS值为4.27 cm;在N向上差异的RMS值为3.51 cm;整体上看,运动学轨道的法向精度较高. 分别将Jason-3卫星的简化动力学轨道和运动学轨道与参考轨道对比,说明定轨内符合精度达到cm级.
3.4 SLR轨道检核
卫星激光测距技术是卫星精密定轨的一种重要手段,本文选择由NASA官方网站(https://cddis.nasa.gov/archive/slr)提供的SLR观测数据,其定轨精度可以达到1~2 cm[31].
SLR轨道检核是利用轨道提供的卫星坐标和SLR台站坐标计算出站星距离,并与对应历元下SLR台站的观测数据对比,从而评定简化动力学方法和运动学法定轨的精度.
计算Jason-3卫星与SLR台站之间的距离公式为
$${\tilde \rho _i} = \sqrt {{{({x^{\rm{s}}} - {x_i})}^2} + {{({y^{\rm{s}}} - {y_i})}^2} + {{({z^{\rm{s}}} - {z_i})}^2}}. $$ (15) 式中:
$({x^{\rm{s}}},{y^{\rm{s}}},{z^{\rm{s}}})$ 为卫星的坐标;$({x_i},{y_i},{z_i})$ 为SLR台站i的坐标.将站星距归算到SLR台站到卫星质心的距离[32]
$${\rho _i}' = {\tilde \rho _i} + \Delta {\varepsilon _{\rm{s}}}.$$ (16) 式中:
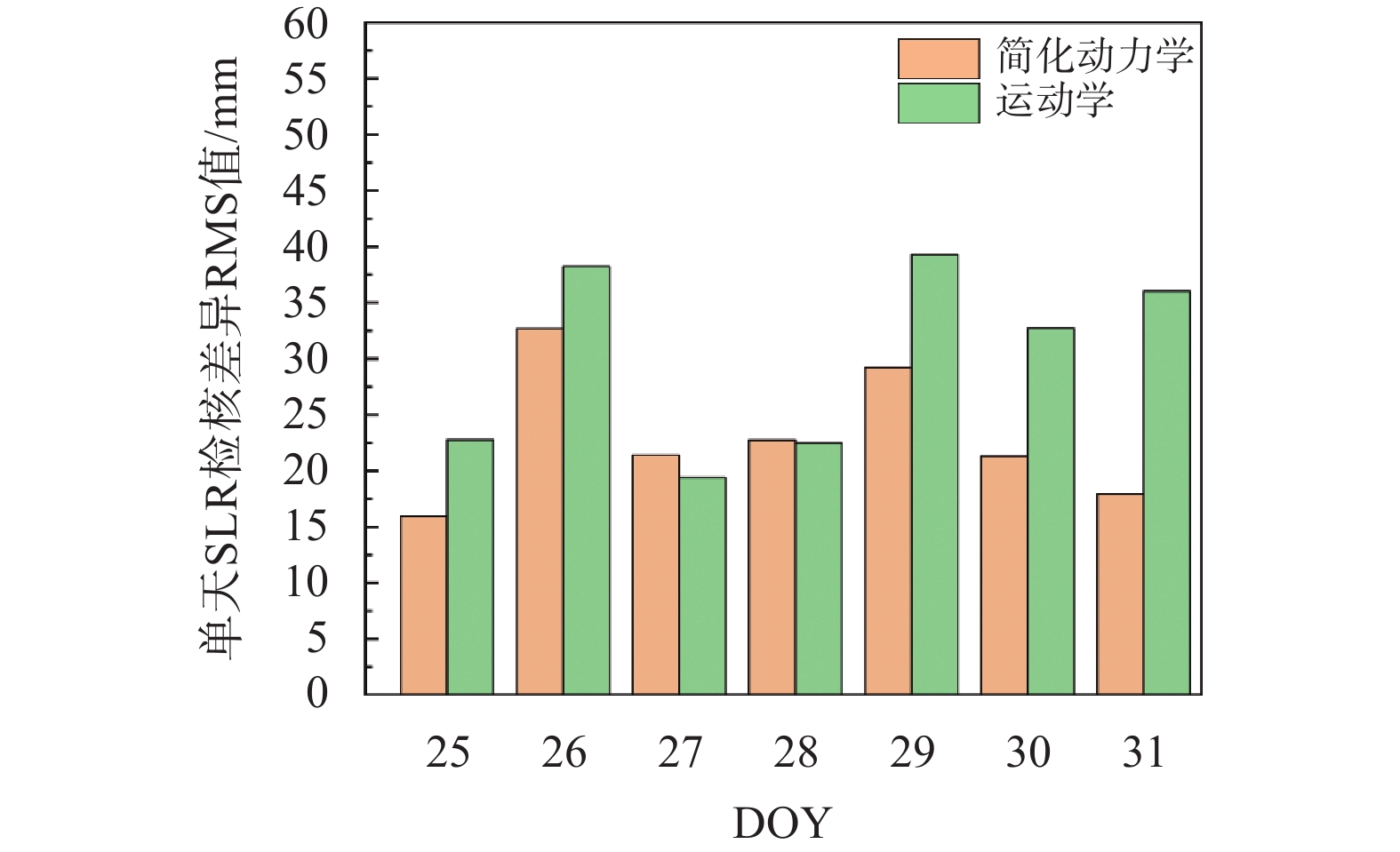
${\rho _i}'$ 为质心修正后的距离;$\Delta {\varepsilon _{\rm{s}}}$ 为卫星天线相位中心到卫星质心的修正.由于SLR轨道检核数据包含一些误差,如对流层折射等,因此需要对SLR轨道检核观测数据进行预处理,观测数据的预处理主要包括对流层折射、广义相对论、质心补偿、测站偏心修正等[33]. 比较SLR台站的观测值与由轨道提供的卫星坐标和SLR台站坐标计算的距离值,统计SLR轨道检核残差的RMS值,将单天的RMS值绘制成如图5所示的柱状图.
如图5所示,可知简化动力学轨道的SLR轨道检核残差RMS值在15~32 mm,而运动学轨道的SLR轨道检核残差RMS值在19~39 mm.
如表6所示,Jason-3卫星共有7个测站901个NP(Normal Point)数据,分别汇总统计SLR轨道检核的残差,简化动力学轨道的SLR轨道检核残差RMS值为2.41 cm,运动学轨道的SLR轨道检核残差RMS值为3.28 cm. 实验结果说明简化动力学轨道精度整体优于2.1 cm,运动学轨道精度整体优于3.3 cm. 这说明Jason-3卫星轨道的外符合精度可达cm级,定轨精度较高.
表 6 SLR轨道检核7天汇总结果统计cm 轨道 测站数 NP数 最小值 最大值 平均值 标准差 RMS 简化
动力学
轨道7 901 −3.18 3.23 0.82 0.69 2.02 运动学轨道 7 901 −0.84 8.29 −0.40 1.26 3.28 4. 结 语
本文利用Jason-3卫星星载GPS观测数据,基于简化动力学方法和运动学方法解算Jason-3卫星的轨道,并通过载波相位残差分析、重叠轨道对比、参考轨道对比和SLR轨道检核进行精度评定,得到如下结论:
1)通过相位残差RMS值可以看出,简化动力学轨道的相位残差RMS在0.7~0.8 cm,运动学轨道的相位残差RMS在0.50~0.55 cm. 这说明Jason-3卫星定轨策略可靠,在解算轨道过程中误差项消除较为理想,定轨结果较为稳定.
2)分别将Jason-3卫星两个时段的简化动力学轨道和运动学轨道重叠对比,得到7天的重叠轨道对比汇总的结果. 简化动力学轨道重叠时段R向上差异的RMS值为0.32 cm,T向上差异的RMS值为0.97 cm,N向上差异的RMS值为0.55 cm;运动学轨道重叠时段R向上差异的RMS值为1.12 cm,T向上差异的RMS值为1.16 cm,N向上差异的RMS值为1.42 cm. 这说明简化动力学定轨和运动学定轨的内符合精度均达到cm级.
3)分别将Jason-3卫星的简化动力学轨道和运动学轨道与IDS官网提供的精密轨道对比,得到7天汇总的结果. 简化动力学轨道与参考轨道对比得到的残差在R向上的RMS值为1.47 cm,在T向上的RMS值为2.53 cm,在N向上的RMS值为3.19 cm;运动学轨道与参考轨道对比得到的残差在R向上的RMS值为4.36 cm,在T向上的RMS值为4.27 cm,在N向上的RMS值为3.51 cm. 这说明简化动力学轨道和运动学轨道的外符合精度均达到cm级.
4)利用NASA提供的SLR轨道检核观测数据对Jason-3卫星的简化动力学轨道和运动学轨道精度进行检验,证明简化动力学轨道精度整体优于2.1 cm,运动学轨道精度整体优于3.3 cm. 这说明Jason-3卫星的轨道外符合精度达到cm级.
从本文实验结果来看,Jason-3卫星的简化动力学轨道和运动学轨道均达到cm级的精度.
-
表 1 Jason-3卫星简化动力学定轨策略
项目 描述 地球重力场 EIGEN2 海潮 FES2004 固体潮 TIDE2000 单日极移 IERS2010XY GPS天线相位模型 igs08.atx 伪随机脉冲参数 每15 min估计一组 截至高度角/(°) 5 采样率/s 30 参考轨道时间系统 GPST 表 2 数据来源
数据文件 数据来源 星载GPS观测数据文件
(30 s)CNES(ftp://ftp-access.aviso.altimetry.fr) GPS卫星精密星历文件
(15 min)CODE(ftp://ftp.aiub.unibe.ch/CODE) GPS卫星钟差文件
(30 s)CODE(ftp://ftp.aiub.unibe.ch/CODE) 地球自转参数文件 CODE(ftp://ftp.aiub.unibe.ch/CODE) Jason-3卫星精密轨道文件(1 min) IDS(https://ids-doris.org) SLR观测数据文件 NASA(https://cddis.nasa.gov/archive/slr) 表 3 载波相位残差RMS值汇总统计
mm 轨道 最小值 最大值 平均值 标准差 RMS 简化动力学 4.8 22.3 7.2 2.6 7.6 运动学 3.5 15.7 5.1 1.9 5.4 表 4 重叠轨道对比残差7天汇总统计结果
cm 轨道 轨道方向 最小值 最大值 平均值 标准差 RMS 简化动力学
轨道R −1.20 1.13 −0.02 0.32 0.32 T −4.07 1.79 0.05 0.97 0.97 N −1.33 1.27 0.14 0.53 0.55 运动学轨道 R −4.55 4.70 −0.02 1.12 1.12 T −4.92 4.42 −0.10 1.16 1.16 N −1.01 4.85 1.15 0.84 1.42 表 5 简化动力学轨道和运动学轨道分别与参考轨道对比7天汇总结果统计
cm 轨道 轨道方向 最小值 最大值 平均值 标准差 RMS 简化动力学
轨道R −12.81 7.07 −0.20 1.45 1.47 T −10.10 6.61 0.05 2.53 2.53 N −8.39 0.46 −2.95 1.21 3.19 运动学轨道 R −14.97 20.56 −0.30 4.35 4.36 T −16.41 20.43 −0.21 4.26 4.27 N −12.19 8.30 −2.18 2.75 3.51 表 6 SLR轨道检核7天汇总结果统计
cm 轨道 测站数 NP数 最小值 最大值 平均值 标准差 RMS 简化
动力学
轨道7 901 −3.18 3.23 0.82 0.69 2.02 运动学轨道 7 901 −0.84 8.29 −0.40 1.26 3.28 -
[1] DUMONT J P, ROSMORDUC V, CARRERE L, et al. Jason-3 products handbook[R/OL]. (2017-01-16)[2021-02-23]. https://www.nodc.noaa.gov/media/pdf/jasonz/j3_user_handbook.pdf
[2] 周旭华, 王晓慧, 赵罡, 等. HY2A卫星的GPS/DORIS/SLR数据精密定轨[J]. 武汉大学学报(信息科学版), 2015, 40(8): 1000-1005. [3] 郭金运, 黄金维, 胡建国, 等. 由星载GPS双差相位数据进行CHAMP卫星动力学定轨[J]. 武汉大学学报(信息科学版), 2006, 31(3): 213-217. [4] 张德成, 郑作亚, 刘娴, 等. 基于星载GPS数据的GRACE卫星动力学法定轨[J]. 全球定位系统, 2013, 38(5): 1-4. DOI: 10.3969/j.issn.1008-9268.2013.05.001 [5] YUNCK T P, BERTIGER W I, WU S C, et al. First assessment of GPS-based reduced dynamic orbit determination on TOPEX/Poseidon[J]. Geophysical research letters, 1994, 21(7): 541-544. DOI: 10.1029/94GL00010
[6] JÄGGI A, HUGENTOBLER U, BEUTLER G. Pseudo-stochastic orbit modeling techniques for low-earth orbiters[J]. Journal of geodesy, 2006(80): 47-60. DOI: 10.1007/s00190-006-0029-9
[7] HAINES B, BAR-SEVER Y, BERTIGER W, et al. One-centimeter orbit determination for Jason-1: new GPS-based strategies[J]. Marine geodesy, 2004, 27(1-2): 299-318. DOI: 10.1080/01490410490465300
[8] 秦建, 郭金运, 孔巧丽, 等. 基于星载GPS的CHAMP卫星精密简动力定轨[J]. 全球定位系统, 2011, 36(5): 41-45. DOI: 10.3969/j.issn.1008-9268.2011.05.010 [9] 秦建, 郭金运, 孔巧丽, 等. Jason-2卫星星载GPS数据cm级精密定轨[J]. 武汉大学学报(信息科学版), 2014, 39(2): 137-141. [10] 张德志, 孔巧丽, 张令纲. JASON-3卫星星载GPS厘米级精密定轨[J]. 测绘科学, 2020, 45(1): 42-47. [11] 杨洲铭, 郭金运, 夏要伟, 等. GRACE-FO卫星简化动力学精密定轨研究[J]. 地球物理学进展, 2020, 35(5): 1710-1716. [12] ZHOU M Y, LIU X, GUO J Y, et al. An enhanced method for detecting and repairing the cycle slips of dual-frequency onboard GPS receivers of LEO satellites[J]. Journal of sensors, 2020: 1-17. DOI: 10.1155/2020/8817626
[13] LIN H Q, GUO J Y, XIA Y W, et al. Effect of higher-order ionospheric delay on precise orbit determination of GRACE-FO based on satellite-borne GPS technique[J]. IEEE access, 2021(99): 29841-29849. DOI: 10.1109/ACCESS.2021.3059296
[14] 郑作亚. GPS数据预处理和星载GPS运动学定轨研究及其软件实现[D]. 上海: 上海天文台, 2004. [15] 张守建, 李建成, 邹贤才, 等. GRACE卫星非差运动学精密定轨分析[J]. 武汉大学学报(信息科学版), 2010, 35(6): 679-682. [16] 张兵兵, 牛继强, 王正涛, 等. Swarm系列卫星非差运动学厘米级精密定轨[J]. 测绘学报, 2021, 50(1): 27-36. [17] GUO J Y, QIN J, KONG Q L, et al. On simulation of precise orbit determination of HY-2 with centimeter precision based on satellite-borne GPS technique[J]. Applied geophysics, 2012, 9(1): 95-107. DOI: 10.1007/s11770-012-0319-3
[18] 夏要伟, 郭金运, 刘路, 等. 基于运动学和简化动力学的SWARM卫星精密定轨研究[J]. 大地测量与地球动力学, 2019, 39(4): 392-398. [19] DACH R, ANDRITSCH F, ARNOLD D, et al. Bernese GNSS software version 5.2[M]. Astronomical Institute, University of Bern, 2015. DOI: 10.7892/boris.72297.
[20] GUO J Y, HOU R, ZHOU M S, et al. Monitoring 2019 forest fires in southeastern australia with GNSS technique[J]. Remote sensing, 2021, 13(3): 386. DOI: 10.3390/rs13030386
[21] MONTENBRUCK O, GILL E. Satellite orbits: models, methods and applications[M/OL]. [2021-01-20]. The Observatory, 2001(121): 182. https://www.researchgate.net/profile/Eberhard-Gill-2/publication/234506679_Book_Review_Satellite_orbits_models_methods_and_applications_Springer_2000/links/54ddb8c80cf28a3d93fa2df2/Book-Review-Satellite-orbits-models-methods-and-applications-Springer-2000.pdf
[22] BOCK H, JAGGI A, MEYER U, et al. GPS-derived orbits for the GOCE satellite[J]. Journal of geodesy, 2011, 85(11): 807-818. DOI: 10.1007/s00190-011-0484-9
[23] 韩保民, 朱秀英, 柳林涛, 等. 伪随机脉冲估计及其在简化动力学定轨中的应用[J]. 武汉大学学报(信息科学版), 2007, 32(5): 466-469. [24] 赵春梅, 程鹏飞, 益鹏举. 基于伪随机脉冲估计的简化动力学卫星定轨方法[J]. 宇航学报, 2011(4): 762-766. DOI: 10.3873/j.issn.1000-1328.2011.04.009 [25] 吴显兵. 星载GPS低轨卫星几何法定轨及动力学平滑方法研究[D]. 郑州: 解放军信息工程大学, 2004. [26] 郭金运, 孔巧丽, 常晓涛, 等. 低轨卫星精密定轨理论与方法[M]. 北京: 测绘出版社, 2014: 130. [27] LIU M M, YUAN Y B, OU J K, et al. Research on attitude models and antenna phase center correction for Jason-3 satellite orbit determination[J]. Sensors, 2019, 19(10): 2408. DOI: 10.3390/s19102408
[28] 魏锦德, 黄张裕, 海美, 等. GPS天线相位中心误差的检测与改正[J]. 测绘科学技术学报, 2012, 29(6): 410-413, 417. [29] 胡志刚, 赵齐乐, 郭靖, 等. GPS天线相位中心校正对低轨卫星精密定轨的影响研究[J]. 测绘学报, 2011, 40(增刊): 34-38. [30] 周忠谟, 易杰军. GPS卫星测量原理与应用[M]. 北京: 测绘出版社, 1992. [31] GUO J Y, WANG Y C, SHEN Y, et al. Estimation of SLR station coordinates by means of SLR measurements to kinematic orbit of LEO satellites[J]. Earth planets and space, 2018, 70(1). DOI: 10.1186/s40623-018-0973-7
[32] XIA Y W, LIU X, GUO J Y, et al. On GPS data quality of GRACE-FO and GRACE satellites: effects of phase center variation and satellite attitude on precise orbit determination[J]. Acta geodaetica et geophysica, 2021(56): 93-111. DOI: 10.1007/s40328-020-00324-2
[33] 秦显平, 焦文海, 程芦颖, 等. 利用SLR检核CHAMP卫星轨道[J]. 武汉大学学报(信息科学版), 2005, 30(1): 38-41. -
期刊类型引用(1)
1. 张浩哲,常晓涛,朱广彬,刘伟,瞿庆亮. 资源三号03星星载GPS精密定轨与精度评价. 测绘科学. 2022(06): 38-43+89 .  百度学术
百度学术
其他类型引用(0)



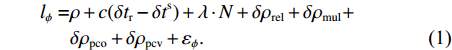
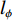
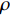
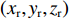
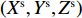
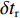
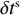
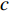
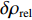
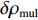
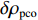
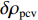
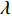
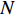
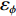
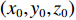
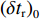
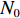
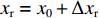
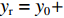
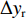
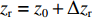
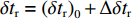
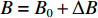
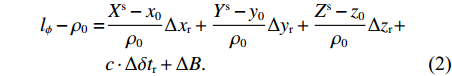

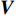
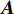
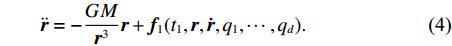
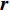
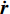
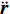
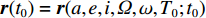
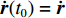
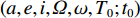
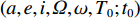
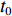
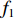
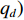
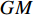
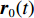
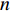
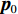
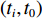
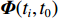
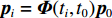
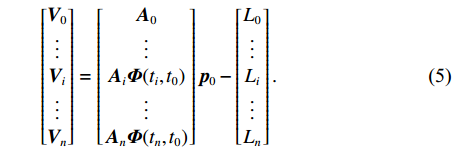
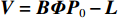
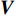
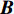
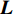
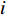
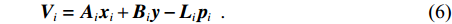
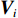
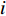
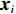
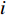
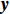
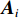
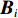
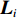
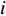
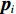
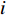
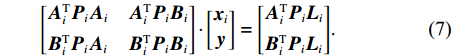
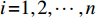
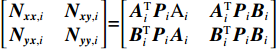
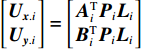
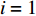
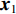
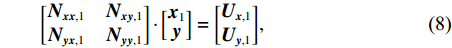
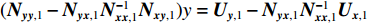
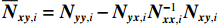
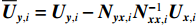

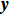
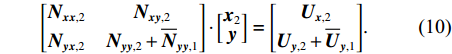
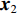
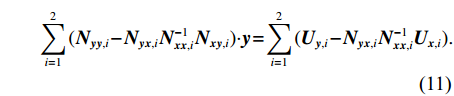
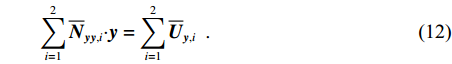
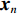
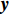
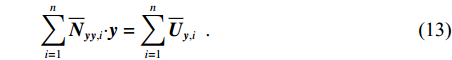
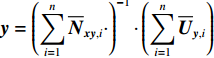
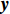
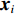

 下载:
下载: