A clock synchronization/calibration system combining EKF and LSTM neural networks
-
摘要: 本文研究了一种在卫星授时下,提高授时信号的授时精度和守时能力方法,即利用晶振计数器,记录下每个秒脉冲时刻的晶振频率信息;将记录历史信息输入到扩展卡尔曼滤波器(extended Kalman filter,EKF)中进行滤波,消除卫星秒脉冲信号的随机误差,提取北斗卫星前
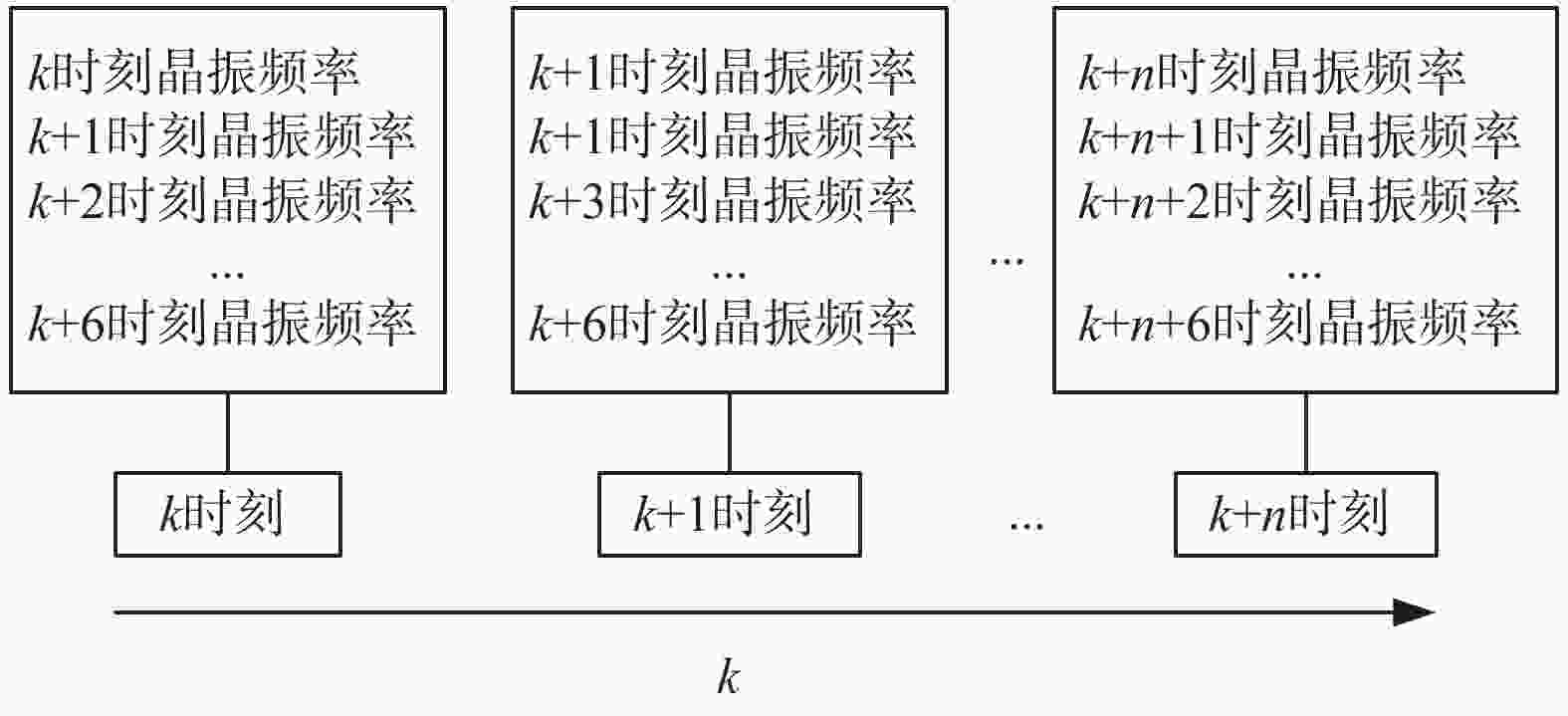
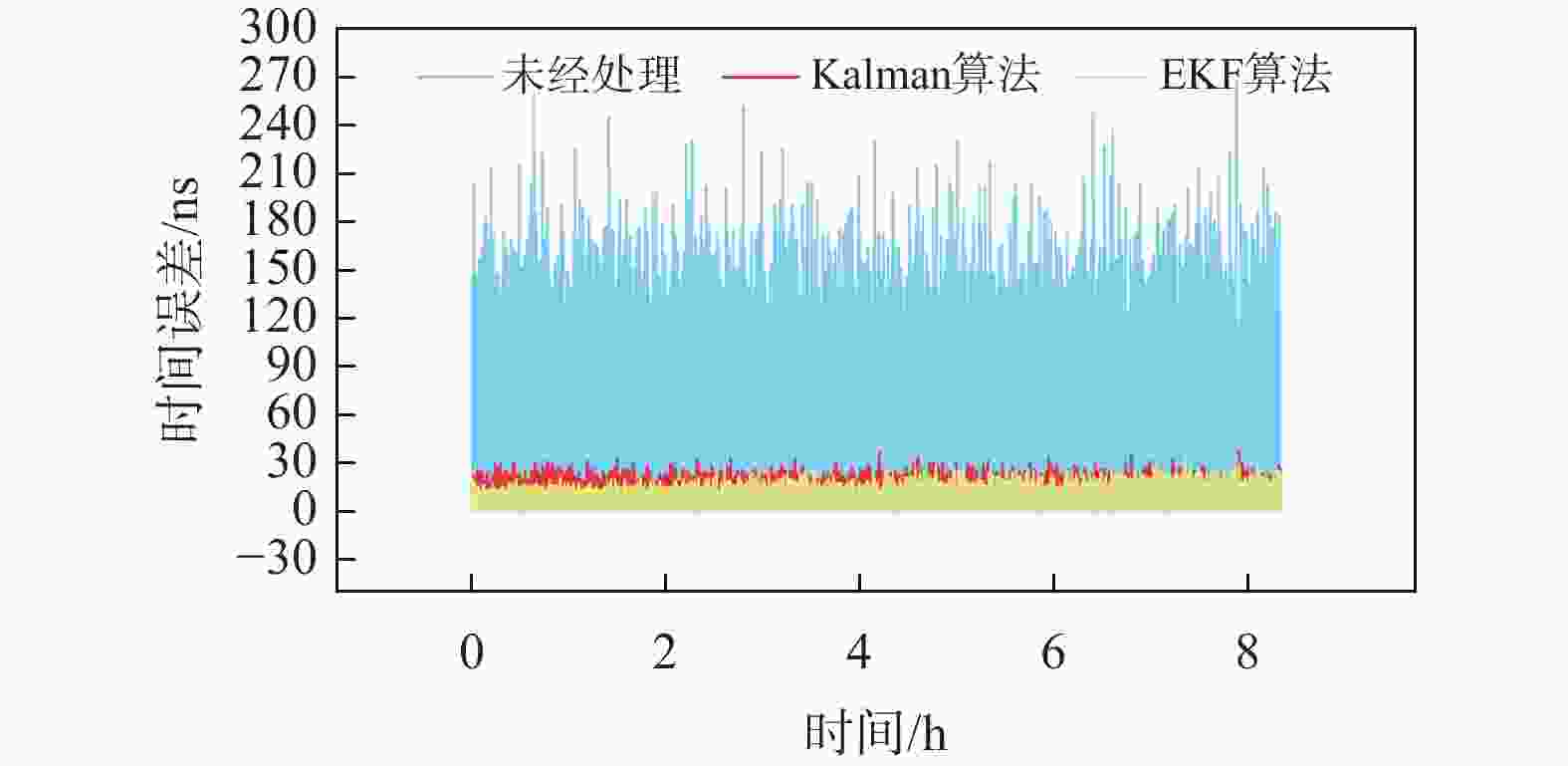
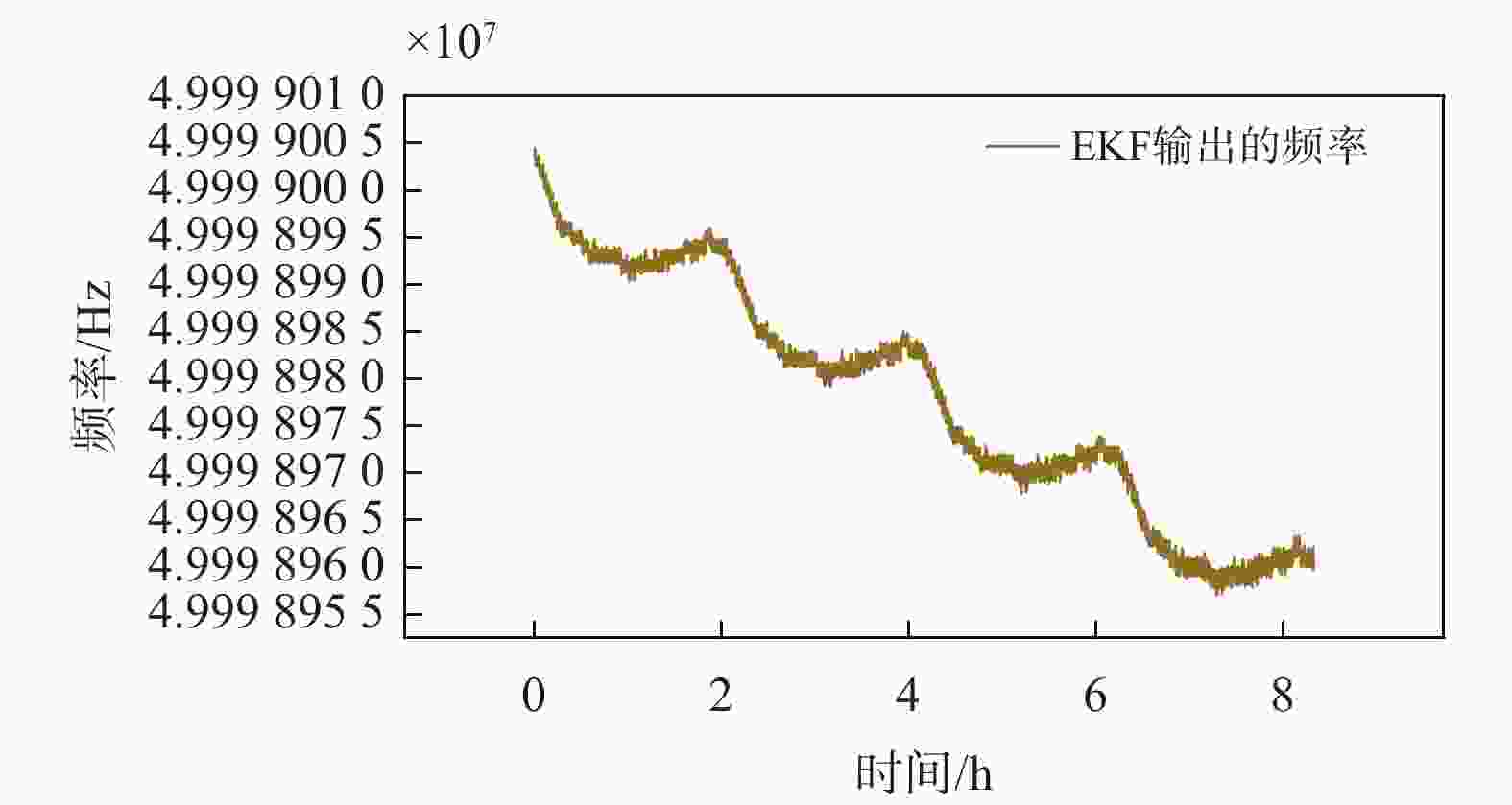
$N$ 秒秒脉冲的累计时间${t_{CN}}$ 、$k$ 时刻的晶振频率$fre(k)$ 、$k$ 时刻晶振变化速率$v(k)$ ;并将经过EKF输出的历史数据作为训练集,输入到长短期记忆 (long short-term memory,LSTM)神经网络中建立预测模型;通过控制变量法进行算法参数调试,找到最适合的预测模型. 试验结果表明:授时算法输出的授时信号精度最大误差为34 ns;授时算法8 h累计误差为1.001 μs,平均误差小于0.125 μs/h. 有效地提高了系统授时和守时精度.-
关键词:
- 扩展卡尔曼滤波(EKF) /
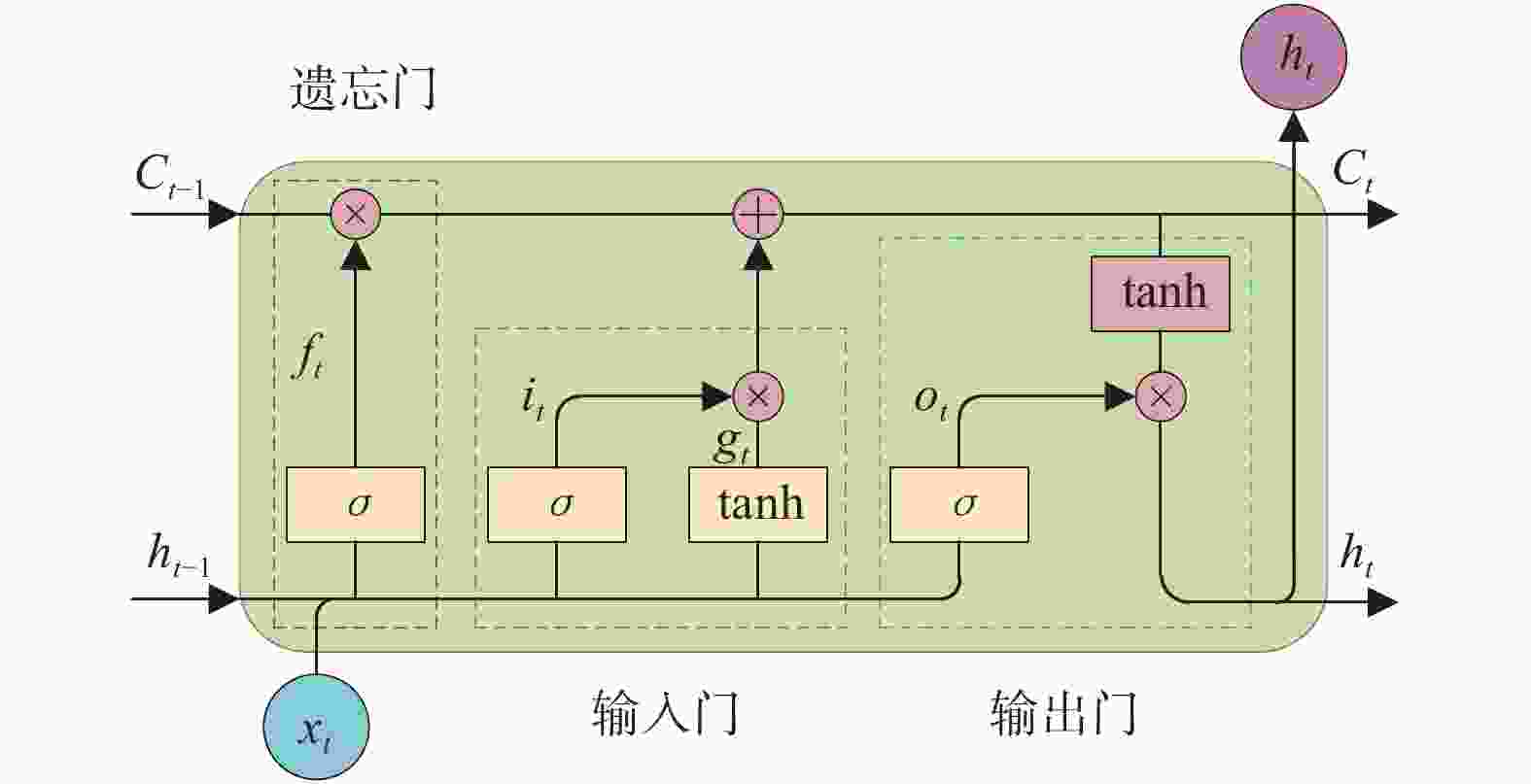
- 长短期记忆网络(LSTM) /
- 时间同步 /
- 卫星授时 /
- 晶振建模
Abstract: Research on methods to improve the timing accuracy and timekeeping capability of timing signals under satellite timing. By using a crystal oscillator counter, the crystal frequency information at the moment of each second pulse is recorded; the recorded historical information is input into an extended Kalman filter (EKF) for filtering, to eliminate the random error of the satellite second pulse signal, and extract the accumulated time of the first$N$ seconds of the BeiDou satellite pulse${t_{CN}}$ , and the crystal oscillator frequency$fre(k)$ at time$k$ ; and the crystal oscillator change rate$v(k)$ at time$k$ ; and the historical data output by the EKF is used as the training set, input into the long short-term memory (LSTM) network to establish a prediction model; the algorithm parameters are debugged using the control variable method to find the most suitable prediction model. The experimental results show that the maximum error of the timing signal output by the timing algorithm is 34 ns; the cumulative error of the timing algorithm in 8 hours is 1.001 μs, and the average error is less than 0.125 μs/h. This effectively improves the timing and timekeeping accuracy of the system. -
表 1 不同LSTM网络层单元数预测结果
LSTM网络层单元数 迭代次数 批次 特征数 8 h累计误差/μs 7 360 5000 7 6.723 8 360 5000 7 3.618 9 360 5000 7 1.001 10 360 5000 7 4.489 -
[1] 师伟国. 多路同步用北斗接口FPGA算法及实现[D]. 西安: 西安工业大学, 2023. [2] ALI S. Cybersecurity management for distributed control system: systematic approach[J]. Journal of ambient intelligence and humanized computing, 2021, 12(11): 10091-10103. DOI: 10.1007/s12652-020-02775-5 [3] KERO N, PUHM A, KERNEN T, et al. Performance and reliability aspects of clock synchronization techniques for industrial automation[J]. Proceedings of the IEEE, 2019, 107(6): 1011-1026. DOI: 10.1109/JPROC.2019.2915972 [4] 刘根友, 高铭, 尹翔飞, 等. 基于GNSS精密单点定位的高精度云平台授时[J]. 测绘学报, 2022, 51(8): 1736-1743. [5] 王井利, 佟晓宇, 张梅. 基于PSO-Elman神经网络BDS导航卫星钟差预报[J]. 全球定位系统, 2023, 48(2): 120-126. [6] 刘晓文. 基于LSTM的北斗三号卫星差分码偏差分析及预测[J]. 全球定位系统, 2024, 49(1): 102-107. [7] 胡安翼, 王登亮, 秦炳坤, 等. 基于TDOA辐射源定位系统架构设计[J/OL]. (2023-10-24)[2024-04-25]. 全球定位系统, 2023. [8] 肖再辉, 闫温合, 刘开琦, 等. eLoran噪声误差模型及产生方法研究[J]. 全球定位系统, 2022, 47(6): 73-78, 122. [9] 赖文彬, 李实锋. 基于DDS的BPM短波授时信号设计[J]. 全球定位系统, 2021, 46(4): 16-21. [10] 文超, 钟俊. 一种适用于GPS信号异常情况的高精度主时钟设计方法[J]. 电力系统保护与控制, 2016, 44(3): 103-108. [11] WANG G, XUE R, WANG J. A distributed maximum current ropy Kalman filter[J]. Signal processing, 2019, 160: 247-251. DOI: 10.1016/j.sigpro.2019.02.030 [12] 韩玉强. 智能电网卫星同步时钟的误差分析与修正方法研究[D]. 北京: 华北电力大学(北京), 2016. [13] 李依泽, 陆超, 王印峰, 等. 基于Kalman滤波与神经网络的高精度同步时钟算法[J]. 电网技术, 2019, 43(3): 777-784. [14] 倪子瞻, 罗颖婷, 江俊飞, 等. 基于自适应扩展卡尔曼滤波的变压器顶层油温多时间尺度预测[J]. (2023-12-27)[2024-03-12]. 电网技术. [15] HOCHREITER S, SCHMIDHUBER J. Long short-term memory[J]. Neural computation, 1997: 1735-1780. DOI: 10.1162/neco.1997.9.8.1735 [16] GRAVES A, MOHAMED A, HINTON G. Speech recognition with deep recurrent neural networks[C]//2013 IEEE International Conference on Acoustics, Speech and Signal Processing, 2013. DOI: 10.1109/ICASSP.2013.6638947 [17] 陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137. [18] 朱乔木, 李弘毅, 王子琪, 等. 基于长短期记忆网络的风电场发电功率超短期预测[J]. 电网技术, 2017, 41(12): 3797-3802. [19] 彭燕, 刘宇红, 张荣芬. 基于LSTM的股票价格预测建模与分析[J]. 计算机工程与应用, 2019, 55(11): 209-212. [20] 王晨, 李又轩, 吴其琦, 等. 基于SVM-STL-LSTM的区域短期电力负荷预测研究[J]. 水电能源科学, 2024, 42(4): 215-218. [21] 李泽文, 曾祥君, 黄智伟, 等. 基于高精度晶振的GPS秒时钟误差在线修正方法[J]. 电力系统自动化, 2006,30(13): 55-58. [22] 李泽文, 舒磊, 邓丰, 等. 基于全数字锁相环的电力系统高精度同步时钟[J]. 电力自动化设备, 2015, 35(7): 32-36. [23] 杨永标, 杨晓渝, 周捷. 利用FPGA实现GPS失步下精确守时[J]. 电力自动化设备, 2007, 2(7): 109-112. -















 下载:
下载: